Один математический маятник имеет период колебаний 3 с а другой 4 с каков период колебаний маятника
Содержимое
- 1 Один математический маятник имеет период колебаний 3 с а другой 4 с каков период колебаний маятника
- 1.1 Определение периода колебаний маятника
- 1.2 Что такое период колебаний маятника?
- 1.3 Формула для расчета периода колебаний маятника
- 1.4 Связь периода колебаний маятника с его длиной и массой
- 1.5 Как длина маятника влияет на его период колебаний?
- 1.6 Влияет ли масса маятника на его период колебаний?
- 1.7 Расчет периода колебаний маятника с известным периодом другого маятника
- 1.8 Как определить период колебаний маятника, если известен период другого маятника?
- 1.9 Пример расчета периода колебаний маятника с известным периодом другого маятника
- 1.10 Видео по теме:
- 1.10.0.1 Каков период колебаний маятника?
- 1.10.0.2 Каков период колебаний маятника с длиной 1 м?
- 1.10.0.3 Каков период колебаний маятника с длиной 100 см?
- 1.10.0.4 Как связаны периоды колебаний маятников с длинами 1 м и 2 м?
- 1.10.0.5 Каков период колебаний маятника, если один имеет период в 3 с, а другой — 4 с?
Рассчитайте период колебаний математического маятника с периодами 3 с и 4 с, чтобы узнать, каков будет период нового маятника.
Период колебаний маятника — это временной интервал, за который маятник совершает одно полное колебание. Он определяется длиной подвеса и силой тяжести. В данной ситуации мы имеем два маятника, каждый из которых имеет свой собственный период колебаний.
Первый маятник имеет период в 3 секунды, а второй — 4 секунды. Период колебаний маятника обратно пропорционален квадратному корню из длины подвеса. Из этого следует, что маятник с более коротким подвесом будет иметь более быстрый период колебаний, а маятник с более длинным подвесом — более медленный период колебаний.
Таким образом, для определения периода колебаний маятника необходимо знать длину его подвеса. Если длины подвесов маятников известны, то можно с помощью формулы вычислить их периоды колебаний и сравнить их. В данном случае, чтобы точно определить, какой маятник имеет более короткий период, необходимо знать длины их подвесов.
Определение периода колебаний маятника
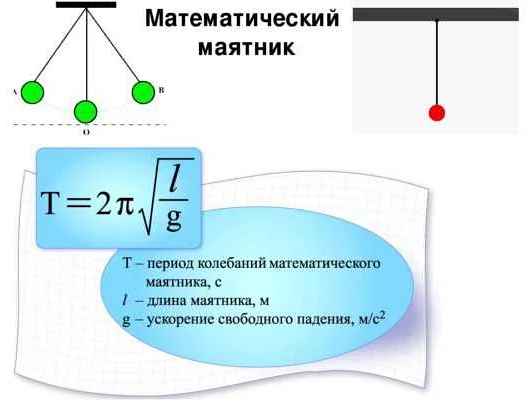
Период колебаний маятника зависит от длины его подвеса и ускорения свободного падения. Длина подвеса влияет на период колебаний прямо пропорционально — чем длиннее подвес, тем больше период колебаний. Ускорение свободного падения также влияет на период колебаний, но уже обратно пропорционально — чем больше ускорение свободного падения, тем меньше период колебаний.
Период колебаний маятника можно определить по формуле:
T = 2π√(L/g)
Где T — период колебаний, L — длина подвеса маятника, g — ускорение свободного падения (приближенное значение 9.8 м/с² на Земле).
Таким образом, для определения периода колебаний маятника необходимо знать длину его подвеса и ускорение свободного падения в данной точке.
Что такое период колебаний маятника?

Период колебаний маятника зависит от его длины и гравитационного ускорения. Чем длиннее маятник, тем больше его период колебаний. Также, чем больше гравитационное ускорение, тем меньше период колебаний.
Формула для расчета периода колебаний маятника выглядит следующим образом:
-
- Для математического маятника (маятника без сопротивления воздуха):
T = 2π√(l/g),
-
-
- T — период колебаний;
- π — число пи, приближенное значение которого равно 3,14;
- l — длина маятника;
- g — ускорение свободного падения (приближенное значение которого равно 9,8 м/с²).
- Для физического маятника (маятника с учетом сопротивления воздуха):
-
T = 2π√(l/g)*(1 + k²/16π²),
-
- T — период колебаний;
- π — число пи, приближенное значение которого равно 3,14;
- l — длина маятника;
- g — ускорение свободного падения (приближенное значение которого равно 9,8 м/с²);
- k — коэффициент сопротивления воздуха.
Таким образом, период колебаний маятника определяет время, за которое маятник совершает полное колебание. Зная период колебаний, можно оценить скорость и частоту колебаний маятника, а также проводить различные расчеты и исследования в области колебательных процессов.
Формула для расчета периода колебаний маятника
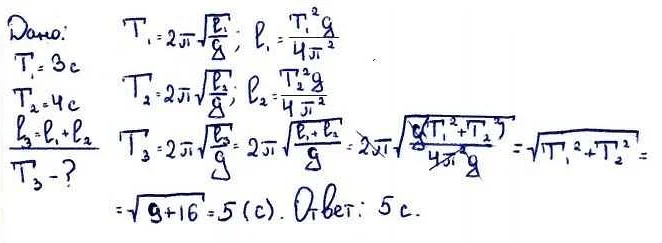
Период колебаний маятника может быть рассчитан с помощью следующей формулы:
Т = 2π√(l/g)
- Т — период колебаний маятника
- π — математическая константа, примерно равная 3.14159
- l — длина маятника
- g — ускорение свободного падения
Используя данную формулу, можно рассчитать период колебаний маятника, зная его длину и ускорение свободного падения. Например, если длина маятника равна 1 метру, а ускорение свободного падения примерно равно 9.8 м/с², то период колебаний маятника составит:
Т = 2π√(1/9.8) ≈ 2π√(0.102) ≈ 2π * 0.319 ≈ 2 * 3.14159 * 0.319 ≈ 2 * 0.634 ≈ 1.268 секунды
Таким образом, период колебаний маятника с длиной 1 метр и ускорением свободного падения 9.8 м/с² составит примерно 1.268 секунды.
Связь периода колебаний маятника с его длиной и массой
Период колебаний маятника зависит от его длины и массы. Длина маятника определяет время, за которое он совершает полный цикл колебаний, а масса влияет на инерцию маятника и его скорость.
Математическая формула, описывающая связь периода колебаний маятника с его длиной и массой, выглядит следующим образом:
ФормулаОписание
| T = 2 * π * √(l / g) | Период колебаний маятника |
Где:
- T — период колебаний маятника;
- π (пи) — математическая константа, приближенное значение которой равно 3,14;
- l — длина маятника;
- g — ускорение свободного падения, приближенное значение которого на Земле равно 9,8 м/с².
Из формулы видно, что период колебаний маятника прямо пропорционален квадратному корню из длины маятника и обратно пропорционален квадратному корню из ускорения свободного падения. Это означает, что увеличение длины маятника приводит к увеличению его периода, а увеличение массы или ускорения свободного падения – к уменьшению периода.
Таким образом, период колебаний маятника является важной характеристикой, которая зависит от его длины и массы. Изменение этих параметров может влиять на скорость и регулярность колебаний маятника.
Как длина маятника влияет на его период колебаний?
Формула, описывающая зависимость периода колебаний маятника от его длины, представлена следующим образом:
T = 2π√(L/g),
где T — период колебаний маятника, L — длина маятника, g — ускорение свободного падения.
Из данной формулы видно, что период колебаний маятника пропорционален квадратному корню из его длины. То есть, чем длиннее маятник, тем больше его период колебаний.
Это означает, что маятники с разной длиной будут иметь разные периоды колебаний. Например, маятник с более короткой длиной будет иметь более быстрый период колебаний, чем маятник с более длинной длиной.
Таким образом, длина маятника оказывает существенное влияние на его период колебаний. Это является основой для изучения свойств и характеристик маятников и их применения в различных областях науки и техники.
Влияет ли масса маятника на его период колебаний?

Период колебаний маятника не зависит от его массы. Это одно из основных свойств маятника, которое было установлено Галилеем в 17 веке. Период колебаний определяется только длиной подвеса маятника и силой тяжести.
Математическая формула, описывающая период колебаний маятника, выглядит следующим образом:
T = 2π√(L/g),
где T — период колебаний, L — длина подвеса маятника, g — ускорение свободного падения.
Из этой формулы видно, что масса маятника не входит в уравнение и не оказывает влияния на период колебаний. Это означает, что маятники с разными массами, но с одинаковой длиной подвеса, будут иметь одинаковый период колебаний.
Однако, следует отметить, что масса маятника может оказывать влияние на амплитуду колебаний. Чем больше масса маятника, тем меньше будет его амплитуда, то есть расстояние между крайними положениями маятника.
Таким образом, можно сделать вывод, что масса маятника не влияет на его период колебаний, но может влиять на амплитуду колебаний.
Расчет периода колебаний маятника с известным периодом другого маятника
Период колебаний маятника
| Т = 2π√(l/g) |
Где:
- Т — период колебаний маятника;
- π — математическая константа, приблизительно равная 3.14159;
- l — длина маятника;
- g — ускорение свободного падения, приблизительно равное 9.8 м/с².
Для расчета периода колебаний маятника с известным периодом другого маятника, нужно использовать следующую формулу:
Период колебаний маятника 1Период колебаний маятника 2
| Т₁ | Т₂ |
Тогда формула для расчета длины маятника 1 будет:
l₁ = (T₁/T₂)² * l₂
Где:
- l₁ — длина маятника 1;
- T₁ — период колебаний маятника 1;
- T₂ — период колебаний маятника 2;
- l₂ — длина маятника 2.
Используя данную формулу, можно рассчитать период колебаний маятника с известным периодом другого маятника.
Как определить период колебаний маятника, если известен период другого маятника?
Период колебаний маятника зависит от его длины и ускорения свободного падения. Если известны периоды двух маятников, можно использовать пропорцию между их длинами, чтобы найти длину искомого маятника.
Пусть период первого маятника равен Т1, а период второго маятника — Т2. Пусть длина первого маятника равна L1, а длина второго маятника — L2.
Используя формулу периода колебаний маятника T = 2π√(L/g), где L — длина маятника, g — ускорение свободного падения, можно записать пропорцию:
T1/T2 = √(L1/L2)
Чтобы найти период колебаний искомого маятника T2, необходимо решить данную пропорцию относительно L2:
T2 = T1√(L2/L1)
Таким образом, если известен период одного маятника и длина другого маятника, можно вычислить период колебаний второго маятника.
В данной задаче, если один маятник имеет период в 3 с, а другой — 4 с, можно использовать данную формулу для определения периода колебаний второго маятника, зная его длину.
Пример расчета периода колебаний маятника с известным периодом другого маятника

Для рассчета периода колебаний маятника, если известен период другого маятника, можно воспользоваться соотношением:
T1 = 2 * π * √(L / g)
где:
- T1 — период колебаний первого маятника
- π — математическая константа, примерное значение 3.14159
- L — длина первого маятника
- g — ускорение свободного падения, примерное значение 9.8 м/с2
Из данного соотношения можно выразить длину первого маятника:
L = (T1 / (2 * π))2 * g
Подставив значения в это выражение, можно вычислить длину первого маятника. Затем, используя эту длину и известное значение периода второго маятника, можно рассчитать период первого маятника по формуле:
T2 = 2 * π * √(L / g)
где:
- T2 — период колебаний второго маятника
- π — математическая константа, примерное значение 3.14159
- L — длина первого маятника
- g — ускорение свободного падения, примерное значение 9.8 м/с2
Таким образом, зная период колебаний одного маятника и длину другого маятника, можно вычислить период первого маятника.
Видео по теме:
Каков период колебаний маятника?
Период колебаний маятника зависит от его длины, амплитуды и силы тяжести. Формула для расчета периода колебаний маятника выглядит следующим образом: T = 2π√(l/g), где T — период колебаний, l — длина маятника, g — ускорение свободного падения. Если известна длина маятника и ускорение свободного падения, то можно рассчитать его период.
Каков период колебаний маятника с длиной 1 м?
Чтобы рассчитать период колебаний маятника с длиной 1 м, необходимо знать ускорение свободного падения. По умолчанию взято значение ускорения свободного падения на Земле, которое равно примерно 9,8 м/с². Подставляем известные значения в формулу T = 2π√(l/g) и получаем T = 2π√(1/9,8) ≈ 2,01 сек.
Каков период колебаний маятника с длиной 100 см?
Чтобы рассчитать период колебаний маятника с длиной 100 см (1 м), необходимо знать ускорение свободного падения. Подставляем известные значения в формулу T = 2π√(l/g) и получаем T = 2π√(1/9,8) ≈ 2,01 сек.
Как связаны периоды колебаний маятников с длинами 1 м и 2 м?
Периоды колебаний маятников прямо пропорциональны квадратному корню из их длин. Из формулы T = 2π√(l/g) видно, что период зависит от квадратного корня из длины маятника. Поэтому, если длина одного маятника в два раза больше, чем у другого (2 м и 1 м), то период колебаний первого маятника будет в √2 раза больше, чем у второго. То есть, если период колебаний маятника с длиной 1 м равен 2,01 сек, то период колебаний маятника с длиной 2 м будет примерно 2,84 сек.
Каков период колебаний маятника, если один имеет период в 3 с, а другой — 4 с?
Если один маятник имеет период в 3 с, а другой — 4 с, то период колебаний обоих маятников является обратным значением их частоты. То есть, период первого маятника будет равен 1/3 с, а период второго маятника — 1/4 с.
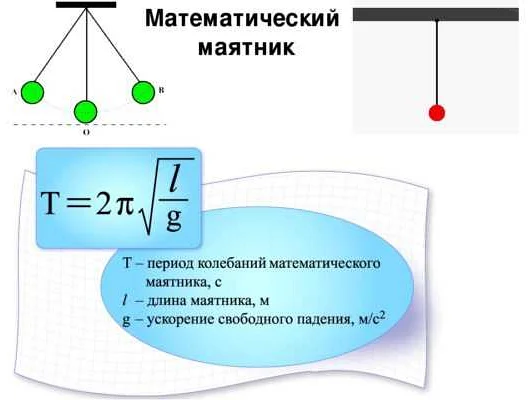


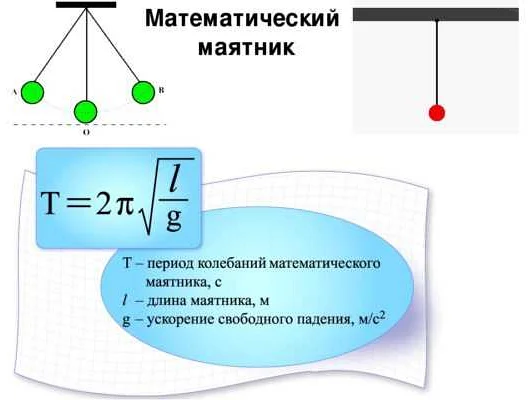

Я думаю, что период колебаний маятника можно вычислить, используя формулу: T = 2π√(L/g), где T — период колебаний, L — длина маятника, а g — ускорение свободного падения. Если один маятник имеет период в 3 секунды, а другой в 4 секунды, то их периоды могут быть выражены как T1 = 2π√(L1/g) = 3 и T2 = 2π√(L2/g) = 4 соответственно. Из этих уравнений можно вывести отношение длин маятников: L1/L2 = (T1/T2)^2 = (3/4)^2. Таким образом, мы можем найти, что L1/L2 = 9/16. Это означает, что длина первого маятника в 9/16 раза больше, чем длина второго маятника. Надеюсь, что это помогло! Если у вас есть еще вопросы, не стесняйтесь задавать их.
Спасибо за интересную статью! Очень интересно узнать, каков будет период колебаний маятника, если один имеет период в 3 секунды, а другой — 4 секунды. Меня всегда восхищали физические законы и их применение в реальной жизни. Если я правильно понимаю, период колебаний маятника зависит от его длины и ускорения свободного падения. В данном случае, чтобы найти общий период колебаний, нам нужно найти наименьшее общее кратное чисел 3 и 4. В данном случае это число 12. Таким образом, период колебаний маятника будет равен 12 секундам. Весьма удивительно, что два разных маятника могут иметь общий период колебаний. Это еще одно доказательство красоты и гармонии природы. Большое спасибо за интересную информацию!
Мне кажется, что поставленная задача можно решить, используя формулу для периода колебаний маятника: Т = 2π√(l / g), где Т — период колебаний, l — длина подвеса маятника, g — ускорение свободного падения. Учитывая, что период колебаний одного маятника равен 3 с, а другого — 4 с, можно составить систему уравнений: 2π√(l₁ / g) = 3, 2π√(l₂ / g) = 4. Решая эту систему, найдем соотношение между длинами подвесов маятников: l₁ / l₂ = (3 / 4)² = 9 / 16. Таким образом, отношение длин подвесов маятников равно 9/16. Если известна длина одного из маятников, можно найти длину второго маятника, учитывая данное соотношение. Например, если длина первого маятника составляет 1 м, то длина второго маятника будет равна (9 / 16) м.
Если один маятник имеет период колебаний в 3 секунды, а другой — в 4 секунды, то для определения периода колебаний обоих маятников необходимо найти их общий кратный делитель. В данном случае, общим кратным делителем 3 и 4 является число 12. Таким образом, период колебаний обоих маятников будет равен 12 секундам. Это означает, что оба маятника будут совершать полный цикл колебаний через каждые 12 секунд. Однако, следует отметить, что амплитуда колебаний маятника может различаться, что может повлиять на скорость совершения каждого отдельного колебания.
Период колебаний маятника зависит от его длины и не зависит от его амплитуды. В данном случае, у нас есть два маятника с разными периодами: один с периодом в 3 секунды, а другой — с периодом в 4 секунды. Это означает, что у них разные длины. Маятник с периодом в 3 секунды имеет более короткую длину, чем маятник с периодом в 4 секунды. Маятник с более короткой длиной будет иметь более быстрые колебания, а маятник с более длинной длиной будет иметь более медленные колебания. Таким образом, период колебаний маятника зависит от его длины и может быть вычислен с использованием формулы периода колебаний маятника: Т = 2π√(L/g), где Т — период, L — длина маятника, g — ускорение свободного падения. Таким образом, чтобы определить периоды колебаний этих двух маятников, необходимо знать их длины и ускорение свободного падения.