Что такое функционал в математике

Функционал в математике — это понятие, которое описывает определенную математическую функцию или операцию. Он используется для анализа и описания различных свойств и поведения функций. В данной статье мы рассмотрим, что такое функционал, его основные свойства и примеры применения в различных областях математики.

В математике функционал – это понятие, которое играет важную роль в анализе и функциональном анализе. Функционал – это отображение из некоторого векторного пространства в поле скаляров. Он принимает вектор и возвращает скаляр. Таким образом, функционал устанавливает соответствие между векторами и скалярами.

Функционалы имеют ряд свойств, которые являются основополагающими для их изучения и применения. Во-первых, функционал линеен, то есть удовлетворяет условию линейности: f(x + y) = f(x) + f(y) и f(ax) = af(x), где x и y – векторы, а a – скаляр. Во-вторых, функционал ограничен, если существует такая константа C, что |f(x)| ≤ C·||x|| для всех векторов x. В-третьих, функционал непрерывен, если при малом изменении вектора x меняется только значение функционала f(x).

Примеры функционалов включают в себя скалярное произведение, интегралы, линейные операторы и многое другое. Например, скалярное произведение является функционалом, который принимает два вектора и возвращает их скалярное произведение. Интегралы – это функционалы, которые принимают функции и возвращают их интегралы.

Функционалы являются мощным инструментом в математическом анализе и функциональном анализе. Они используются для решения различных задач, таких как нахождение экстремумов функций, решение дифференциальных уравнений, определение сходимости и др. Понимание функционалов и их свойств позволяет математикам и инженерам эффективно и точно решать задачи в различных областях науки и техники.

Определение функционала

Функционалом является также отображение, которое принимает функцию в качестве аргумента и возвращает число в качестве значения. Такая функция может быть определена на конечномерном или бесконечномерном пространстве функций.

Функционалы играют важную роль в различных областях математики и естественных науках. Они позволяют изучать свойства функций, оценивать их поведение, а также решать различные задачи оптимизации и вариационного исчисления.

Примеры функционалов включают интегралы, скалярные произведения, нормы и многое другое.

Свойства функционала

У функционалов есть несколько важных свойств:

СвойствоОписание

Аддитивность	Если функционал F(f+g) равен сумме функционалов F(f) и F(g), то он называется аддитивным.
Однородность	Если функционал F(af) равен произведению числа a и функционала F(f), то он называется однородным.
Монотонность	Если для любых двух функций f и g, таких что f(x) ≤ g(x) для всех x, функционал F(f) ≤ F(g), то он называется монотонным.
Ограниченность	Если для всех функций f, существуют числа m и M, такие что m ≤ F(f) ≤ M, то функционал называется ограниченным.

Эти свойства позволяют нам рассматривать функционалы как аналоги операций в линейной алгебре, таких как сумма, умножение на число и сравнение. Они также позволяют нам делать выводы о функциях на основе значений функционалов.

Функционал в анализе

Функционалы могут быть заданы различными способами, например, через интегралы, производные или конечные разности. Они позволяют изучать свойства функций и находить оптимальные решения задач.

Основные свойства функционалов включают линейность, ограниченность и непрерывность. Линейность означает, что функционал обладает свойством суперпозиции, то есть F(k*f) = k*F(f), где k — произвольная константа. Ограниченность означает, что функционал ограничен сверху и снизу. Непрерывность означает, что функционал сохраняет пределы последовательностей функций.

Примеры функционалов в анализе включают функционалы Фреше-Рисса, Лагранжа и Эйлера. Функционалы Фреше-Рисса используются для изучения гладкости и дифференцируемости функций. Функционалы Лагранжа и Эйлера широко применяются в вариационном исчислении для нахождения экстремалей функционалов.

Примеры функционалов

1. Функционал на множестве действительных чисел:

Рассмотрим функцию f(x) = x^2. Она является примером функционала на множестве действительных чисел, так как каждому числу x ставит в соответствие число x^2. Функционал f можно определить для любого действительного числа и он будет возвращать его квадрат.

2. Функционал на множестве векторов:

Пусть V — линейное пространство векторов. Тогда можно рассмотреть функционал на V, который каждому вектору x из V ставит в соответствие его длину или норму. Такой функционал обычно обозначается как ||x||.

3. Функционал на множестве функций:

Рассмотрим функцию f(x) = ∫[0, x] g(t) dt, где g(t) — заданная функция. Эта функция является примером функционала на множестве функций, так как она каждой функции g(t) ставит в соответствие число, которое равно интегралу функции g(t) на интервале [0, x]. Функционал f можно определить для любой функции и он будет возвращать это число.

4. Функционал на множестве последовательностей:

Рассмотрим функцию f(x) = limn→∞ xn, где x = {xn} — заданная последовательность. Эта функция является примером функционала на множестве последовательностей, так как она каждой последовательности x = {xn} ставит в соответствие число, которое является пределом этой последовательности. Функционал f можно определить для любой последовательности и он будет возвращать ее предел.

Линейный функционал

Аддитивность означает, что если мы подаем на вход линейного функционала сумму двух векторов, то результат будет равен сумме значений функционала для этих векторов.

Однородность означает, что если мы подаем на вход линейного функционала вектор, умноженный на скаляр, то результат будет равен значению функционала для исходного вектора, умноженного на этот скаляр.

Линейные функционалы широко используются в математике и физике. Они позволяют описывать и анализировать различные физические явления и процессы.

Примерами линейных функционалов могут служить функции, выражающие энергию, массу, момент импульса и другие физические величины. Они принимают векторы, описывающие состояние системы, и возвращают числа, характеризующие эти состояния.

Линейные функционалы также используются в линейной алгебре для решения систем линейных уравнений и нахождения собственных значений и собственных векторов матриц.

Конечномерные функциональные пространства

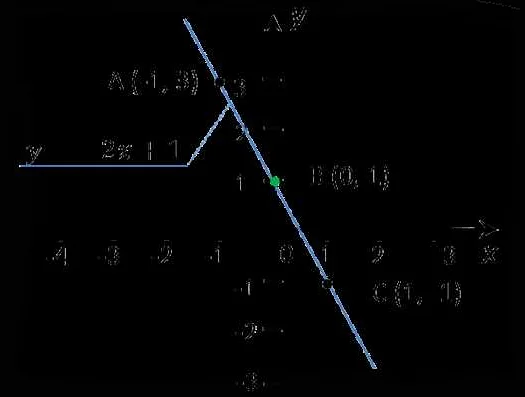
Одним из примеров конечномерного функционального пространства является пространство полиномов степени не выше n. В этом пространстве каждая функция представляется в виде полинома, где n – максимальная степень полинома. Пространство полиномов степени не выше n имеет размерность n+1, так как существует n+1 различных базисных полиномов: 1, x, x^2, …, x^n.

В конечномерных функциональных пространствах можно определить операции сложения и умножения на число, которые сохраняются с точностью до размерности пространства. Также такие пространства обладают свойством замкнутости относительно операций сложения и умножения на число.

Конечномерные функциональные пространства находят широкое применение в различных областях математики и физики. Они являются основой для построения различных аппроксимационных методов и численных методов решения уравнений.

Видео по теме:

Вопрос-ответ:

Что такое функционал в математике?

Функционал в математике — это отображение из пространства функций в числовое поле. Он сопоставляет каждой функции из заданного множества число.

Какие свойства имеют функционалы в математике?

Функционалы в математике обладают рядом важных свойств. Они линейны, то есть удовлетворяют свойству суперпозиции и однородности. Кроме того, функционалы могут быть ограниченными или неограниченными и непрерывными или разрывными.

Какие примеры функционалов в математике можно привести?

Примеры функционалов в математике включают интегралы, дифференциалы и линейные функции. Например, интеграл Лебега является функционалом, который сопоставляет функции их интегралы. Дифференциал является функционалом, который сопоставляет функции их производные. Линейная функция сопоставляет каждой функции ее значение в заданной точке.

Чем отличается ограниченный функционал от неограниченного?

Ограниченный функционал — это функционал, который имеет конечное значение на каждой функции из заданного множества. Неограниченный функционал — это функционал, который может иметь бесконечное значение на некоторых функциях.

Какие свойства имеют непрерывные функционалы?

Непрерывный функционал — это функционал, который сохраняет пределы. Если последовательность функций сходится к функции, то непрерывный функционал сохраняет пределы этой последовательности. Это важное свойство, которое позволяет работать с функционалами в математическом анализе.

Что такое функционал в математике?

Функционал в математике — это отображение, которое сопоставляет элементам некоторого множества некоторые значения или объекты. В более простых словах, функционал — это правило, которое ставит в соответствие элементам одного множества элементы другого множества.

Какие свойства имеет функционал в математике?

Функционал в математике обладает несколькими важными свойствами. Во-первых, он должен быть линейным, то есть сохранять операцию сложения и умножения на число. Во-вторых, функционал может быть непрерывным или ограниченным. Также функционал может быть выпуклым или вогнутым. Наконец, функционал может быть дифференцируемым или интегрируемым.

Пространство обобщенных функций

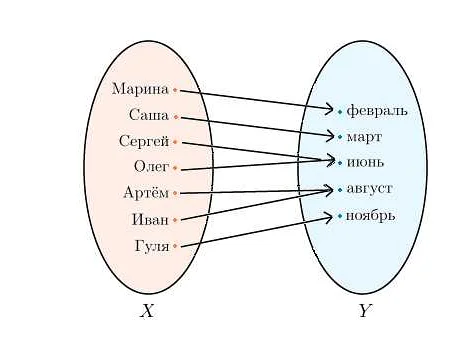
Пространство обобщенных функций обладает рядом важных свойств. Оно является линейным пространством, то есть сумма и умножение на число обобщенных функций дают новую обобщенную функцию. Также пространство обобщенных функций обладает топологией, которая позволяет определить сходимость последовательностей обобщенных функций.

Примеры обобщенных функций включают в себя дельта-функцию Дирака, ступенчатую функцию Хевисайда и функцию Дирихле. Дельта-функция Дирака является дискретной обобщенной функцией, которая имеет значение бесконечности в точке 0 и ноль во всех остальных точках. Ступенчатая функция Хевисайда равна нулю до точки 0 и единице после этой точки. Функция Дирихле является периодической функцией, которая принимает значение 1 на множестве рациональных чисел и значение 0 на множестве иррациональных чисел.

Пространство обобщенных функций играет важную роль в различных областях математики и физики. Оно позволяет обобщить понятие функции и решать уравнения с помощью распределений. Пространство обобщенных функций также используется в теории распределений и математической физике.

Применение функционала в науке и технике

В науке функционал используется для описания различных систем и процессов. Например, в физике функционал может быть использован для описания движения частиц, электромагнитного поля или квантовых систем. В биологии функционал может быть применен для моделирования биологических процессов, таких как рост клеток или эволюция организмов.

В технике функционал широко используется для проектирования и оптимизации различных систем. Например, функционал может быть использован для оптимизации формы крыла самолета, распределения материалов в конструкции или управления роботами.

Применение функционала в науке и технике позволяет решать разнообразные задачи. Например, оптимизация функционала может помочь найти наилучшие решения при ограниченных ресурсах или условиях. Моделирование функционала позволяет изучать и анализировать разнообразные системы и процессы, что является важным для развития науки и техники.

Таким образом, функционал играет важную роль в науке и технике, позволяя формализовать, изучать и оптимизировать различные системы и процессы. Применение функционала дает возможность решать сложные задачи и получать полезные результаты, способствуя развитию науки и техники.