Что такое математическая модель и как ее использовать: 10 примеров

Статья расскажет о том, что представляет собой математическая модель, как она создается и используется, а также примеры применения математических моделей в реальной жизни. Познакомьтесь с основами моделирования и попробуйте создать свою собственную математическую модель.

Математическая модель — это формальное описание объекта или явления, основанное на математических методах. Моделирование является важным инструментом в науке, инженерии, экономике и других областях, позволяя изучать поведение системы и прогнозировать ее будущее.

Создание математической модели включает в себя различные шаги, от анализа данных до выбора подходящих математических методов. В этой статье мы рассмотрим 10 примеров математических моделей в различных областях и опишем процесс их создания.

Вы узнаете, как создавать модели экономических систем, популяционных динамик, физических явлений, а также моделировать проблемы, связанные с транспортом, энергетикой и многим другим. В конце статьи вы получите ценные советы по созданию собственной математической модели.

Что такое математическая модель?

Математическая модель — это абстрактное описание какого-либо явления или процесса, представленное в математической форме. Она позволяет описывать, анализировать и предсказывать поведение системы или процесса.

Математическая модель может быть создана для различных областей знания, например, в экономике, физике, биологии, социологии и т.д. Она может быть простой или сложной, в зависимости от того, насколько подробно описывается система.

Математическая модель имеет свои особенности. Во-первых, она не является полным описанием реального мира, а лишь его упрощенной моделью. Во-вторых, ее правильность зависит от правильности выбора параметров и начальных условий.

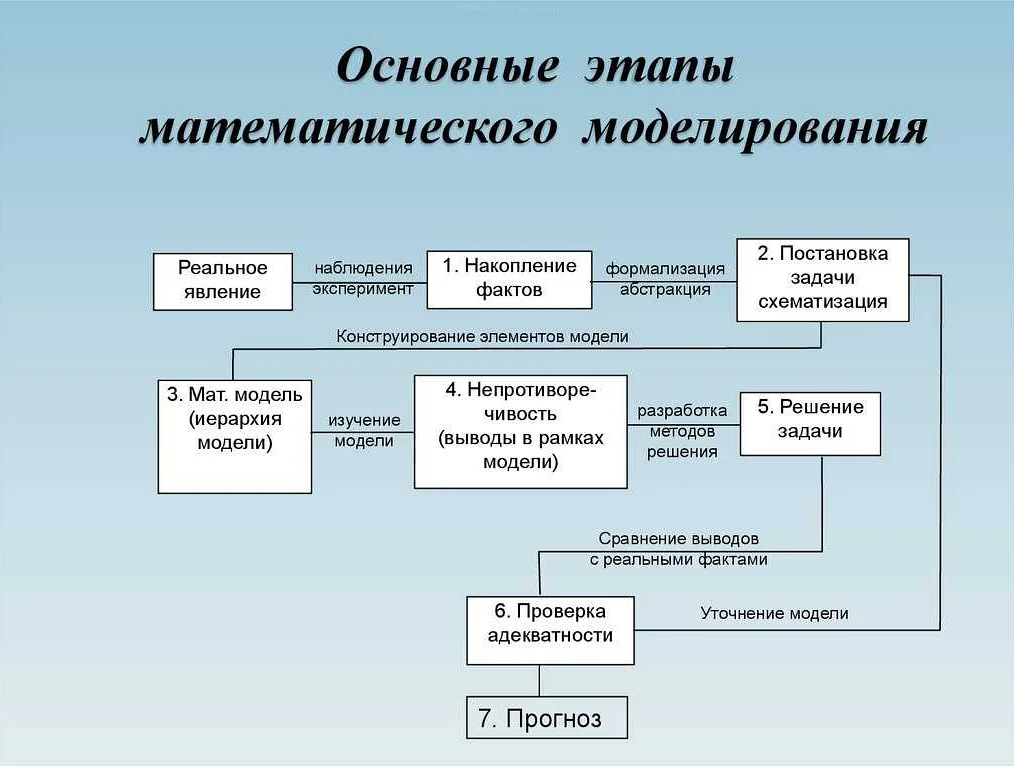
В создании математической модели различают несколько этапов. На первом этапе необходимо определить, что именно будет моделироваться и каковы ее цели. Затем на основе эмпирических данных формируется математическая модель.

Математическая модель позволяет проводить различные эксперименты, что позволяет предсказывать возможные изменения при изменении начальных условий или параметров системы. Она также может служить для разработки новых стратегий управления или для оптимизации процессов.

Важно понимать, что математическая модель — это не самоцель, а инструмент для решения конкретных задач. Она помогает уточнить представление о системе, а также позволяет получить более точные результаты.

Какие принципы используются при создании математической модели?

При создании математической модели, необходимо учитывать ряд принципов, которые позволяют создать точную и функциональную модель.

Один из принципов заключается в том, чтобы собрать все доступные и необходимые данные для создания модели. Это могут быть данные о прошлых событиях, характеристики объекта, аналогичные исследования и т.д.

Важным принципом является установление целей и определение того, какая информация необходима для достижения этих целей. Таким образом, создание модели начинается с вопроса, какая информация необходима, а затем идет определение последовательности шагов для ее получения.

Еще одним принципом является учитывание принципа экономии: необходимо представить наиболее важные факторы, которые влияют на события или процессы в модели. Это позволяет создать более простую, но функциональную модель.

Кроме того, модель должна быть проверена и протестирована на корректность и точность, используя доступные данные и информацию. Принципы измерения и контроля являются важными при тестировании и оценке модели.

Все принципы выше являются основными для создания успешной математической модели. Их использование помогает получить точную и функциональную модель, которая может использоваться для прогнозирования и принятия решений при решении различных проблем.

Какие типы математических моделей существуют?

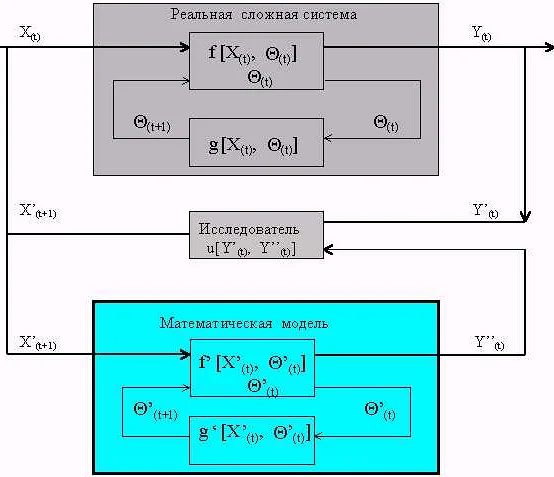
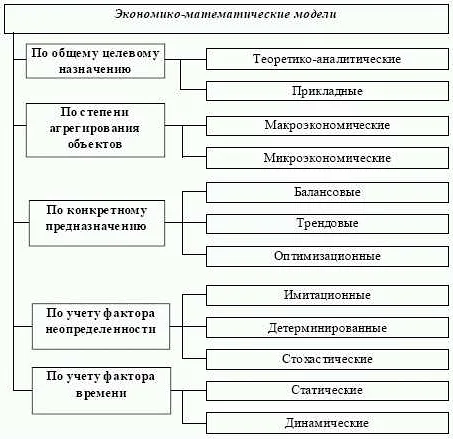
Математические модели могут быть созданы для описания различных явлений и процессов в разных областях науки и техники. Существует множество типов математических моделей, каждый из которых имеет свои преимущества и недостатки в зависимости от цели исследования, набора данных и условий задачи.

Некоторые из наиболее распространенных типов математических моделей:

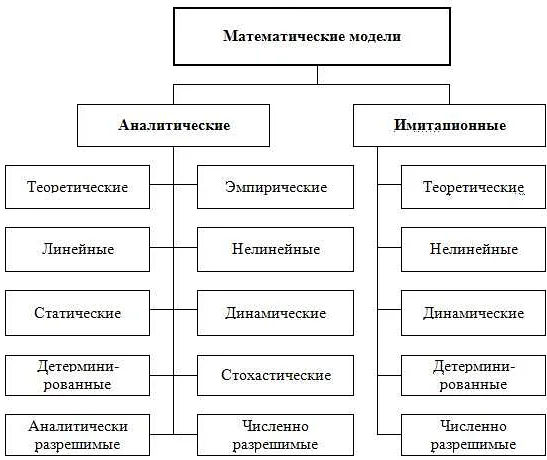
• Аналитические модели — модели, которые могут быть представлены математическими формулами или уравнениями. Они могут быть использованы для описания явлений, которые можно выразить аналитически, и обладают высокой степенью точности.
• Статистические модели — модели, которые основаны на анализе статистических данных и информации. Они могут быть использованы для прогнозирования свойств и поведения систем на основе наблюдаемых данных и статистических закономерностей.
• Компьютерные модели — модели, которые могут быть созданы с помощью компьютерных программ и алгоритмов. Они могут быть использованы для моделирования сложных систем и процессов, которые не могут быть описаны аналитически или статистически.
• Физические модели — модели, которые основаны на физических принципах и законах. Они могут быть использованы для создания физических прототипов систем и устройств, а также для исследования физических свойств материалов и сред.
• Системные модели — модели, которые описывают целые системы и их взаимодействия. Они включают различные компоненты и элементы системы, а также их взаимодействие и поведение в разных условиях.

Каждый тип математических моделей имеет свои преимущества и недостатки в зависимости от конкретной задачи и требований. Выбор типа модели должен быть основан на тщательном анализе данных и условий задачи, а также на определении цели исследования.

Пример №1: Математическая модель роста населения

Математическая модель роста населения — это модель, используемая для описания динамики изменения численности населения в определенной территории во времени. Такая модель позволяет предсказать изменения населения, а также понять факторы, влияющие на его рост.

Для создания такой модели можно использовать различные математические подходы, например, метод экспоненциального роста. Согласно этому методу, рост населения является экспоненциальным, то есть пропорциональным текущему уровню населения.

Модель может также учитывать и другие факторы, влияющие на рост населения, такие как рождаемость, смертность и миграция. В результате получается более точная модель, которая может быть использована для прогнозирования будущего состояния населения.

Важно отметить, что математическая модель роста населения может быть полезна в различных областях, включая демографию, экономику и геополитику. Она может помочь оценить социально-экономические последствия изменения численности населения, а также принять меры для устойчивого развития территории.

Пример №2: Математическая модель распространения заболевания

Создание математической модели распространения заболевания может потребовать учета различных факторов, таких как скорость передвижения инфицированных людей, вероятность заражения в определенных условиях, время инкубации болезни и т.д.

Одной из наиболее распространенных моделей является SIR-модель, которая делит население на три группы: подверженных инфекции (S — susceptible), инфицированных (I — infected) и выздоровевших (R — recovered). Количество людей в каждой группе изменяется во времени в зависимости от параметров модели и начальных условий. (например, скорости заражения, смертности и т.п.)

Другой пример — SEIR-модель, которая, в отличие от SIR, включает в себя группу E — exposed (зараженных, но ещё не являющихся инфицированными, находящихся в период инкубации болезни).

Пример параметров для модели SIRПараметрОписаниеПример значения

β	коэффициент контакта	0.3
γ	коэффициент заболевания	0.05
α	коэффициент выздоровления	0.01

Эти параметры могут быть использованы для создания упрощенных моделей, которые могут помочь в предсказании того, как быстро может распространиться заболевание и какие меры контроля могут быть наиболее эффективными.

Пример №3: Математическая модель банковской системы

Банковская система представляет собой сложную систему отношений между различными участниками, такими как люди, компании, правительство и др. Математическая модель банковской системы позволяет изучать эти отношения и предсказывать, как изменения в одной области могут повлиять на другие области.

Модель может включать параметры, такие как процентные ставки, кредитные лимиты, условия обслуживания и т.д. Они могут быть представлены в виде уравнений и формул, которые могут быть использованы для прогнозирования и анализа различных сценариев.

Одним из ключевых элементов модели является баланс банка. Он описывает отношение между активами и пассивами банка и показывает, насколько стабильна его финансовая позиция. В модели можно изучать, как изменения в балансе банка повлияют на его способность предоставлять кредиты и выполнять другие функции.

Также в модели можно учитывать поведение клиентов и их реакцию на изменения в условиях обслуживания, а также внешние факторы, например, экономическую ситуацию в стране.

Математическая модель банковской системы может быть использована для принятия решений, которые помогут банку оптимизировать свою деятельность и обеспечить максимальную эффективность.

Пример №4: Математическая модель теплообмена

Математическая модель теплообмена является важным инструментом для предсказания теплообмена между теплоносителями в различных технических устройствах. В основе модели лежит закон сохранения энергии и уравнение теплопередачи.

Для создания математической модели теплообмена необходимо определить геометрические размеры теплообменника, расположение теплоносителей и тепловые потоки. Затем необходимо использовать уравнения для описания теплообмена в каждом из теплоносителей.

Результатом создания математической модели теплообмена являются уравнения, описывающие теплообмен в каждой из областей, а также уравнение граничных условий, которое описывает условия передачи тепла между теплоносителями в точках контакта.

Математическая модель теплообмена может быть использована для оптимизации системы теплообмена, так как позволяет предсказать тепловые потоки и использование теплоносителей в системе.

Примерами систем теплообмена, для которых создаются математические модели, могут служить системы отопления, кондиционирования воздуха, системы охлаждения и промышленные технологические установки.

Пример №5: Математическая модель движения транспортных средств

Математическая модель движения транспортных средств используется для определения скорости, габаритов и других параметров транспортных средств в зависимости от условий дорожного движения.

Для создания такой модели необходимо учитывать множество факторов, таких как масса, тип транспортного средства, скорость движения, состояние дороги и многие другие. В процессе моделирования необходимо установить соответствующие математические зависимости для каждого из этих факторов.

Кроме того, в модели должны учитываться такие явления, как трение, аэродинамическое сопротивление и силы инерции. Все эти факторы влияют на движение транспортного средства и должны быть учтены при создании математической модели.

Такая модель может быть использована для оценки безопасности движения на дорогах, а также для оптимизации эксплуатации и проектировании дорог и транспортных средств.

Моделирование движения транспортных средств является сложной и многогранной задачей, которая требует глубоких знаний в области физики, математики и технических наук.

Пример №6: Математическая модель электрической цепи

Математическая модель электрической цепи позволяет предсказывать поведение электрической цепи в зависимости от заданных входных параметров и внешних условий. Модель может быть использована для решения проблем, связанных с проектированием электрических цепей и оптимизацией их работы.

Основой математической модели электрической цепи являются уравнения Кирхгофа, которые описывают законы сохранения энергии и заряда. В уравнениях Кирхгофа учитываются элементы цепи — проводники, резисторы, конденсаторы и индуктивности.

Для создания математической модели электрической цепи необходимо определить значения параметров цепи — сопротивления, емкости, индуктивности. Затем необходимо решить уравнения Кирхгофа и получить систему уравнений, описывающую поведение цепи во времени.

Математическая модель электрической цепи может быть реализована в виде программного кода, который позволяет моделировать работу цепи и изменять ее параметры. Такая модель может быть использована для оптимизации работы цепи, а также для создания новых электрических устройств.

Использование математической модели электрической цепи позволяет экономить время и ресурсы, необходимые для создания и оптимизации электрических цепей. Благодаря математической модели можно предсказать поведение цепи в различных условиях и выбрать наиболее оптимальные параметры для ее работы.

Пример №7: Математическая модель экономического цикла

Математическая модель экономического цикла — это математическая модель, которая описывает повторяемые колебания экономической активности во времени. Экономический цикл — это периодическое изменение конъюнктуры национальной экономики, которое характеризуется заметным изменением темпа роста производства и уровня занятости. Модель экономического цикла позволяет исследовать влияние различных экономических факторов на периоды бума и спада в экономике.

Математическая модель экономического цикла может быть представлена в виде системы дифференциальных уравнений, которые описывают изменение промышленного выпуска, инвестиций, занятости и других экономических показателей во времени. Для создания такой модели необходимо провести сбор и анализ данных о состоянии экономики, чтобы определить основные факторы, влияющие на экономический цикл.

Математическая модель экономического цикла может быть использована для прогнозирования экономических кризисов, а также для разработки эффективных мер по их предотвращению. Она может помочь правительству и бизнесу принимать обоснованные решения в сфере экономики, учитывая возможные последствия на будущее.

Создание математической модели экономического цикла требует глубокого понимания экономических закономерностей, а также высокой квалификации в области математики и статистики. Для успешного создания такой модели необходимо строго следовать этапам моделирования и использовать точные и достоверные данные.

Пример №8: Математическая модель генетического алгоритма

Генетический алгоритм – это метод оптимизации, вдохновленный принципами эволюционного процесса в природе. Он использует механизмы наследования, мутации и отбора, чтобы создавать новые решения на основе уже существующих.

Математическая модель генетического алгоритма состоит из нескольких компонентов: начальной популяции, функции пригодности, операторов отбора, кроссинговера и мутации.

1. Начальная популяция – это набор случайных решений, которые служат отправной точкой для оптимизации.
2. Функция пригодности – это мера качества каждого решения в популяции. Она определяет, насколько хорошо решение соответствует заданным требованиям.
3. Операторы отбора – это методы выбора родительских решений, которые будут использоваться для создания новых решений в следующем поколении.
4. Кроссинговер – это оператор, который комбинирует информацию от родительских решений для создания потомства.
5. Мутация – это оператор, который случайным образом изменяет некоторые компоненты решения.

Совмещение этих компонентов позволяет генетическому алгоритму находить оптимальные решения в задачах оптимизации. Он может быть использован для решения самых разнообразных задач, таких как поиск оптимальной конфигурации оборудования или настройка параметров алгоритма машинного обучения.

Математическая модель генетического алгоритма может быть реализована на языке программирования, таком как Python или Java, путем написания соответствующего кода для каждого из компонентов. Такой код позволяет автоматизировать процесс оптимизации и получать быстрые и точные результаты.

Пример №9: Математическая модель физического процесса

Математические модели не ограничиваются только техническими задачами, они также могут применяться в физических процессах. Рассмотрим пример, как можно создать математическую модель физического процесса.

Представим скорость свободного падения тела на Землю. На практике эта скорость составляет около 9,81 м/с². Мы можем создать математическую модель, которая описывает связь между высотой падения и скоростью тела.

Для этого необходимо использовать уравнение движения свободного падения:

h = v₀t + (gt²)/2

где:

• h — высота падения
• v₀ — начальная скорость, равная 0
• t — время падения
• g — ускорение свободного падения, равное 9,81 м/с²

Используя эту математическую модель, мы можем определить скорость тела на определенной высоте. Таким образом, математические модели могут быть очень полезными в физических процессах при расчете и предсказании траектории движения тела.

Вопрос-ответ:

Что такое математическая модель?

Математическая модель — это абстрактная система уравнений, которая описывает поведение реальной системы и используется для предсказания ее поведения в будущем. Модель может быть создана для любой области знаний, где можно выразить зависимости между переменными через математические выражения.

Как создать математическую модель?

Для создания математической модели сначала необходимо проанализировать объект, который будет моделироваться, и определить его ключевые свойства. Затем необходимо выбрать подходящую математическую формулу или систему уравнений, которая будет описывать эти свойства. Далее нужно определить значения параметров и начальных условий модели и провести расчеты для получения результата.

Какие примеры математических моделей вы можете привести?

Некоторые примеры математических моделей включают в себя модели изменения климата, модели экономической деятельности, модели движения жидкостей и газов, модели генетических систем и модели движения тел в пространстве.

Какие математические методы используются при создании моделей?

При создании математических моделей могут использоваться различные методы, включая дифференциальное и интегральное исчисление, статистические методы, линейную алгебру и численные методы решения уравнений. В зависимости от задачи и объекта моделирования выбирается соответствующий метод.

Как узнать, насколько точна математическая модель?

Для оценки точности математической модели используются различные методы, включая статистический анализ, сравнение с экспериментальными данными и валидация модели. Оценка точности модели является важным шагом, так как позволяет определить, насколько можно доверять результатам, полученным с помощью модели.

Какие преимущества имеют математические модели перед экспериментальными исследованиями?

Математические модели позволяют проводить исследования в условиях, которые трудно или невозможно воссоздать в реальном мире. Кроме того, они позволяют получить быстрый и относительно дешевый результат, не требуя больших затрат на оборудование и эксперименты. Также модели могут использоваться для предсказания поведения системы в будущем и для проведения оптимизации параметров.

Какие недостатки могут иметь математические модели?

Одним из основных недостатков математических моделей является их упрощенность и необходимость учета только самых важных переменных, что может привести к неточности и ограниченности моделей в реальном мире. Кроме того, математические модели требуют определенных знаний и навыков для их создания и анализа, что может ограничить их использование.

Пример №10: Математическая модель управления производством

Математическая модель управления производством является инструментом, который помогает оптимизировать рабочие процессы на производстве. Она учитывает различные параметры, такие как количество рабочих, скорость производства и загрузку оборудования. Модель позволяет определить оптимальный баланс ресурсов и максимальную эффективность производства.

Для создания модели необходимо собрать данные о всех процессах, которые происходят на производстве. Затем эти данные должны быть проанализированы, чтобы выявить закономерности и связи между различными факторами. Из этих данных создается математическая модель управления, которая может быть использована для прогнозирования производственных процессов и оптимизации режима работы.

Математическая модель управления производством может быть представлена в виде уравнения или системы уравнений, которые описывают все процессы, происходящие на производстве. Она может быть использована как для решения конкретных задач, так и для определения стратегии развития производства.

В основе модели лежит математическая теория, поэтому ее создание требует высокой квалификации и специализированных знаний. Однако, если модель создана правильно, она может значительно повысить эффективность работы производства и увеличить прибыль компании.

• Преимущества математической модели управления производством:
• Позволяет оптимизировать рабочие процессы и повысить эффективность производства;
• Позволяет определить оптимальный баланс ресурсов и максимальную загрузку оборудования;
• Позволяет прогнозировать производственные процессы и оптимизировать режим работы;
• Позволяет определить стратегию развития производства.

Таким образом, математическая модель управления производством является необходимым инструментом для компаний, которые хотят оптимизировать процессы на производстве. Создание модели требует высокой квалификации и специализированных знаний, но при правильном подходе она может значительно улучшить работу производства и повысить прибыль компании.

Видео по теме: