Интерпретация результата математической модели: что это такое и как её правильно понимать

Интерпретация результата математической модели – это процесс объяснения полученных данных и оценки их значимости. При этом учитываются как теоретические, так и практические аспекты, а также возможные ограничения и недостатки самой модели. Узнайте, как правильно интерпретировать результаты исследования математической модели и что может влиять на их точность и достоверность.

Математические модели являются неотъемлемой частью современной науки и техники. Они помогают предсказывать поведение объектов и систем, а также оптимизировать процессы различных видов. Среди наиболее часто используемых математических моделей можно выделить модели экономики, биологии, физики и техники.

Однако, как правило, результаты математических моделей непосредственно используют только специалисты в соответствующих областях знаний. Часто результаты, полученные при помощи математических методов, могут показаться довольно абстрактными и неочевидными для тех, кто не имеет соответствующего образования. Именно в этой ситуации на помощь приходит процедура интерпретации результатов математической модели.

Интерпретация результатов математической модели – это процесс объяснения значения и значения выводов, полученных с помощью математической модели. Этот процесс может включать объяснение того, какие параметры играют роль в модели, какие факторы оказывают наибольшее влияние на результаты, и так далее. Интерпретация результатов математической модели позволяет пользователям понимать, как применять полученные результаты в определенных ситуациях, и улучшить качество принимаемых ими решений.

Понимание математических моделей

Математическая модель – это описание процесса, явления или системы, привязанное к конкретным числам. Она используется для предсказания будущих событий, и для принятия решений.

Математическая модель может быть представлена в виде уравнений, графиков, таблиц или других математических символов. При этом, математическая модель может быть простой или сложной, в зависимости от того, насколько подробно описывается изучаемый процесс.

Чтобы понимать математическую модель, необходимо иметь хорошее математическое образование и уметь анализировать математические уравнения и символы. Также важно уметь интерпретировать результаты математической модели, чтобы применять их в практических задачах.

Понимание математических моделей имеет большое значение в научных областях, таких как физика, биология, химия, экономика и многих других. Также эта навык полезен в решении задач в производственных и коммерческих организациях.

Умение работать с математическими моделями помогает принимать обоснованные решения и определять возможные последствия действий. Поэтому, оно является одним из важнейших инструментов в процессе принятия решений.

Видео по теме:

Важность интерпретации результатов

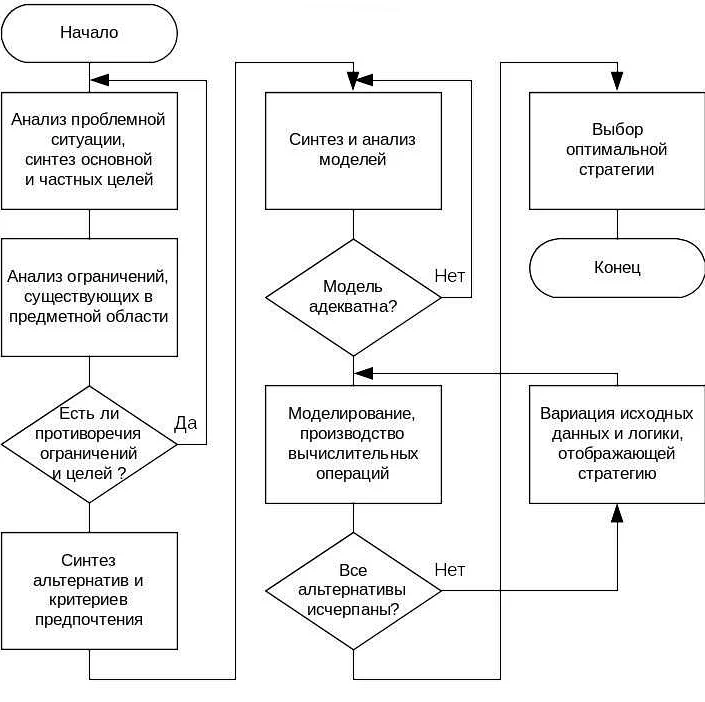
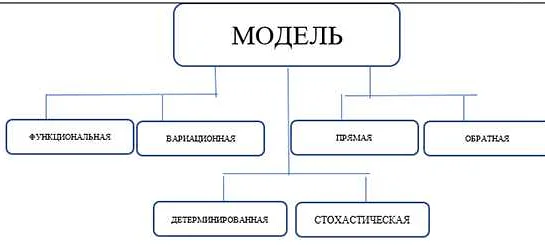
Математическая модель является мощным инструментом для решения различных задач в науке, технике, экономике и других областях. Однако, результаты моделирования не могут быть просто приняты как абсолютная истина, необходимо их критически оценивать и интерпретировать.

Интерпретация результатов моделирования позволяет понять, какие факторы оказывают наибольшее влияние на решение проблемы, какие могут быть допущены при применении модели, какие выводы можно сделать и какие ограничения есть у модели.

Кроме того, интерпретация результатов позволяет получить более точное и глубокое понимание процессов, которые моделируются, что может привести к улучшению модели и ее применения в будущем.

Таким образом, интерпретация результатов моделирования является важным шагом, который позволяет получить полную картину и сделать правильные выводы в конкретной ситуации.

Помощь в принятии решений

Математическая модель может помочь в принятии различных решений. Например, если мы моделируем производственный процесс, то можем использовать модель для прогнозирования времени выполнения задач и оценки затрат на производство. Это позволяет улучшить планирование и оптимизировать процессы, что приводит к экономии времени и денег.

Другой пример использования математической модели — в области финансов. Модель может помочь предсказать, как изменятся инвестиционные портфели в зависимости от различных факторов. Такие модели могут помочь инвесторам принимать более обоснованные решения, основываясь на данных и нескольких сценариях развития событий.

Еще один пример использования математической модели — в медицинском исследовании. Моделирование может помочь исследователям понять, как различные лекарства воздействуют на организм и какие побочные эффекты могут возникнуть. Это может помочь разработать более эффективные и безопасные лекарства для пациентов.

• Важно понимать ограничения модели. Всегда нужно помнить, что математическая модель — это упрощенное представление реальности. Модель может не учитывать все факторы, которые влияют на процесс или являются неизвестными на данный момент. Поэтому важно понимать, что любое принятое решение может не быть идеальным.
• Необходимо уметь интерпретировать результаты. Результаты модели могут быть сложными для понимания, поэтому важно уметь интерпретировать их. Например, если мы моделируем производственный процесс и получаем оценку затрат на производство, нужно понимать, какие факторы на нее влияют и какие изменения могут привести к снижению затрат.
• Следует разрабатывать несколько сценариев. В реальной жизни события могут развиваться по-разному, поэтому важно разработать несколько сценариев. Это поможет убедиться, что решение, основанное на модели, будет действительно эффективным в самых различных ситуациях.

Социальный контекст применения

Математические модели находят широкое применение в социальной сфере. Они используются для анализа социальных явлений, таких как распространение заболеваний, эпидемий и распространение информации в социальных сетях.

Также математические модели применяются для оптимизации ресурсов и повышения качества жизни в социальном контексте. Например, они могут быть использованы для оценки и управления рисками, которые связаны со строительством и реконструкцией городской инфраструктуры.

Моделирование, используемое в социальной сфере, помогает выявлять проблемы и искать оптимальные решения для улучшения жизни и благополучия людей.

Чтобы эффективно применять математические модели в социальном контексте, необходимо учитывать различные факторы, такие как экономические, политические и культурные особенности той или иной страны или региона. Важен также учет мнения, потребностей и интересов людей, которые затрагиваются моделированием.

Таким образом, социальный контекст применения математических моделей имеет огромную важность, так как он учитывает множество факторов, влияющих на социальные процессы и помогает найти наилучшие решения для улучшения качества жизни людей.

Предсказание результатов

Математические модели применяются для предсказания результатов в различных областях: от экономики до медицины. Они могут помочь оценить, как изменения входных данных повлияют на выходные параметры модели.

Прогнозирование результатов может быть особенно полезно для принятия решений в условиях неопределенности, когда нет возможности провести исследование в реальных условиях. Например, моделирование поведения рынка или воздействия лекарственных препаратов на организм человека.

Однако не следует забывать, что процесс предсказания результатов при помощи математической модели является лишь приближением и не может учесть все факторы, влияющие на реальный результат. Поэтому при принятии решений на основе таких моделей всегда необходимо учитывать возможную погрешность и являться осторожным.

Также стоит отметить, что модели нуждаются в обновлении и доработке, если новые данные приведут к изменению факторов, влияющих на результат. В противном случае, прогнозируемые результаты могут быть неточными или даже неверными.

В целом, предсказание результатов при помощи математических моделей является полезным инструментом для анализа и принятия решений в различных сферах, но необходимо помнить о возможной погрешности и не полагаться только на результаты моделирования.

Определение степени точности

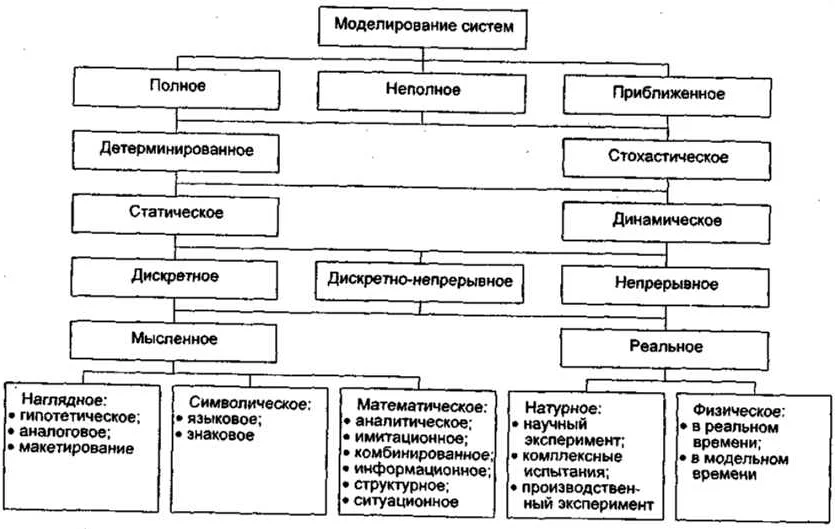
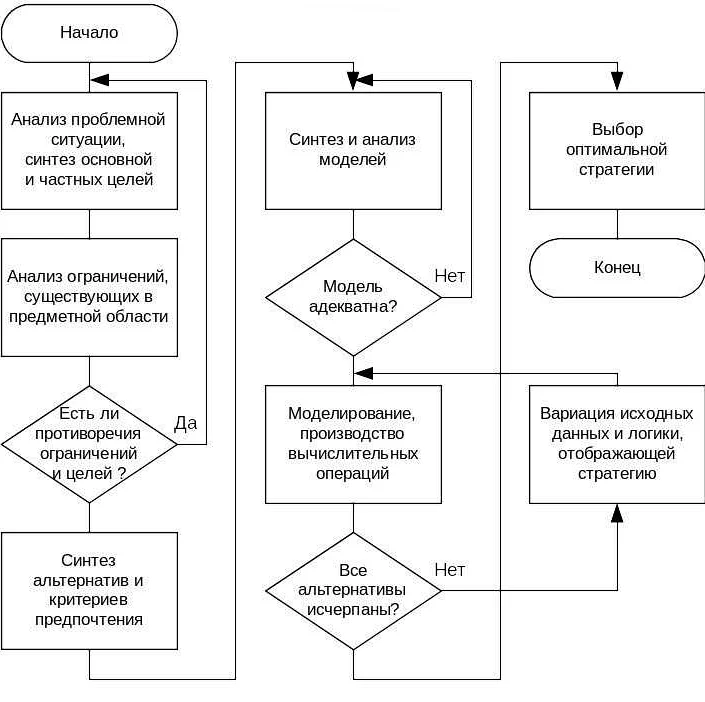
Для того, чтобы оценить качество результата моделирования, необходимо определить степень точности. Эта степень точности указывает, насколько близко значение, полученное в результате работы модели, к реальным данным.

Для определения степени точности можно использовать различные методы. Один из них — сравнение полученных результатов с результатами, полученными на основе реальных данных. Также можно проводить анализ ошибок, которые возникают при работе модели. Если их количество слишком велико, значит, рассчитанные значения неправильны, а модель нуждается в доработке.

Другой метод заключается в том, чтобы сравнить результаты, полученные при использовании разных моделей. В таком случае можно выбрать наиболее точную модель, для перспективных предсказаний.

В любом случае, определение степени точности модели — это необходимый этап при работе с математическими моделями. Только так можно выявить ее сильные и слабые стороны, а также дополнительные нюансы, которые можно учитывать в дальнейшей работе.

Сравнение с другими моделями

Когда речь идет о математических моделях, необходимо понимать, что они могут быть разными. Одна и та же система может быть описана различными способами, и каждый из них будет иметь свои достоинства и недостатки.

Сравнение моделей между собой позволяет выбрать ту, которая лучше всего подходит для конкретной задачи. Для этого необходимо оценить точность каждой модели, ее сложность и время, необходимое для ее создания.

Иногда возможно объединение нескольких моделей в одну, так называемую гибридную модель. Это позволяет устранить недостатки каждой отдельной модели и получить более точный результат.

Однако, важно помнить, что правильный выбор модели зависит от того, для какой задачи она используется. Например, линейная модель может быть более точной в одних условиях, а полиномиальная в других.

• Преимущества сравнения моделей:
  1. выбор наиболее точной модели;
  2. сохранение времени на разработку и использование нескольких моделей вместо одной;
  3. возможность объединения нескольких моделей в гибридную.
• Недостатки сравнения моделей:
  • необходимость проведения дополнительных экспериментов для выбора наиболее подходящей модели;
  • несколько более высокий уровень сложности и объем времени на проведение сравнения.

Различия в интерпретации результатов для разных моделей

Каждая математическая модель в своей интерпретации результата имеет свои особенности. Модели, использующие вероятностный подход, учитывают стохастические (случайные) факторы, что позволяет описать большое количество сценариев. Интерпретация результата такой модели основывается на вероятностных распределениях и их параметрах.

Детерминистические модели дают точные значения, которые не содержат случайных величин, и их интерпретация привязана к конкретным значениям входных параметров. Для таких моделей важно убедиться, что входные данные доступны и надежны.

Сетевые модели допускают использование разных методов решения, что может привести к различным результатам. Интерпретация таких результатов зависит от выбранного метода и его ограничений.

Многофакторные модели, использующие несколько параметров, могут помочь в понимании взаимосвязи различных факторов. Интерпретация результата такой модели может потребовать статистического анализа и проверки значимости параметров.

Таким образом, выбор модели и ее интерпретация зависит от цели исследования и ее предметной области. Особенности каждой модели необходимо учитывать при интерпретации результата.

Влияние на исследовательскую деятельность

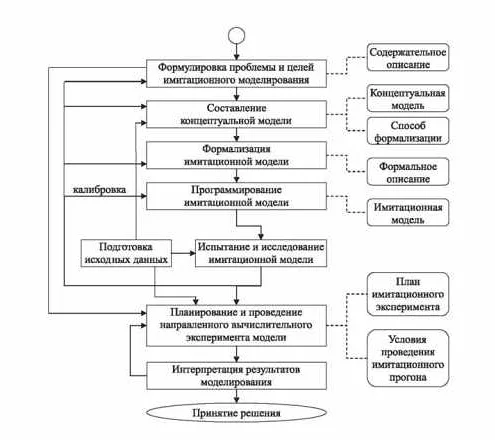
Математические модели играют важную роль в научных исследованиях. Они позволяют предсказывать поведение системы, проводить эксперименты в виртуальном пространстве и выделять наиболее значимые факторы. Интерпретация результатов математической модели позволяет принимать взвешенные решения и корректировать стратегию исследования.

В контексте исследовательской деятельности интерпретация результатов математической модели может повлиять на ряд аспектов:

• выбор методов исследования;
• сбор данных и определение их значимости;
• оценка вероятности получения желаемого результата;
• принятие решения об изменении области, в которой исследуется система;
• разработка дальнейшей стратегии эксперимента.

Интерпретация результатов математической модели позволяет минимизировать риски и предотвращать нежелательные последствия. Более того, она может расширить горизонты исследования, помочь в создании новых уникальных методов, и, в результате, привести к новым открытиям и инновациям.

Примеры интерпретации результатов

Пример 1

Математическая модель была построена для анализа влияния температуры и влажности на рост растений. Результаты модели показали, что при определенном сочетании температуры и влажности рост растений ускоряется, и что влажность оказывает более существенное влияние, чем температура. Это означает, что при определенных условиях рост растений можно ускорить, контролируя влажность.

Пример 2

Математическая модель использовалась для предсказания возможного роста цен на нефть в ближайшие годы. Результаты модели показали, что цены на нефть будут продолжать расти в ближайшие годы, но снизятся после 2025 года. Это может быть связано с увеличением добычи сланцевой и скважинной нефти, а также с развитием альтернативных источников энергии. Предсказание результатов модели поможет инвесторам и экономистам сделать более обоснованные решения в отношении инвестирования в нефтяную промышленность.

Пример 3

Математическая модель была использована для анализа рисков заболевания COVID-19 в разных частях мира. Результаты модели показали, что риск заболевания зависит от многих факторов, включая густонаселенность, степень соблюдения мер безопасности, медицинскую помощь и т.д. Интерпретация результатов модели поможет правительствам и общественным организациям принимать более эффективные меры по борьбе с пандемией.

• Математическая модель может быть использована для анализа разных видов данных и является одним из важнейших инструментов современной науки.
• Интерпретация результатов модели помогает делать обоснованные выводы и принимать взвешенные решения в разных отраслях деятельности, в том числе в экономике, медицине, геологии, космических исследованиях и т.д.
• Результаты математических моделей могут быть представлены в разных форматах, включая диаграммы, таблицы и графики.

Вопрос-ответ:

Зачем нужна интерпретация результата математической модели?

Интерпретация результата математической модели позволяет понять, какие выводы можно сделать на основе полученных данных, и как этот результат можно использовать в реальной жизни. Она помогает оценить взаимосвязь между переменными в модели и выявить влияние каждой из них на итоговый результат.

Как происходит интерпретация результата математической модели?

Интерпретация результата математической модели происходит путем анализа полученных данных и определения их значимости. Часто используются статистические методы для проверки гипотез, выбора оптимальных параметров и проверки точности модели. Интерпретация может включать в себя графическую визуализацию результатов и объяснение их с помощью теории и практики в соответствующей области знаний.

Какие цели могут быть достигнуты с помощью интерпретации результата математической модели?

Интерпретация результата математической модели может помочь в принятии эффективных решений, улучшении процессов и оптимизации производственных циклов. Она может использоваться для прогнозирования будущих событий, выявления проблем в работе системы и их устранения. Также интерпретация может помочь в сравнении различных моделей и выборе наилучшей.

Какие области знаний используют математические модели и их интерпретацию?

Математические модели и их интерпретацию используют в различных областях знаний, таких как экономика, финансы, бизнес, медицина, наука и технология. Они могут использоваться для прогнозирования рынка, определения оптимальных цен на товары, анализа затрат и прибыли компании, выявления тенденций в медицинских данных, создания новых научных теорий и многое другое.

Какова роль математической модели в интерпретации?

Математическая модель представляет собой упрощенную, но формализованную версию реальной системы или процесса. Она используется для установления взаимосвязей между переменными и определения их влияния на результат. Интерпретация результата математической модели позволяет понять, какие выводы можно сделать на основе полученных данных, и как этот результат можно использовать в реальной жизни. Разработка и интерпретация математической модели обычно требует большого количества данных, аналитических и статистических методов и экспертных знаний в соответствующей области знаний.

Как определить точность математической модели в интерпретации ее результата?

Точность математической модели в интерпретации ее результата можно определить путем сравнения предсказанных значений с реальными данными. Для этого используются различные статистические показатели, такие как коэффициент детерминации, корреляция, средняя квадратичная ошибка и другие. Если модель хорошо соответствует реальной системе и имеет высокие показатели точности, то можно считать, что ее результаты могут быть использованы для принятия эффективных решений.

Могут ли результаты интерпретации математической модели быть неверными?

Да, результаты интерпретации математической модели могут быть неверными, если модель содержит ошибки или неточности в данных, если используются неправильные методы интерпретации или если она не соответствует реальной системе. Поэтому важно проводить тщательный анализ данных и проверять точность модели перед ее использованием для принятия решений. Также необходимо учитывать, что математическая модель не может учесть все варианты развития событий и она дает только приблизительное представление о реальной системе.