Кто придумал ноль в математике

Узнайте, кто и когда придумал ноль в математике и как это важное понятие повлияло на развитие науки и технологий. Исследуйте историю нуля и его значение в современной математике.

Нуль — это число, которое обозначает отсутствие чего-либо или пустоту. В современной математике нуль считается одним из основных чисел, но его понятие не всегда было столь очевидным. Интересно, что этот символ, как и само понятие нуля в математике, возникли не так уж и давно.

Одним из первых упоминаний о нуле можно считать индийский математический трактат «Варга-куламба» I века н.э., где упоминается пустое пространство в контексте вычислений. Однако именно в Индии, в V веке н.э., нуль приобрел свою символическую запись: кружок, который с течением времени стал похож на цифру «0».

Знак «0» был введен в западную математику в VI веке арабскими математиками. Они позаимствовали его у индийцев и начали активно использовать в своих вычислениях. Восточные и арабские математики, такие как Аль-Хорезми и Аль-Хазени, считали нуль числом и использовали его в алгебре и арифметике. Благодаря арабским ученым, нуль распространился по всей Европе и стал неотъемлемой частью математических вычислений.

Однако понимание нуля как числа требовало определенных усовершенствований в математической теории. Вплоть до XVII века ученые сталкивались с различными противоречиями, связанными с операциями, содержащими ноль. Большой вклад в исследование нуля внесли математики Рене Декарт, Джордано Бруно, Георг Кантор и другие. Именно их работы и привели к формализации понятия нуля и его применению в различных областях математики и науки.

История возникновения нуля в математике

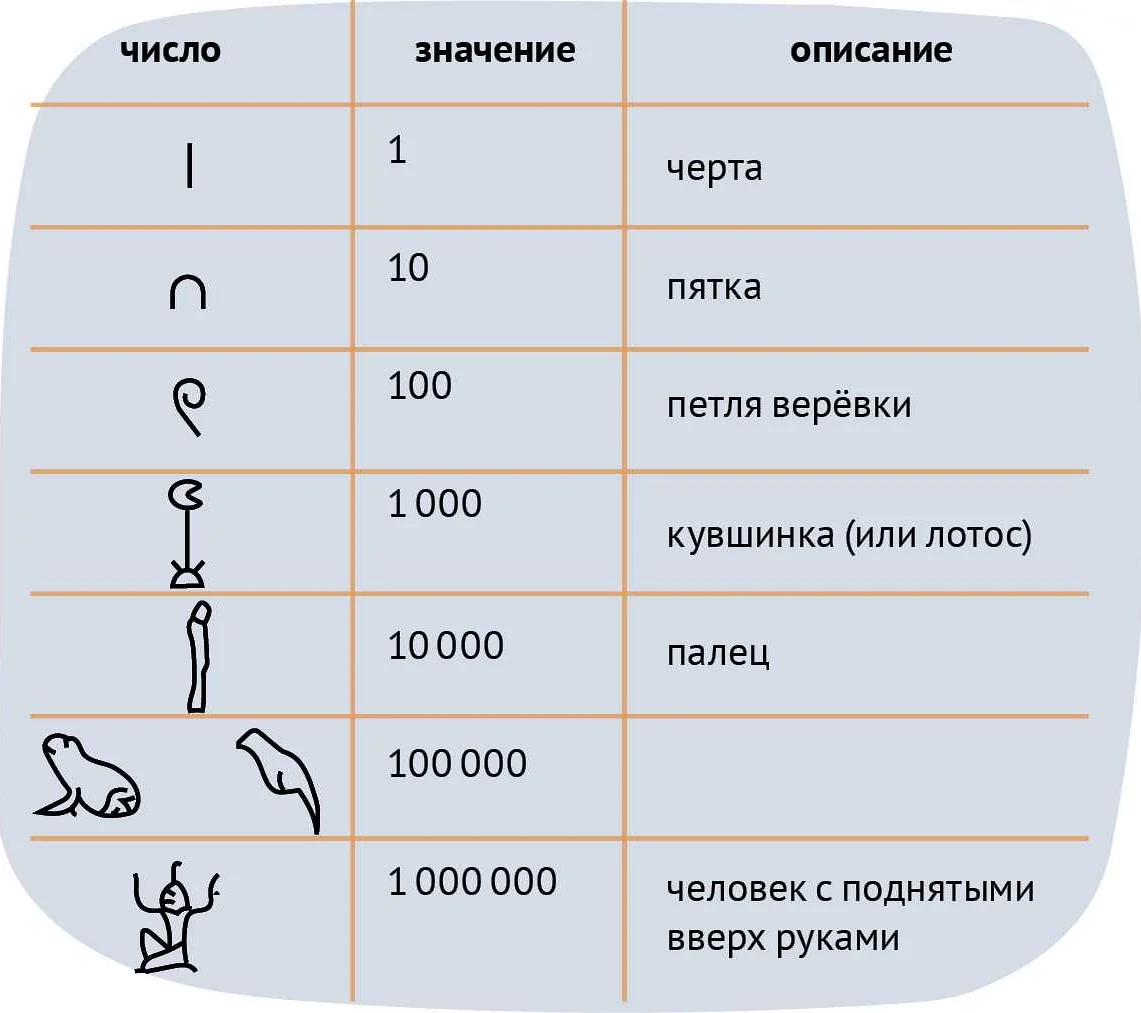
Первоначально, древние цивилизации не использовали понятие нуля в своих вычислениях. Например, древние египтяне использовали систему счисления, основанную на десятичной системе, но не имели символа, который представлял бы ноль.

Появление нуля в математике связывают с развитием десятичной системы счисления в древней Индии. В V веке н.э. арабские математики познакомились с индийскими математическими работами, в которых использовался символ для обозначения нуля. Арабы внесли значительный вклад в развитие математики и распространили знание о нуле в западный мир.

Однако, нуль как математическое понятие не был принят сразу. В западной математике нуль был непростым числом, и его использование было ограничено. Вплоть до XVIII века нуль оставался спорным числом и вызывал много дебатов среди математиков.

Использование нуля как числа существенно изменило математику и наше понимание чисел. Благодаря нулю возможно представление чисел в позиционной системе счисления, что облегчило арифметические операции и деление на ноль.

В итоге, нуль стал неотъемлемой частью математики, и его значения и свойства широко изучаются в современной науке.

Видео по теме:

Поиски начала числовой системы

Первые упоминания о нуле встречаются в индийских математических текстах, написанных около V века н.э. В этих текстах ноль обозначался с помощью горизонтальной черты или круга. Однако настоящий символ нуля — точка, появился только в VII веке н.э. в Индии.

Символ нуля был впервые использован как цифра в индийской десятичной системе счисления, известной как систе

Древние цивилизации и отсутствие нуля

В древних цивилизациях, таких как древний Египет и Месопотамия, отсутствие нуля было распространено. Эти цивилизации использовали различные системы счета, но ни одна из них не включала нуля в качестве отдельного числа.

В древнем Египте использовалась система счета на основе десяти. Они использовали глиняные таблички, называемые абаками, для счета. Однако древние египтяне не использовали специальный символ для обозначения нуля.

Подобная ситуация была и в Месопотамии, где использовалась система счисления на основе шести. Они также использовали абаки для счета, но не имели символа нуля.

Отсутствие нуля в этих древних системах счета создавало определенные ограничения. Например, невозможно было точно выразить ноль или отсутствие чего-либо в этих системах. Это существенно затрудняло некоторые математические вычисления.

Появление нуля в математике было революцией, которая произошла позже, в индийской математике. Индийские математики разработали систему счисления, которая включала нуль в качестве отдельного числа, а также использовали его как позиционный цифровой символ. Именно из этой индийской системы счисления нуль распространился по всему миру и стал неотъемлемой частью нашего понимания чисел.

Индийская математика и открытие нуля

Первые упоминания о нуле как математическом понятии встречаются в древнеиндийском тексте «Лилавати» из XII века н.э., написанном математиком Бхаскарой. Однако, следы нуля можно найти и в более ранних индийских текстах, таких как «Суриясидханта» и «Брахма-сфута-сиддханта».

Индийские математики использовали знак «шунья», что означало «пустоту» или «пустую колбу». Этот знак был использован для обозначения нуля как числа и как позиции в числе, что сделало возможным развитие позиционной системы счисления.

Открытие нуля имело огромное значение для математики. Оно позволило сделать более точные вычисления, разработать новые методы и алгоритмы. Введение нуля также позволило решать уравнения и считать числа больше 9, что привело к развитию алгебры и теории чисел.

Индийская математика и открытие нуля имели огромное влияние на развитие математики в других регионах мира. Знание о нуле распространилось через Арабский мир в Европу и в конечном итоге стало основой для развития современной математики.

Таким образом, благодаря индийской математике и открытию нуля мы получили новое понимание чисел и возможность проводить более сложные вычисления, что существенно изменило наше представление о мире и его математической структуре.

Путешествие нуля в Аравию

Начало истории

Ноль – это одно из самых фундаментальных понятий в математике. Он играет роль базового элемента в нашей системе счисления, позволяя создавать числа разных величин и значений. Но откуда взялся этот знак, обозначающий «ничто» или «отсутствие»? История возникновения нуля уходит своими корнями в древний Восток, а именно в Аравию.

Адвайта, основоположник нуля

В V веке нашей эры в Аравии появился математик Адвайта. Он внес значительный вклад в развитие различных наук, включая алгебру и геометрию. Однако, его самым важным вкладом стало введение символа «0», который он использовал для обозначения пустоты или отсутствия значения. Благодаря его труду к числам была добавлена еще одна важная составляющая – ноль.

Распространение нуля

Идея нуля быстро распространилась по всей Аравии и впоследствии добралась до Индии. Там она была значительно развита и стала основой для создания десятичной системы счисления. Именно эта система сейчас используется по всему миру и является стандартной в большинстве стран.

Нуль в Европе

Несмотря на важность этого числа, в Европе его использование было долго запрещено. Некоторые ученые считали, что ноль – это идея, противоречащая естеству чисел, и отвергали его в своих трудах. Однако, в XIII веке идея нуля проникла в Европу через арабских ученых, и вскоре стала всеобщепризнанным символом.

Значимость числа ноль

С появлением нуля числа стали более универсальными и гибкими. Ноль позволил нам оперировать большими и очень маленькими числами, а также ввести отрицательные числа. Без нуля наша математика была бы сильно ограничена, и многие ее важные концепции не смогли бы развиться.

Итоги

Таким образом, путешествие нуля началось в Аравии, где Адвайта ввел его в математику. Затем идея распространилась по всему Востоку и добралась до Европы. Сегодня ноль играет важную роль в нашей системе счисления, позволяя нам оперировать числами и проводить сложные математические вычисления.

Нуль в современной математике

Нуль используется в арифметических операциях, таких как сложение, вычитание, умножение и деление. Он является источником для формирования других чисел с помощью различных операций. Например, умножение любого числа на ноль дает результат ноль.

Нуль также играет важную роль в алгебре и анализе. Например, в алгебре нуль является нейтральным элементом относительно сложения: любое число плюс ноль равно этому числу. В анализе нуль активно используется при определении границ функций и решении уравнений.

Один из интересных фактов о нуле заключается в том, что он является единственным числом, которое не относится ни к положительным, ни к отрицательным числам. Он занимает особое место на числовой прямой и играет важную роль в математических моделях и теориях.

В современной математике нуль имеет широкий спектр применений и является неотъемлемой частью нашего понимания чисел и их взаимодействия. Он является фундаментальным концептом, который помогает решать различные проблемы и задачи в науке, технике и других областях знания.

Роль нуля в алгебре и геометрии

Нуль играет важную роль в алгебре и геометрии, дополняя и расширяя наше понимание чисел и их отношений.

В алгебре, ноль является нейтральным элементом в сложении и вычитании. Как только мы добавляем ноль к любому числу, его значение не меняется. Ноль также является нейтральным элементом в умножении на ноль. Умножение на ноль всегда дает ноль, независимо от другого множителя.

В геометрии, ноль играет роль начала координатной системы. В двумерной координатной плоскости, ноль находится в центре, где пересекаются оси x и y. В трехмерной координатной системе, ноль находится в точке, где пересекаются оси x, y и z.

Ноль также играет важную роль в матрицах и системах уравнений. В матрицах, ноль может быть использован для создания нулевых или нулевых строк и столбцов, что помогает в решении систем уравнений и выполнении матричных операций.

Роль нуля в алгебре и геометрии не может быть преувеличена. Он предоставляет нам базовые понятия и инструменты для работы с числами и объектами в математике, что помогает в развитии более сложных концепций и решении разнообразных задач.

Нуль и его значение в современном мире

В математике ноль является нейтральным элементом относительно сложения и вычитания. Это означает, что при сложении нуля с любым числом, результат будет равен этому числу. А при вычитании нуля из любого числа, результат также будет равен этому числу. Это свойство нуля делает его неотъемлемой частью математических операций и вычислений.

Ноль играет важную роль в физике и науке. Он используется для измерения относительной позиции и изменений величин. Например, температура, измеряемая в градусах Цельсия или Фаренгейта, имеет ноль в качестве точки отсчета. Ноль также используется для обозначения отсутствия заряда, например, в электрических цепях.

В информатике и компьютерных науках ноль играет важную роль в битовых операциях и в представлении чисел. Он используется для обозначения отсутствия значения или информации. Ноль также является основным элементом в двоичной системе счисления, которая является основой для работы компьютеров и цифровых устройств.

Кроме того, ноль имеет философский и символический смысл. Он часто ассоциируется с пустотой, отсутствием или началом. Ноль может символизировать возможность нового начала или чистого листа. В различных культурах и религиях ноль имеет свои особенности и некоторые дополнительные значения.

Таким образом, нуль является важным числом, которое имеет широкое применение в математике, физике, науке, информатике и даже культуре. Его значение в современном мире нельзя недооценивать, поскольку оно является одним из основных строительных блоков нашего развитого общества.

Вопрос-ответ:

Какой смысл имеет ноль в математике?

Ноль в математике обозначает отсутствие чего-либо или нулевую величину. Это также является началом числовой шкалы и играет важную роль в различных математических операциях.

Кто изобрел ноль и когда это произошло?

Изобретение нуля в математике приписывается разным культурам, но наиболее известным считается его появление в древней Индии примерно в 5 веке н.э. Оттуда он распространился в другие части мира через арабских ученых.

Как ноль изменил наше понимание чисел?

Введение нуля в математику позволило создать позиционную систему счисления, которая является основой современной математики. Без нуля было бы невозможно выполнять арифметические операции, записывать и работать с большими числами.

Как ноль используется в различных областях математики?

Ноль используется в различных областях математики. В алгебре он является нейтральным элементом для сложения и вычитания. В геометрии ноль служит центром координатной системы. В теории вероятностей он используется для описания событий, которые не могут произойти. И это только некоторые примеры.

Что произойдет, если исключить ноль из математики?

Если исключить ноль из математики, то наша математическая система стала бы неполной и некоторые операции, такие как деление на ноль, стали бы неопределенными. Кроме того, многие математические модели и уравнения потеряли бы свою точность и применимость.

Кто придумал ноль?

Ноль был придуман древнеиндийскими математиками в V веке. В то время он изображался символом пустого пространства и использовался в качестве позиционного числа. Однако, его полноценное введение в математику произошло только в IX веке благодаря работам арабских ученых.

Как ноль изменил наше понимание чисел?

Введение нуля в математику изменило наше понимание чисел, ведь это стало основой для развития алгебры и позиционной системы счисления. Ноль позволил нам различать неполные и полные числа, а также использовать их в операциях с числами. Благодаря нулю, мы можем записывать числа любой величины и выполнять сложные математические операции.