Перечислите признаки по которым классифицируются математические модели

В данной статье мы рассмотрим основные признаки, по которым классифицируются математические модели, включая их тип, структуру, способ представления и область применения. Узнайте, как определить и выбрать подходящую модель для конкретной задачи.

Математические модели являются важным инструментом во многих областях науки и техники. Они позволяют представить сложные процессы и явления в виде формальных математических конструкций, которые можно анализировать и использовать для прогнозирования и оптимизации.

Существует несколько способов классифицировать математические модели в зависимости от их свойств и характеристик. Одним из основных признаков, по которому можно классифицировать модели, является тип функциональной зависимости. Некоторые модели используют простые аналитические формулы, например, линейные или экспоненциальные функции. Другие модели основаны на дифференциальных уравнениях, интегральных уравнениях или разностных уравнениях.

Еще одним важным признаком классификации моделей является степень детализации. Некоторые модели представляют общую картину процесса, учитывая только основные факторы и закономерности. Другие модели учитывают большее количество взаимосвязей и деталей, что позволяет более точно описывать реальные явления и проводить более сложные и точные расчеты.

Также модели можно классифицировать по степени стохастичности. Стохастические модели учитывают случайные факторы и шум, которые могут влиять на результаты моделирования. Детерминированные модели, напротив, представляют собой точные математические выражения без учета случайных воздействий.

Другие признаки классификации моделей включают в себя типы переменных, которые есть в модели (например, дискретные или непрерывные переменные), возможность учитывать неопределенность и нечеткость данных, а также способы оценки и верификации моделей.

Применение различных классификаций позволяет более точно описывать и анализировать различные виды математических моделей, а также выбирать наиболее подходящие методы и подходы для решения конкретных задач.

Классификация математических моделей: основные признаки

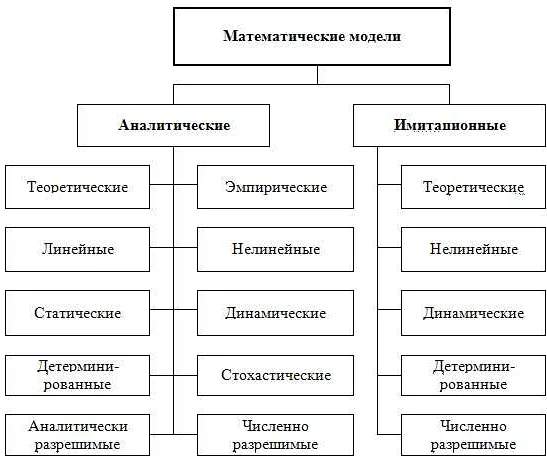
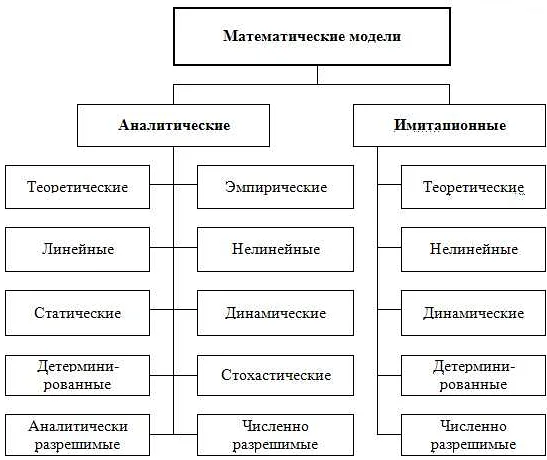
1. Явность. Математическая модель может быть явной, если она представлена в виде аналитической формулы, либо неявной, если ее уравнения задаются в виде отношений или условий, которые должны быть выполнены.
2. Дискретность или непрерывность. Математическая модель может быть дискретной, если она описывает систему, в которой изменения происходят в дискретные моменты времени или пространства. В случае непрерывной модели изменения происходят непрерывно во времени или пространстве.
3. Линейность или нелинейность. Математическая модель может быть линейной, если ее уравнения являются линейными по отношению к неизвестным переменным и их производным. В противном случае модель считается нелинейной.
4. Статическая или динамическая. Математическая модель может быть статической, если она описывает систему в единичный момент времени. Динамическая модель описывает изменение системы со временем.
5. Детерминированная или стохастическая. Математическая модель может быть детерминированной, если ее поведение можно предсказать с абсолютной точностью. Стохастическая модель учитывает случайность или неопределенность в поведении системы.
6. Однородная или неоднородная. Математическая модель может быть однородной, если она описывает систему, в которой параметры и условия не изменяются со временем или пространством. Если параметры и условия меняются, модель считается неоднородной.

Понимание основных признаков классификации математических моделей позволяет исследователям выбрать подходящий метод и адекватно описать и анализировать систему, которую они изучают. Каждый признак классификации имеет свои особенности и применяется в разных областях науки и техники.

Видео по теме:

Степень абстракции в моделировании

Высокая степень абстракции предполагает упрощение модели и игнорирование некоторых деталей или особенностей исследуемой системы. Такие модели часто используются при исследовании сложных систем, когда точное описание всех взаимосвязей и параметров затруднительно или невозможно.

Низкая степень абстракции, наоборот, подразумевает максимально детальное описание системы, включая все ее компоненты, взаимодействия и особенности. Такие модели используются в случаях, когда требуется точное предсказание поведения системы и учет всех факторов, влияющих на ее функционирование.

Степень абстракции в моделировании может быть представлена в виде шкалы, где на одном конце находится абстрактная модель, а на другом – детальная. Конкретная степень абстракции выбирается в зависимости от целей и задач исследования.

Таким образом, степень абстракции является важным аспектом в выборе и использовании математических моделей. Она позволяет находить компромисс между уровнем детализации модели и ее практической применимостью.

Преимущества высокой степени абстракцииПреимущества низкой степени абстракции

Упрощение моделирования	Точное предсказание поведения системы
Сокращение времени и затрат на исследование	Учет всех факторов, влияющих на функционирование системы
Понимание общих закономерностей и свойств системы	Выявление скрытых зависимостей и взаимосвязей

Вид математических функций в моделях

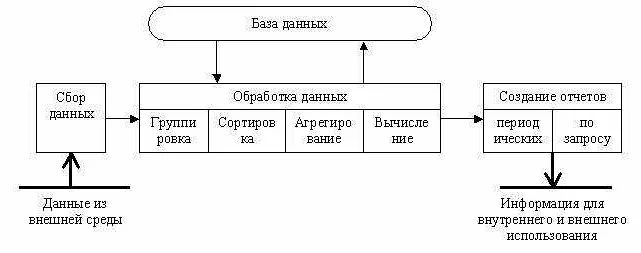
Математические модели используют различные виды математических функций для описания и предсказания различных явлений и процессов. В зависимости от типа задачи и требуемой точности модели, выбираются соответствующие функции.

Одной из наиболее распространенных функций, используемых в математических моделях, является линейная функция. Она представляет собой прямую линию на графике, где значение зависимой переменной меняется пропорционально значению независимой переменной. Линейные функции широко применяются в экономических и финансовых моделях, а также в задачах оптимизации.

Еще одной распространенной функцией является показательная функция. Она имеет вид y = a^x, где a — постоянное число, а x — независимая переменная. Показательные функции широко используются в моделях роста популяций, распространения инфекций и в других задачах, где требуется учитывать экспоненциальный рост.

Также в математических моделях часто применяются логарифмические функции. Они используются для описания процессов, где изменение величины зависит не от самой величины, а от ее логарифма. Логарифмические функции часто используются в физических моделях, а также в задачах статистики и экономики.

Помимо этих основных типов функций, в математических моделях могут применяться и другие виды функций, такие как степенная функция, гиперболическая функция, тригонометрические функции и др. Выбор функции зависит от конкретной задачи и требований к модели.

Вопрос-ответ:

Какие основные признаки классификации математических моделей существуют?

Основные признаки классификации математических моделей включают: тип модели (аналитическая, графическая, имитационная), характер взаимодействия переменных (детерминированная, стохастическая), степень детализации модели (макро-, мезо-, микромодель), степень формализации модели (формальная, полуформальная, неформальная), степень приближения модели к реальности (идеализированная, реалистическая), а также цель моделирования (описательная, предсказательная, оптимизационная).

Чем отличается аналитическая модель от графической и имитационной?

Аналитическая модель представляется в виде математических уравнений, формул и алгоритмов. Графическая модель представляет собой графическую диаграмму или схему, использующую различные символы и стрелки для обозначения взаимосвязей между переменными. Имитационная модель основана на использовании компьютерных программ, которые моделируют поведение системы на основе имитации ее реального функционирования.

Что такое детерминированная и стохастическая модели?

Детерминированная модель предполагает, что значения переменных в модели являются точными и предсказуемыми, без каких-либо случайных факторов. Стохастическая модель учитывает случайные факторы и неопределенность, представляя значения переменных в виде вероятностных распределений.

Какие бывают степени детализации моделей?

Степень детализации модели может быть макро-, мезо- или микромоделью. Макромодель представляет общую картину системы, учитывая ее основные характеристики и взаимосвязи без детального учета малых изменений. Мезомодель учитывает большее количество деталей и более конкретные характеристики системы. Микромодель учитывает все детали системы и каждую ее составляющую в отдельности.

Какие бывают степени приближения моделей?

Степень приближения модели может быть идеализированной или реалистической. Идеализированная модель упрощает реальную систему, игнорируя некоторые детали и сложности, чтобы упростить анализ. Реалистическая модель более точно отражает реальность, учитывая все важные факторы и характеристики системы.

Линейные и нелинейные математические модели

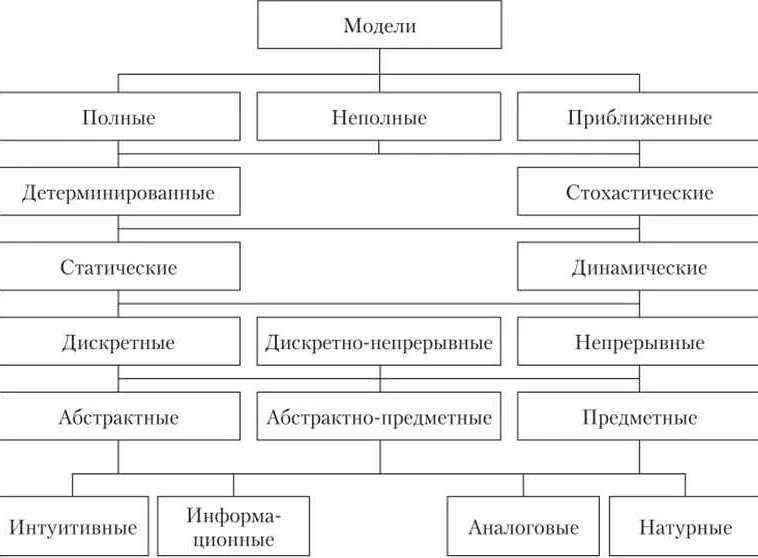
Особенность линейных моделей заключается в том, что изменение величины одной переменной пропорционально изменению другой переменной. Это означает, что график линейной модели представляет собой прямую линию.

Например, уравнение y = mx + b, где y и x — переменные, m — коэффициент наклона, b — точка пересечения с осью y, является линейной моделью. Здесь изменение переменной x на единицу приведет к изменению переменной y на m единиц.

Нелинейные модели, в отличие от линейных, описывают нелинейные связи между переменными. В таких моделях изменение одной переменной может приводить к нелинейным изменениям другой переменной.

График нелинейной модели может иметь различные формы, такие как парабола, гипербола, экспоненциальная кривая и др.

Примером нелинейной модели является уравнение y = a * x^2 + b * x + c, где y и x — переменные, а, b и c — коэффициенты. В этом уравнении изменение переменной x может влиять на переменную y нелинейным образом.

Линейные и нелинейные модели используются в различных областях, включая физику, экономику, биологию и другие. Выбор между линейной и нелинейной моделью зависит от природы изучаемой системы и целей исследования.

Линейные моделиНелинейные модели

Простота интерпретации	Большая гибкость
Предсказуемость	Способность моделировать сложные явления
Легкость в решении	Точность в описании реальности

Дискретные и непрерывные модели

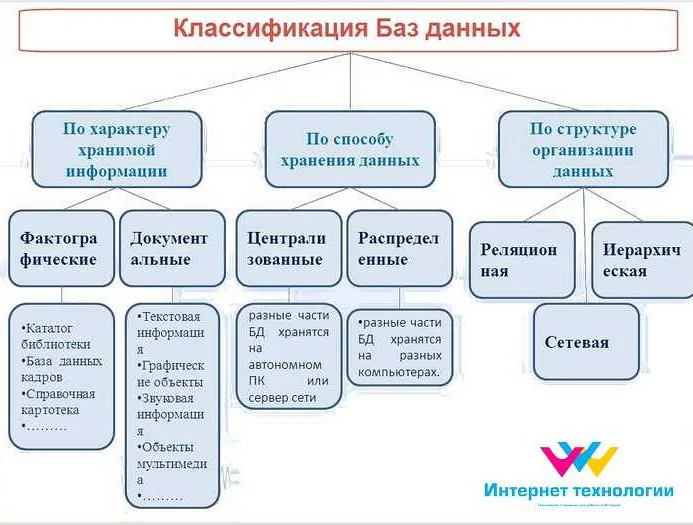
Дискретные модели описывают системы, в которых переменные изменяются только в определенные моменты времени или значения производятся только на конечных наборах точек. Такие модели представляются в виде дискретных последовательностей или таблиц. Например, в задачах теории вероятностей используются дискретные модели для описания случайных величин, которые принимают только определенные значения.

Непрерывные модели, напротив, описывают системы, в которых переменные могут принимать любые значения в определенном интервале. Такие модели представляются в виде функций, графиков или уравнений. Например, в задачах физики или экономики используются непрерывные модели для описания изменения физических величин или экономических показателей в непрерывном времени.

Выбор между дискретными и непрерывными моделями зависит от конкретного контекста и требований задачи. Некоторые системы естественно описываются дискретными моделями, в то время как другие лучше поддаются непрерывному описанию. Важно учесть этот признак при выборе и применении математической модели для решения конкретных задач.

Статические и динамические модели

Статическая модель — это модель, которая не учитывает изменений во времени. Она описывает состояние системы в определенный момент времени, независимо от того, как она пришла к этому состоянию или что произойдет после этого. В статической модели система рассматривается как статичная и неизменная.

Динамическая модель, наоборот, учитывает изменения во времени. Она описывает, как система меняется со временем и какие факторы влияют на эти изменения. Динамическая модель может предсказывать будущие состояния системы на основе текущих условий и входных данных.

Обычно динамические модели используются для изучения процессов и явлений во времени, таких как движение, рост, изменение популяции и другие. Статические модели, с другой стороны, используются для анализа состояний системы в определенный момент времени, например, для описания статистических данных или статического равновесия.

Обе категории моделей имеют свои преимущества и недостатки, и выбор между ними зависит от конкретной задачи и целей исследования. Важно понимать, что статические и динамические модели не являются взаимоисключающими и могут быть комбинированы для более полного и точного описания системы.

Однозначные и многозначные модели

Математические модели могут быть разделены на две основные категории: однозначные и многозначные. Разница между ними заключается в том, какие значения принимают переменные в модели.

Однозначные модели предполагают, что каждому значению независимой переменной соответствует одно и только одно значение зависимой переменной. Это означает, что при заданных значениях независимой переменной всегда можно однозначно определить значение зависимой переменной. Примером однозначной модели может служить простая линейная функция y = kx + b, где k и b — постоянные коэффициенты.

Многозначные модели, наоборот, предполагают, что независимой переменной могут соответствовать различные значения зависимой переменной. Значения зависимой переменной могут быть неоднозначными и зависеть от других факторов или условий. Примером многозначной модели может служить квадратичная функция y = ax^2 + bx + c, где a, b и c — коэффициенты, которые могут принимать различные значения.

Однозначные модели используются там, где требуется точное предсказание и установление причинно-следственной связи между переменными. Многозначные модели предпочтительны, когда требуется учесть неопределенность и возможность нескольких вариантов развития событий.

Экспертные и статистические модели

Математические модели могут быть разделены на две основные категории: экспертные и статистические модели. Обе эти категории имеют свои особенности и применяются в различных областях.

Экспертные модели создаются на основе знаний и опыта экспертов в конкретной области. Они используют субъективные оценки и мнения экспертов для предсказания и описания явлений. Экспертные модели часто применяются, когда отсутствует достаточное количество данных или когда данные не могут быть собраны и проанализированы.

Статистические модели, в свою очередь, основаны на статистических методах и анализе данных. Они используют объективные данные для построения моделей и прогнозирования. Статистические модели широко применяются для анализа данных, выявления зависимостей и предсказания будущих событий.

Каждая из этих категорий имеет свои преимущества и ограничения. Экспертные модели позволяют учитывать субъективные факторы и экспертное мнение, что может быть важно в некоторых областях, где данные ограничены или неполные. Статистические модели, в свою очередь, обладают большей объективностью и могут быть применены в случаях, когда имеется достаточное количество данных.

Важно отметить, что выбор между экспертными и статистическими моделями зависит от конкретной задачи и доступных ресурсов. В некоторых случаях может быть целесообразно комбинировать оба подхода для достижения наилучших результатов.

Вероятностные и детерминистические модели

Математические модели могут быть классифицированы на вероятностные и детерминистические. Вероятностные модели основаны на теории вероятностей и используют случайные величины для описания неопределенности в данных. Детерминистические модели, напротив, не учитывают случайности и представляют собой точные математические формулы или уравнения.

Вероятностные модели позволяют моделировать системы, в которых величины и события могут иметь случайное или вероятностное поведение. Они находят широкое применение в статистике, экономике, физике и других науках. Вероятностные модели могут быть использованы для прогнозирования, классификации и принятия решений в условиях неопределенности.

Примерами вероятностных моделей являются стохастические дифференциальные уравнения, марковские цепи, байесовские сети и многое другое. Вероятностные модели часто используются для моделирования случайных процессов, таких как финансовые рынки, погода, эпидемии и пр.

Детерминистические модели представляют собой математические уравнения или формулы, которые описывают систему точно и однозначно, без учета случайности. Они основаны на точных измерениях, начальных условиях и заранее известных параметрах. Детерминистические модели позволяют предсказать поведение системы в будущем на основе текущего состояния системы.

Примерами детерминистических моделей являются дифференциальные уравнения, линейные и нелинейные алгебраические уравнения, системы линейных уравнений и другие. Детерминистические модели широко применяются в физике, инженерии, экономике и других областях для анализа и оптимизации систем.

Важно отметить, что в реальном мире многие модели могут содержать как элементы вероятностных, так и детерминистических моделей. Например, в экономике можно использовать детерминистическую модель для описания поведения цен на рынке, но при этом учитывать случайные факторы, такие как изменение спроса или предложения.