Математическая модель которая описывает поведение и свойства

Математическая модель — это абстрактная математическая структура, которая описывает поведение и свойства реальных объектов или явлений. Она позволяет представить сложные системы в виде уравнений и формул, которые можно анализировать и использовать для прогнозирования будущих событий. В этой статье мы рассмотрим основные принципы создания математических моделей и их применение в различных областях знания.

Математическая модель – это абстрактное представление реального явления или системы с помощью математических символов и уравнений. Она позволяет упростить сложные процессы и предсказать поведение объекта, основываясь на заложенных в модель законах и принципах. Математические модели используются во многих областях науки и техники, таких как физика, экономика, биология и т.д.

Основные принципы построения математической модели включают выбор входных и выходных переменных, формулировку уравнений, описывающих связи между этими переменными, а также определение начальных и граничных условий. Важным шагом является проверка модели на соответствие экспериментальным данным и ее корректировка при необходимости.

Примером математической модели может служить модель распространения инфекции, основанная на уравнениях, описывающих динамику заболеваемости и выздоровления. С помощью такой модели можно предсказать, как быстро распространится инфекция в определенной популяции и какие меры необходимо принять для ее контроля.

Математические модели играют важную роль в науке и практике, позволяя предсказывать и оптимизировать различные процессы и явления. Они помогают лучше понять сложные системы и принимать обоснованные решения на основе научных данных. В дальнейшем развитие математических моделей может привести к созданию новых технологий и открытию новых закономерностей в природе и обществе.

Математические модели поведения и свойств: основные принципы и примеры

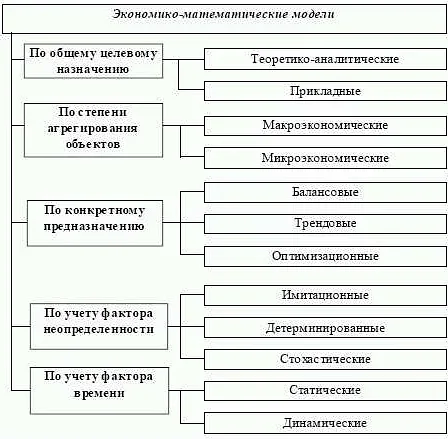
Математические модели играют важную роль в науке и инженерии, позволяя описывать и предсказывать поведение и свойства различных систем. Они основаны на математических уравнениях, которые описывают взаимодействие между различными переменными и параметрами.

Основной принцип математических моделей заключается в том, что реальная система или явление представляются в виде математических уравнений. Эти уравнения могут быть дифференциальными, алгебраическими или комбинацией обоих видов. Они описывают зависимости между различными переменными и параметрами, которые характеризуют систему.

Примером математической модели может служить модель распространения эпидемии. В данном случае переменными могут быть количество зараженных, количество людей, подверженных заражению, и время. Параметрами могут быть скорость заражения и временные характеристики болезни. Математическая модель в данном случае позволяет предсказывать динамику распространения эпидемии и оценивать эффективность различных мер по ее контролю.

Другим примером математической модели может служить модель движения тела под действием силы тяжести. В данном случае переменными могут быть положение, скорость и ускорение тела, а параметром будет масса тела. Математическая модель в данном случае позволяет предсказывать траекторию движения тела и оценивать его скорость и ускорение в различных точках.

Таким образом, математические модели позволяют описывать и анализировать различные системы и явления. Они могут быть использованы для прогнозирования поведения системы, оптимизации процессов и принятия решений. Использование математических моделей является важным инструментом в научных и инженерных исследованиях, а также в практическом применении в различных областях.

Видео по теме:

Определение математической модели

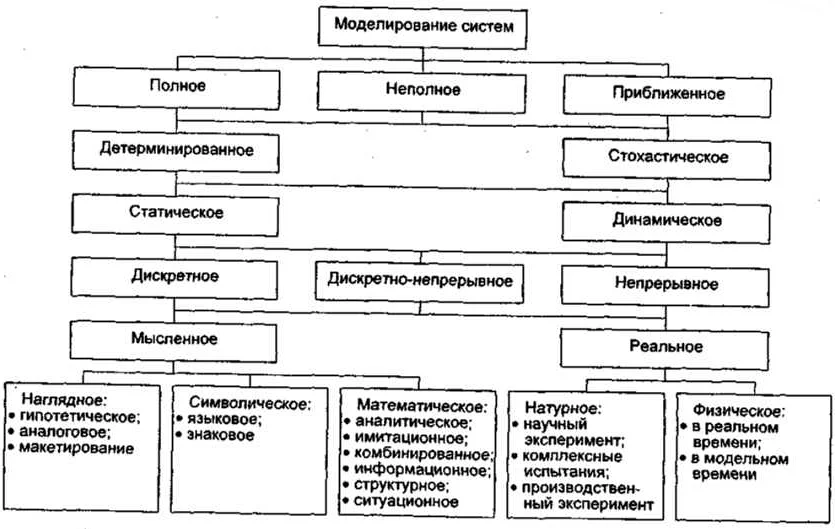
Математическая модель может быть представлена в виде графической схемы, системы уравнений, дифференциальных уравнений, статистических распределений и других математических конструкций.

Основная цель создания математической модели заключается в возможности анализа и прогнозирования поведения объекта или системы, а также в определении ее свойств.

Математическая модель может быть использована для решения различных проблем и задач, таких как оптимизация процессов, прогнозирование, управление системой, исследование и тестирование гипотез, анализ данных и т.д.

Для построения математической модели необходимо провести анализ объекта и его свойств, выделить основные факторы и отношения, определить математические законы и моделировать их с помощью математических операций.

Математическая модель является одним из ключевых инструментов в науке, технике, экономике и других областях знания, позволяющих исследовать и понимать сложные процессы и явления.

Примеры математических моделей

Модель роста популяции

Модель движения тела под действием силы

Модель распределения вероятностей

Модель экономического цикла

Важность математических моделей в науке и технике

Одной из важных задач математических моделей является предсказание результатов экспериментов и испытаний. С их помощью можно провести виртуальные эксперименты, что позволяет сэкономить время и ресурсы при проведении физических экспериментов.

Математические модели также позволяют проводить анализ и оптимизацию различных систем и процессов. С их помощью можно найти оптимальные параметры и условия, что позволяет улучшить эффективность и качество различных технических устройств и процессов.

Кроме того, математические модели играют важную роль в прогнозировании будущих событий и явлений. Они позволяют предсказывать развитие различных процессов и тенденций, что является важной информацией для принятия решений и планирования действий.

В итоге, математические модели являются незаменимым инструментом в науке и технике. Они позволяют исследовать сложные системы, предсказывать результаты и оптимизировать процессы. Благодаря математическим моделям мы можем лучше понять и контролировать окружающий мир и создавать новые технологии и устройства.

Вопрос-ответ:

Какие основные принципы лежат в основе математической модели поведения и свойств?

Основные принципы математической модели поведения и свойств включают в себя формализацию, анализ, прогнозирование и оптимизацию.

Что такое формализация в математической модели поведения и свойств?

Формализация представляет собой процесс описания системы с помощью математических символов, операций и функций.

Каким образом математическая модель поведения и свойств помогает в анализе системы?

Математическая модель позволяет провести анализ системы, выявить и описать взаимосвязи между различными переменными и параметрами, а также определить зависимости и закономерности поведения системы.

Можете привести примеры математических моделей поведения и свойств?

Конечно! Примерами математических моделей могут быть модель распространения эпидемии, модель роста популяции, модель экономического развития, модель движения тела под действием силы тяжести и другие.

Принципы построения математических моделей

Адекватность модели. Этот принцип предполагает, что модель должна отражать основные свойства и взаимодействия реальной системы, чтобы быть достоверной. Модель должна быть способна описывать наблюдаемые данные и предсказывать результаты эксперимента или события в реальной системе.

Простота модели. Модель должна быть как можно более простой и понятной, чтобы быть легко интерпретируемой и анализируемой. Слишком сложные модели могут быть трудными в использовании и требовать большого объема вычислительных ресурсов, а также могут вводить дополнительные неопределенности и ошибки.

Универсальность модели. Модель должна быть применима к различным ситуациям и условиям, чтобы быть универсальной. Чем больше ситуаций и условий модель способна описывать и предсказывать, тем более полезной она будет.

Проверяемость модели. Модель должна быть проверяемой и верифицируемой на основе экспериментальных данных или наблюдений в реальной системе. Проверка модели позволяет убедиться в ее достоверности и точности, а также корректировать и развивать модель при необходимости.

Адаптация модели. Модель должна быть гибкой и способной к адаптации при изменении условий или параметров. Реальные системы могут меняться со временем, и модель должна быть способна учитывать эти изменения и предсказывать их последствия.

Соблюдение данных принципов позволяет создавать надежные и эффективные математические модели, которые могут использоваться для анализа, прогнозирования и оптимизации различных систем и явлений.

Примеры математических моделей в физике

1. Модель движения тела под действием силы тяжести. Для описания этого движения используется уравнение свободного падения, которое можно записать в виде y = y0 + v0t — (1/2)gt^2, где y — вертикальная координата тела, y0 — начальная вертикальная координата, v0 — начальная вертикальная скорость, t — время, g — ускорение свободного падения.
2. Модель движения тела по окружности. Для описания этого движения используется уравнение окружности, которое можно записать в виде x = r*cos(ωt), y = r*sin(ωt), где x и y — координаты тела, r — радиус окружности, ω — угловая скорость, t — время.
3. Модель гармонического осциллятора. Для описания движения гармонического осциллятора используется уравнение гармонического осциллятора, которое можно записать в виде x = A*cos(ωt + φ), где x — координата осциллятора, A — амплитуда колебаний, ω — угловая скорость, t — время, φ — начальная фаза.
4. Модель распространения звука. Для описания распространения звука используются уравнения звуковых волн, которые связывают давление, плотность среды и скорость звука. Например, для одномерного случая можно использовать уравнение д’Аламбера: ∂^2p/∂t^2 = c^2 ∂^2p/∂x^2, где p — давление, t — время, x — координата, c — скорость звука.
5. Модель распространения света. Для описания распространения света используются уравнения электромагнитной волны, которые связывают электрическое и магнитное поля. Например, для плоской монохроматической волны можно использовать уравнение Гельмгольца: ∇^2E + k^2E = 0, где E — электрическое поле, k — волновой вектор.

Это лишь некоторые примеры математических моделей, используемых в физике. Они позволяют исследовать и предсказывать различные физические явления, а также создавать новые технологии и устройства на основе этих моделей.

Примеры математических моделей в экономике

Математическое моделирование активно применяется в экономике для исследования различных процессов и явлений. Ниже приведены некоторые примеры математических моделей, используемых в экономической науке:

1. Модель спроса и предложения

Эта модель основана на законах рынка и позволяет оценить взаимодействие спроса и предложения в определенной экономической ситуации. Она учитывает такие факторы, как цена, количество товара и предпочтения потребителей, а также затраты производителя на производство товара и его предложение на рынке.

2. Модель оптимального потребления

Эта модель помогает определить оптимальное потребление для индивида или группы индивидов с учетом их предпочтений и ограничений. Она учитывает такие факторы, как доход, цены на товары и услуги, предпочтения потребителей и ограничения в виде бюджетных ограничений.

3. Модель экономического роста

Эта модель используется для изучения экономического роста и развития. Она учитывает такие факторы, как инвестиции, производство, технологический прогресс и население. Модель помогает оценить влияние этих факторов на экономический рост и предсказать его долгосрочные тенденции.

4. Модель финансовых рынков

Эта модель используется для анализа финансовых рынков и прогнозирования их изменений. Она учитывает такие факторы, как цены акций, процентные ставки, объемы торгов и спрос на финансовые инструменты. Модель позволяет оценить риски и доходность инвестиций на финансовых рынках.

Это лишь некоторые примеры математических моделей, применяемых в экономике. Математическое моделирование позволяет более точно изучать и прогнозировать экономические процессы, делать более обоснованные решения и оптимизировать экономические системы.

Примеры математических моделей в биологии

Математические модели играют важную роль в изучении биологических процессов. Они позволяют описывать, объяснять и предсказывать различные явления, связанные с живыми организмами. Вот несколько примеров таких моделей:

1. Модель роста популяции

Эта модель используется для изучения динамики изменения численности популяции во времени. Она учитывает такие факторы, как рождаемость, смертность, миграция и другие влияющие на численность популяции факторы. Модель может быть представлена в виде дифференциального уравнения, которое описывает изменение численности популяции относительно времени.

2. Модель распространения инфекционных заболеваний

Эта модель используется для изучения динамики распространения инфекционных заболеваний в популяции. Она учитывает такие факторы, как передача инфекции, иммунитет, вакцинация и другие факторы, влияющие на распространение заболевания. Модель может быть представлена в виде системы дифференциальных уравнений, описывающих изменение численности инфицированных и восприимчивых к инфекции людей во времени.

3. Модель эволюции

Эта модель используется для изучения процессов эволюции организмов. Она учитывает такие факторы, как мутации, естественный отбор, генетический дрейф и другие факторы, влияющие на изменение генетического состава популяции во времени. Модель может быть представлена в виде системы дифференциальных уравнений или стохастических уравнений, описывающих изменение частот генов в популяции относительно времени.

Это лишь некоторые из примеров математических моделей, применяемых в биологии. Использование таких моделей позволяет более глубоко понять основные принципы и закономерности биологических процессов и предсказывать их поведение в различных условиях.

Примеры математических моделей в социологии

Математические модели активно используются в социологии для изучения различных социальных процессов и явлений. Они позволяют упростить сложные социальные системы и предсказывать их поведение на основе различных параметров.

Один из примеров математической модели в социологии – модель распространения информации в социальных сетях. Эта модель основана на идее, что люди влияют друг на друга и передают информацию через свои социальные связи. Модель учитывает такие факторы, как степень влияния каждого человека, время, необходимое для передачи информации, и вероятность передачи информации между связанными людьми. С помощью этой модели можно предсказать, как быстро и в каком объеме будет распространяться информация в социальной сети.

Еще один пример математической модели в социологии – модель формирования группового поведения. Эта модель используется для изучения того, как люди принимают решения в группе и какие факторы влияют на их поведение. Модель учитывает такие параметры, как личные предпочтения, социальное влияние и конфликты интересов. С помощью этой модели можно предсказать, какие решения будет принимать группа людей в определенной ситуации.

Также существуют математические модели, которые изучают динамику социальных сетей, эволюцию социальных структур и многие другие социальные явления. Эти модели помогают социологам лучше понимать и объяснять сложные социальные процессы и предсказывать их результаты. Они также позволяют проводить различные эксперименты и тестировать гипотезы в виртуальных условиях, что в некоторых случаях гораздо эффективнее и экономичнее, чем проводить такие исследования в реальной жизни.

Таким образом, математические модели в социологии играют важную роль в изучении и анализе социальных процессов и явлений. Они помогают упростить сложные социальные системы и предсказывать их поведение, а также проводить эксперименты и тестировать гипотезы в виртуальных условиях. Это позволяет социологам получать новые знания и лучше понимать социальный мир, в котором мы живем.