Физика и математика как найти диаметр

Как найти диаметр объекта с помощью физических и математических методов. Узнайте, как применить формулы и измерения для определения диаметра и получите точные результаты.

Диаметр — это одна из основных характеристик объектов в физике и математике. Он определяется как расстояние между двумя точками, находящимися на противоположных сторонах объекта и проходящими через его центр. Знание диаметра позволяет получить много информации о геометрических и физических свойствах объекта.

Найти диаметр можно по разным формулам, в зависимости от вида объекта и известных данных. В математике диаметр является одной из основных характеристик окружности, и для его вычисления используется простая формула: диаметр равен удвоенному радиусу. То есть, если известен радиус окружности, его можно умножить на 2, чтобы получить диаметр.

В физике диаметр используется для определения размеров различных объектов. Например, для определения диаметра планеты используется метод измерения угла, под которым видно планету с разных точек Земли. Зная расстояние между этими точками и используя тригонометрию, можно вычислить диаметр планеты. Также, диаметр используется для определения размеров шаров, цилиндров и других геометрических фигур.

Зная диаметр объекта, можно рассчитать его площадь или объем, а также предсказать его физические свойства и поведение в определенных условиях.

В данной статье мы рассмотрим несколько простых шагов, которые помогут вам найти диаметр объекта в физике и математике, а также приведем основные формулы, которые используются для этого расчета.

Что такое диаметр?

В математике диаметр широко используется для измерения размеров геометрических фигур, таких как окружности, сферы и прямоугольники. Для окружности диаметр является наибольшим отрезком, соединяющим две точки на ее краю и проходящим через ее центр. Диаметр окружности обычно обозначается буквой «d».

В физике диаметр используется для определения размеров различных объектов и систем. Например, диаметр атома используется для описания его размера, а диаметр планеты — для измерения ее физических характеристик, таких как объем и масса.

Диаметр также является важным параметром в механике и инженерии. Например, диаметр вала используется для определения его прочности и способности передавать механическую энергию. Диаметр трубы или кабеля определяет их пропускную способность и возможность передачи жидкостей или электрического тока.

Итак, диаметр — это важный параметр, используемый в физике и математике для измерения размеров и описания различных объектов и систем. Он позволяет точно определить расстояние между двумя точками на краях фигуры и описать ее важные характеристики.

Определение понятия диаметр в физике и математике

В физике диаметр может относиться к различным объектам и системам. Например, в случае сферы диаметр является расстоянием между двумя точками на ее поверхности, которые находятся на противоположных сторонах сферы. В случае цилиндра диаметр определяется как расстояние между двумя параллельными и равными друг другу окружностями, образующими его боковую поверхность. Аналогично, в случае конуса диаметр – это расстояние между двумя точками на его основании, которые находятся на противоположных сторонах.

В математике диаметр также широко используется для определения размерности и свойств геометрических фигур. Например, диаметр окружности является ее наибольшей прямой линией, которая делит окружность на две равные части. В общем случае, диаметр любой фигуры или объекта определяется как двукратное расстояние от центра до любой точки на его поверхности.

Знание и понимание понятия диаметра в физике и математике является важным для решения различных задач, а также для более глубокого изучения пространственных объектов и их характеристик.

Значение диаметра в различных областях науки

В физике и математике диаметр играет важную роль и имеет различное значение в разных областях науки:

1. Геометрия: В геометрии диаметр является прямой линией, проходящей через центр окружности и соединяющей две ее точки на противоположных сторонах окружности. Диаметр также является удвоенным значением радиуса.
2. Механика: В механике диаметр может использоваться для измерения размеров объектов, таких как трубы, шесты или шары. Диаметр шара используется для расчета объема и площади поверхности шарового объекта.
3. Электроника: В электронике диаметр может использоваться для определения размеров проводов, трубок или других электронных компонентов. Например, диаметр провода может быть важным параметром при определении его сопротивления.
4. Астрономия: В астрономии диаметр может использоваться для измерения размеров планет, звезд и других небесных объектов. Например, диаметр Земли составляет около 12 742 километров, а диаметр Солнца — около 1 391 000 километров.

Таким образом, диаметр имеет различное значение в разных областях науки и является важным параметром для измерений и расчетов.

Как найти диаметр в физике?

Существует несколько способов определить диаметр в физике, в зависимости от объекта и условий:

1. Измерение с помощью линейки или штангенциркуля. Для этого необходимо разместить объект на плоской поверхности и измерить расстояние между двумя противоположными точками на его поверхности. Полученное значение будет являться диаметром объекта.
2. Измерение с помощью микроскопа или другого оптического прибора. Если объект слишком маленький, чтобы быть измеренным с помощью линейки, можно использовать микроскоп или другой оптический прибор. Необходимо разместить объект под прибором и измерить расстояние между двумя крайними точками его изображения. Это расстояние будет являться диаметром объекта.
3. Измерение с помощью эксперимента или вычисления. В некоторых случаях диаметр может быть определен с помощью эксперимента или вычисления. Например, для определения диаметра пузырька мы можем измерить его объем и применить соответствующую формулу для нахождения диаметра.

Важно учитывать единицы измерения при определении диаметра. В физике диаметр обычно измеряется в метрах (м) или их производных, но в некоторых случаях может использоваться и другие единицы измерения, такие как сантиметры (см) или дюймы (in).

Точное определение диаметра в физике может иметь большое значение для дальнейших исследований и расчетов. Поэтому необходимо использовать точные методы измерения и учитывать все факторы, которые могут влиять на результаты измерений.

Формула для вычисления диаметра в физических задачах

В физике существует несколько формул, позволяющих вычислить диаметр в различных ситуациях. Одна из наиболее широко используемых формул — это:

Д = 2R

где Д — диаметр, а R — радиус окружности или сферы.

Эта формула основана на связи между радиусом и диаметром, которая всегда составляет величину вдвое большую. Таким образом, чтобы найти диаметр, необходимо умножить радиус на 2.

Например, если у нас есть задача, в которой дан радиус сферы R = 5 см, то для вычисления диаметра нужно использовать формулу:

Д = 2 * 5 = 10 см

Таким образом, диаметр сферы составляет 10 см.

Формула для вычисления диаметра проста и может быть использована в различных физических задачах, где требуется знание размеров окружностей и сфер.

Примеры расчетов диаметра в физике

Пример 1:

Пусть у нас есть шар с известным объемом V. Чтобы определить его диаметр, можно использовать формулу:

d = 2 * (V / (4/3 * π))^(1/3)

Где d — диаметр, V — объем, а π (пи) — математическая константа, приближенное значение которой равно 3.14159.

Пример 2:

Рассмотрим пример с определением диаметра круга. Круг можно описать вокруг точки с радиусом r. Диаметр круга равен удвоенному радиусу:

d = 2 * r

Где d — диаметр, а r — радиус.

Пример 3:

Пусть у нас есть прямоугольная плоскость со сторонами a и b. Если на плоскости нарисован круг, то его диаметр можно найти с помощью следующей формулы:

d = √(a^2 + b^2)

Где d — диаметр, a и b — стороны прямоугольника.

Как найти диаметр в математике?

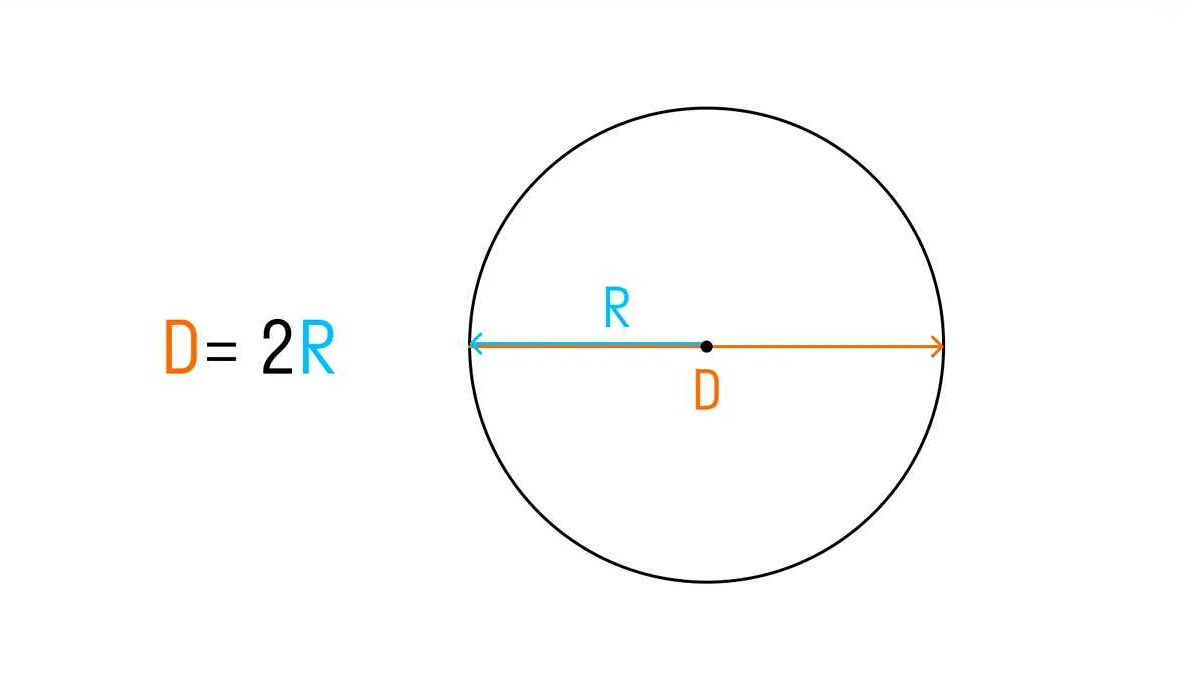
Для нахождения диаметра окружности необходимо знать ее радиус или длину окружности. Диаметр равен удвоенному радиусу окружности:

ФормулаОписание

Д = 2r

Диаметр окружности равен удвоенному радиусу

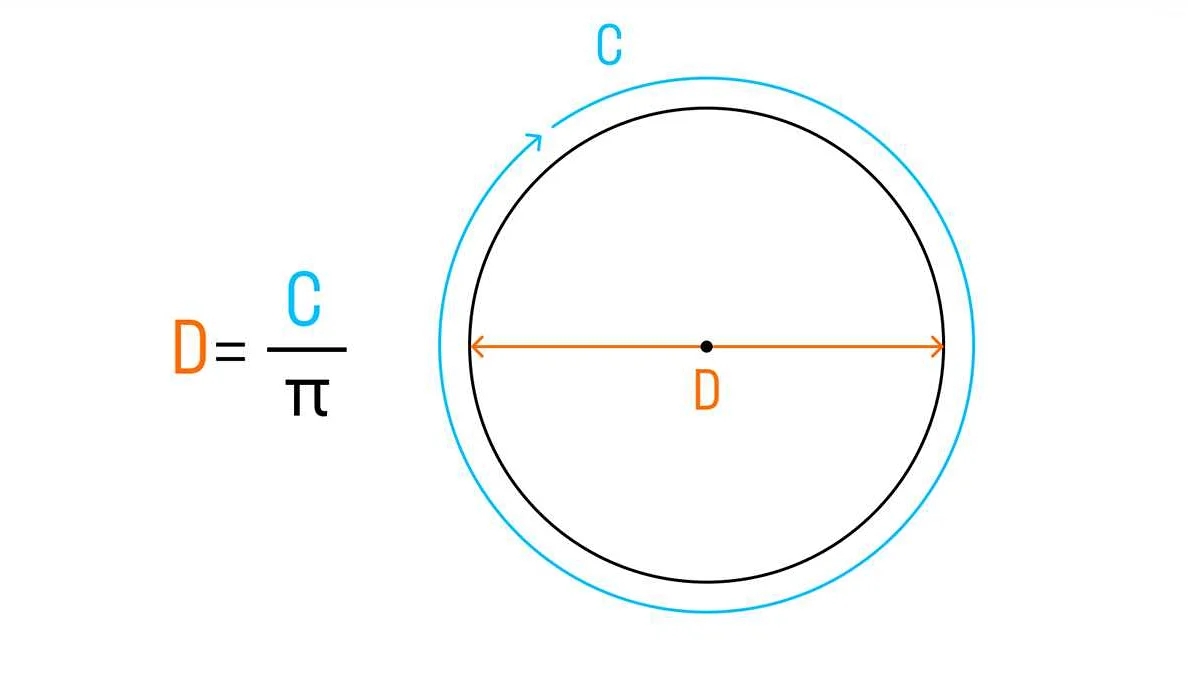
Если известна длина окружности, то диаметр можно найти, разделив длину на число Пи (π), которое примерно равно 3.14159:

ФормулаОписание

Д = L / π

Диаметр окружности равен длине окружности, разделенной на число Пи

Например, если радиус окружности равен 5 см, то диаметр будет равен 10 см. Если длина окружности равна 20 см, то диаметр будет примерно равен 6.37 см.

Таким образом, зная радиус или длину окружности, можно легко найти диаметр в математике, используя простые формулы.

Геометрическое определение диаметра в математике

Для нахождения диаметра окружности необходимо знать её радиус. Диаметр окружности равен удвоенному значению радиуса: D = 2r. Это свойство диаметра делает его одним из ключевых параметров при работе с окружностями.

Диаметр сферы также может быть определен через её радиус. Диаметр сферы равен удвоенному значению радиуса: D = 2r. Зная диаметр сферы, мы можем найти её объем, площадь поверхности и другие важные характеристики.

Для других геометрических фигур, таких как эллипс, диаметр определяется как отрезок, проходящий через его центр и соединяющий две противоположные вершины. Диаметр эллипса является важным параметром при вычислении его площади, периметра и других характеристик.

Геометрическая фигураДиаметр

Окружность	D = 2r
Сфера	D = 2r
Эллипс	Отрезок, соединяющий две противоположные вершины

В математике диаметр является важным понятием, используемым для описания и анализа геометрических фигур. Понимание геометрического определения диаметра позволяет более глубоко изучать и решать задачи, связанные с различными геометрическими объектами.

Алгебраический способ нахождения диаметра

Алгебраический способ нахождения диаметра часто используется в физике и математике для определения размеров и формы различных объектов. Для нахождения диаметра по данному способу необходимо знать другие параметры объекта, такие как его площадь или объем.

Если известна площадь поверхности объекта, то диаметр можно найти, используя следующую формулу:

1. Определите площадь поверхности объекта, которую необходимо измерить. Например, если это сфера, то площадь поверхности сферы вычисляется по формуле S = 4πr^2, где S — площадь поверхности, π — число Пи (приближенное значение 3,14), r — радиус сферы.
2. Разрешите уравнение относительно диаметра объекта. Для этого, используя формулу площади поверхности, выразите радиус через диаметр (r = D/2, где D — диаметр объекта).
3. Подставьте полученное выражение для радиуса в формулу площади поверхности и решите уравнение относительно диаметра.
4. Полученное значение диаметра будет являться результатом алгебраического способа нахождения диаметра объекта.

Этот метод нахождения диаметра основан на математических преобразованиях и может быть использован для разных геометрических фигур, включая круги, сферы и многогранники.

Как использовать диаметр в практических задачах?

В физике, диаметр может использоваться для определения площади сечения проводника, а также для расчета объема шара или цилиндра. Например, для определения площади сечения проводника, необходимо знать его диаметр и использовать формулу для площади круга.

В математике, диаметр используется для определения длины окружности и решения задач по геометрии. Например, для нахождения длины окружности, необходимо знать ее диаметр и использовать формулу длины окружности.

Диаметр также может использоваться в промышленности и инженерии для определения размеров и параметров различных объектов и механизмов. Например, для расчета прочности и напряжений в конструкции, необходимо знать диаметр используемых материалов и использовать соответствующие формулы и законы.

В заключение, диаметр — это важный параметр, который может быть использован в различных практических задачах. Знание и понимание диаметра позволяет решать задачи по физике, математике, и применять его в различных областях науки и техники.

Вопрос-ответ:

Как найти диаметр окружности?

Диаметр окружности можно найти, разделив ее длину на число пи (π).

Как найти диаметр сферы, если известен ее объем?

Для нахождения диаметра сферы по ее объему необходимо воспользоваться формулой: диаметр = (6 * объем / π)^(1/3).

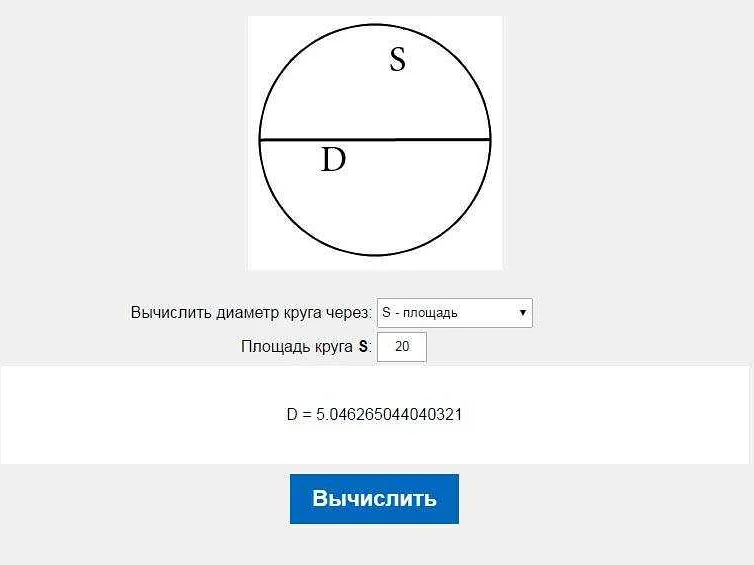
Как найти диаметр круга по его площади?

Для нахождения диаметра круга по его площади нужно воспользоваться формулой: диаметр = 2 * √(площадь / π).

Как найти диаметр шара, если известна его поверхность?

Диаметр шара можно найти, разделив поверхность шара на 4π.

Как найти диаметр окружности, если известна ее площадь?

Для нахождения диаметра окружности по ее площади нужно воспользоваться формулой: диаметр = 2 * √(площадь / π).

Видео по теме: