Что такое диаметр 3 класс математика

Диаметр в математике — это понятие, которое используется для измерения размеров геометрических фигур. В 3 классе диаметр рассматривается в контексте круга и является отрезком, соединяющим две точки на его окружности и проходящим через его центр. Познакомьтесь с понятием диаметра и его свойствами в математике.

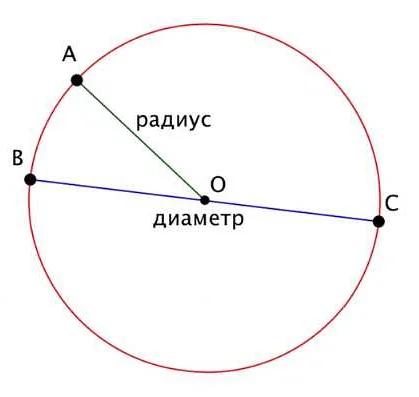
В математике диаметр является одним из основных понятий, которое учат в 3 классе. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Он является самой длинной хордой в окружности и делит ее на две равные части — полуокружности. Диаметр также определяет размеры окружности, так как его длина равна удвоенному радиусу.

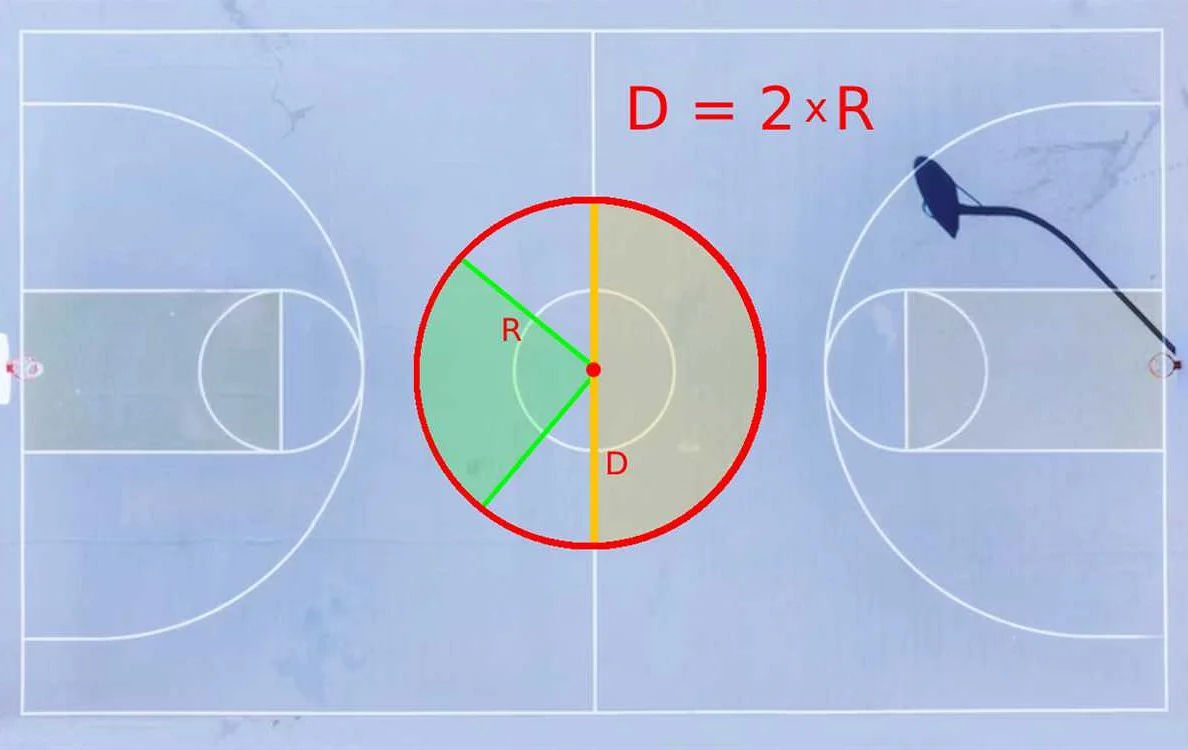
Для лучшего понимания понятия диаметра, рассмотрим пример. Представим, что у нас есть окружность с радиусом 5 см. Мы можем найти диаметр, используя формулу диаметра: Д = 2 * Р. В данном случае, диаметр будет равен 2 * 5 = 10 см. Таким образом, мы можем определить длину диаметра и его связь с радиусом.

Диаметр также играет важную роль в других математических понятиях. Например, в треугольниках, вписанных в окружность, диаметр является основанием медианы, проходящей через вершину треугольника и центр окружности. Это позволяет нам решать задачи на нахождение длины сторон и углов треугольника, используя свойства окружности и диаметра.

Итак, диаметр — это важное понятие в математике, которое помогает нам понять размеры и свойства окружности. Знание этого понятия позволяет нам решать различные задачи и применять его в других областях математики.

Что такое диаметр 3 класса математика?

В 3 классе, ученики начинают изучать основные геометрические фигуры, включая круги. Изучение диаметра круга помогает им понять, как определить его размер и свойства.

Диаметр обозначается обычно буквой d. Он равен удвоенному радиусу круга (d = 2r), где r — радиус. То есть, чтобы найти диаметр круга, нужно умножить его радиус на 2.

Например, если радиус круга равен 5 см, то его диаметр будет равен 10 см (d = 2 * 5).

Понимание диаметра круга позволяет ученикам решать задачи, связанные с измерением и построением кругов. Они могут использовать диаметр, чтобы найти длину окружности (C = πd), площадь круга (S = πr²) и другие параметры.

Важно помнить, что диаметр является прямой линией, поэтому его длина всегда больше радиуса и меньше окружности.

Зачем изучать диаметр 3 класса математика?

Изучение диаметра в 3 классе математики имеет важное значение для развития математических навыков у детей. Это понятие помогает ребенку понять сущность и свойства круга, а также научиться проводить элементарные вычисления и решать задачи.

Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Изучение диаметра помогает детям понять, что круг состоит из двух половинок, которые симметричны относительно диаметра. Также, диаметр является наибольшим отрезком, который можно провести внутри круга.

Изучение диаметра позволяет детям научиться проводить простейшие измерения. Они могут сравнивать диаметры различных окружностей и классифицировать их по их размерам. Также, дети могут измерять диаметр с помощью линейки и узнавать его величину в сантиметрах.

Знание диаметра помогает детям решать задачи, связанные с кругами. Например, они могут рассчитывать длину окружности, зная ее диаметр, или наоборот — находить диаметр, зная длину окружности. Эти навыки полезны в повседневной жизни, например, при изготовлении и измерении круглых предметов.

Примеры использования диаметра в повседневной жизни:

Изготовление и измерение колес велосипеда, автомобиля или других транспортных средств.

Изготовление и измерение крышек для банок и других контейнеров.

Разметка спортивных игровых полей, таких как футбольное или баскетбольное.

Изготовление и измерение тарелок, кружек и другой посуды.

Изготовление и измерение монет и медалей.

Определение и примеры диаметра 3 класса математика

Диаметр является наибольшим отрезком в окружности. Он делит окружность на две равные части, называемые полуокружностями.

Например, рассмотрим окружность с радиусом 5 см. Проведем через ее центр диаметр, соединяющий две точки на окружности. Длина такого диаметра будет равна 10 см.

Другой пример: окружность с радиусом 7 см. Если провести через ее центр диаметр, длина этого отрезка также будет равна 14 см.

Таким образом, диаметр в математике является особенным отрезком, который имеет связь с радиусом и центром окружности.

Как определить диаметр 3 класса математика?

Для начала нужно измерить расстояние между двумя точками на окружности. Это можно сделать с помощью школьного циркуля или линейки. Поместите одно из колес циркуля на одну точку, а другое колесо — на вторую точку. Если используется линейка, просто измерьте расстояние между этими точками.

Затем найдите половину полученного значения — это будет радиус окружности. Радиус — это расстояние от центра окружности до любой точки на ней.

Наконец, удвойте значение радиуса, чтобы получить диаметр. Диаметр — это двукратное значение радиуса.

Например, если расстояние между двумя точками на окружности составляет 6 см, радиус окружности будет 3 см, а диаметр — 6 см.

Таким образом, для определения диаметра 3 класса математика необходимо измерить расстояние между двумя точками на окружности, найти половину этого значения и удвоить его.

Примеры задач с диаметром 3 класса математика

Пример 1:

У Маши есть 5 яблок, а у Пети — на 2 яблока больше. Сколько яблок у Пети?

Решение:

Если у Маши есть 5 яблок, а у Пети на 2 яблока больше, то у Пети есть 5 + 2 = 7 яблок.

Пример 2:

На столе лежат 9 камней, а на полу — в 3 раза больше. Сколько камней на полу?

Решение:

Если на столе лежит 9 камней, а на полу в 3 раза больше, то на полу лежит 9 * 3 = 27 камней.

Пример 3:

Аня набрала 4 коробки конфет, а Миша — на 2 коробки больше. Сколько коробок конфет у Миши?

Решение:

Если Аня набрала 4 коробки конфет, а Миша на 2 коробки больше, то у Миши есть 4 + 2 = 6 коробок конфет.

Практическое применение диаметра 3 класса математика

Практическое применение диаметра может быть найдено в различных областях. Например, в архитектуре. При проектировании зданий и мостов инженеры используют понятие диаметра для определения размеров и прочности конструкций.

Еще одним примером применения диаметра является сфера спорта. В баскетболе, например, диаметр кольца, через которое игроки бросают мяч, имеет строго определенные размеры. Это позволяет установить правила игры и обеспечить равные условия для всех участников.

Диаметр также используется в географии. Например, при вычислении длин дней в разных странах. Известно, что сферическая Земля имеет диаметр, и это влияет на распределение солнечного света по поверхности планеты.

Все эти примеры демонстрируют, что понимание и применение диаметра 3 класса математики имеет важное практическое значение в различных сферах жизни.

Где можно использовать знания о диаметре 3 класса математика?

Знания о диаметре в математике могут быть применены в различных ситуациях и областях жизни, включая:

1. Геометрия: Знание диаметра позволяет понять основные понятия и свойства окружности, такие как радиус, центр, длина окружности. Он также играет важную роль в решении геометрических задач, связанных с окружностями, например, вычисление площади круга или построение равномерно распределенных точек на окружности.

2. Инженерия: Знание диаметра может быть важным при проектировании и изготовлении различных механизмов, инструментов и конструкций. Например, для правильного подбора размеров и соотношений деталей.

3. Физика: Знание диаметра может быть полезно в изучении и понимании физических явлений, связанных с окружностями, например, при рассмотрении движения тела по окружности или вращения вокруг своей оси.

4. Ежедневная жизнь: Знание диаметра может быть полезным в различных ситуациях повседневной жизни, например, при расчете размеров и выборе подходящих предметов, таких как круглый стол или шарик для игры в футбол.

Все эти примеры демонстрируют, что знание диаметра в математике является важным и полезным навыком, который может быть применен в различных сферах нашей жизни.

Вопрос-ответ:

Что такое диаметр в математике?

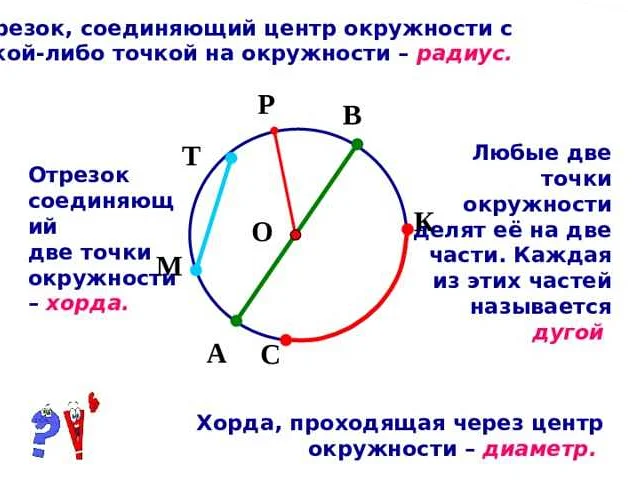
Диаметр в математике — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Он является наибольшим отрезком, который можно провести на окружности.

Как найти диаметр окружности, если известна ее длина?

Диаметр окружности можно найти, разделив ее длину на число «пи» (π), которое примерно равно 3,14. То есть формула для нахождения диаметра — это длина окружности деленная на π.

Можно ли найти диаметр окружности, если известна ее площадь?

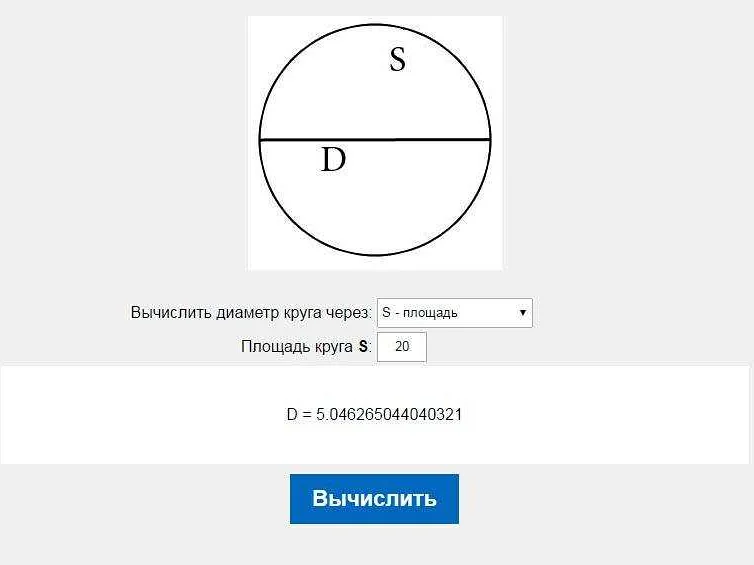
Диаметр окружности можно найти, зная ее площадь. Для этого нужно найти квадратный корень из отношения площади к числу «пи» (π) и умножить полученное значение на 2. То есть формула для нахождения диаметра — это 2 корня из площади окружности, деленной на π.

Какой пример можно привести для понимания диаметра окружности?

Примером для понимания диаметра окружности может быть, например, колесо велосипеда. Диаметр колеса — это отрезок, проходящий через центр колеса и соединяющий две его противоположные точки на ободе. Если измерить диаметр колеса, можно узнать, какая длина пути будет преодолена за один оборот колеса.

Чем отличается диаметр от радиуса?

Диаметр и радиус — это две основные характеристики окружности. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Радиус — это отрезок, соединяющий центр окружности с любой точкой на ее ободе. Диаметр в два раза больше радиуса. То есть радиус равен половине диаметра.

Что такое диаметр?

Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр.

Как найти диаметр окружности, если известна ее площадь?

Диаметр окружности можно найти, зная ее площадь, по формуле: d = 2 * sqrt(S / π), где d — диаметр, S — площадь окружности, π — число пи (приближенное значение 3,14).

Примеры задач, решение которых основано на диаметре 3 класса математика

Рассмотрим несколько примеров задач, решение которых связано с понятием диаметра в 3 классе математики.

Пример 1: В парке есть круглое озеро диаметром 15 метров. Определите его радиус.

Решение: Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Чтобы найти радиус, нужно разделить диаметр на 2. В данном случае, радиус озера будет равен 7,5 метра.

Пример 2: У Маши есть круглая тарелка диаметром 20 сантиметров. Найдите ее площадь.

Решение: Площадь круга можно найти по формуле S = π * r^2, где π — это число пи (приближенное значение 3,14), r — радиус круга. В данном случае, радиус тарелки будет равен 10 сантиметров. Подставляя значения в формулу, получим S = 3,14 * 10^2 = 314 квадратных сантиметров.

Пример 3: В школьном дворе нарисован круг с диаметром 8 метров. Найдите его длину.

Решение: Длина окружности круга можно найти по формуле L = π * d, где π — число пи, d — диаметр круга. В данном случае, диаметр равен 8 метров. Подставляя значения в формулу, получим L = 3,14 * 8 = 25,12 метров.

Таким образом, понимание понятия диаметра позволяет решать различные задачи, связанные с геометрией и измерениями. Это важное понятие помогает нам лучше понять форму и размеры окружности, используя простые математические вычисления.

Видео по теме: