Корень в математике как найти

Узнайте, как найти корень в математике и используйте различные методы, такие как извлечение квадратного корня, использование логарифмов или численные методы. Наша статья предоставляет подробные инструкции и примеры для нахождения корня любого числа.

Корень числа — это число, которое при возведении в определенную степень даёт исходное число. В математике корень выражается с помощью специального символа — радикала. На практике корень числа находят для решения различных задач, например, для нахождения неизвестного значения в уравнениях или для извлечения квадратного корня из числа.

Существует несколько методов для нахождения корня. Одним из самых простых и распространенных методов является метод подбора. Он заключается в последовательном подборе чисел, возведенных в нужную степень, до тех пор, пока не будет найдено число, при котором результат будет равен исходному числу.

Для более сложных вычислений с корнями используются другие методы, такие как метод Ньютона или итерационные методы. Они позволяют находить корни с большей точностью и в кратчайшие сроки.

Например, для нахождения квадратного корня из числа 25 можно воспользоваться методом подбора. Переберем числа от 1 до 10 и проверим, какое из них в квадрате дает 25. Оказывается, что 5 в квадрате равно 25, то есть квадратный корень из 25 равен 5.

Нахождение корней является одной из базовых операций в математике и науках, связанных с ней, таких как физика и инженерия. Умение находить корни чисел поможет в решении различных задач и упростит работу с математическими формулами и уравнениями.

Что такое корень в математике

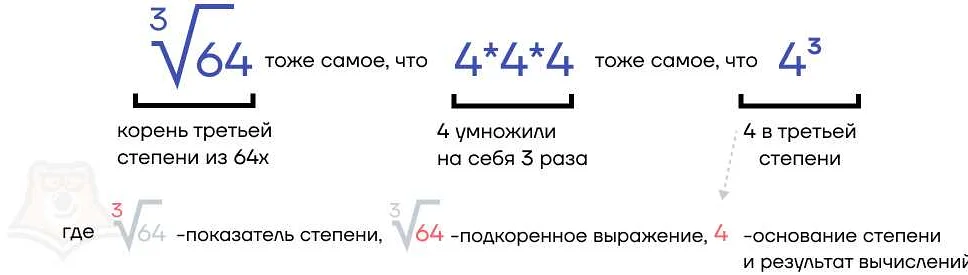
Корни могут быть как целыми числами, так и десятичными. Если корень является целым числом, то он называется целым корнем. Если корень является десятичным числом, то он называется десятичным корнем. Например, корень числа 9 является целым корнем, так как 3^2 = 9, а корень числа 2 является десятичным корнем, так как нет целого числа, возведение которого во вторую степень было бы равно 2.

Корень числа обычно обозначается символом √. Например, √4 = 2. Число под знаком корня называется радикалом. Если радикал отрицательный, то корень будет комплексным числом.

Корни имеют различные свойства и приложения в математике, физике и других научных дисциплинах. Они могут использоваться для решения уравнений, нахождения длин сторон в геометрии, анализа данных и других задач.

КореньЗначение

√4	2
√9	3
√16	4

Методы нахождения корня

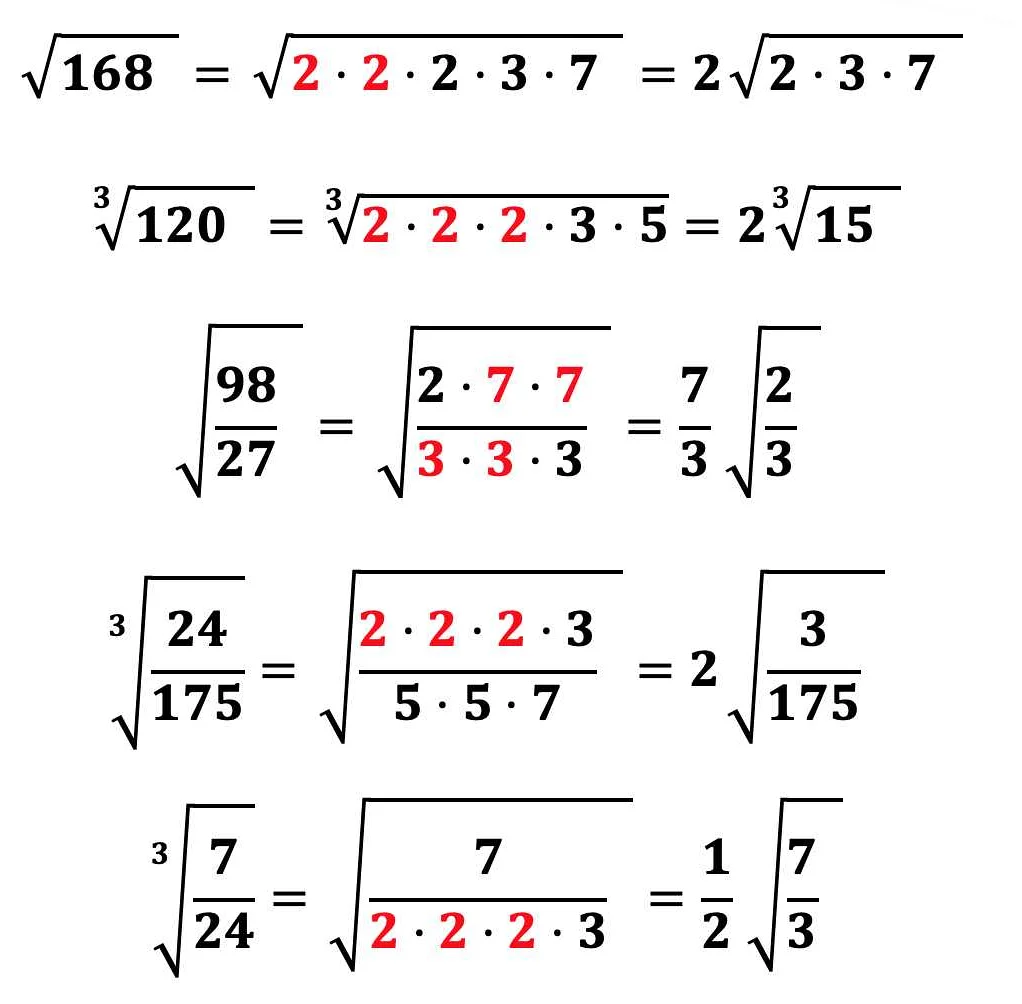
Один из самых простых методов нахождения корня — это метод итераций. Он основан на построении последовательности точек, приближающихся к искомому корню. Метод итераций широко применяется в решении уравнений и систем уравнений.

Другим распространенным методом нахождения корня является метод деления отрезка пополам. Он основан на принципе бисекции — разделении отрезка пополам и выборе половинки, в которой корень находится. Этот метод часто применяется при решении уравнений с помощью компьютерных программ.

Еще одним методом нахождения корня является метод Ньютона. Он основан на использовании производной функции и аппроксимации корня с помощью касательной линии. Метод Ньютона позволяет найти корень с высокой точностью, но требует знания производной функции.

Также существуют другие методы нахождения корня, такие как метод секущих, метод простой итерации, метод Брента и другие. Каждый метод имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи и требуемой точности.

МетодОписаниеПрименимость

Метод итераций	Построение последовательности точек, приближающихся к корню	Решение уравнений и систем уравнений
Метод деления отрезка пополам	Разделение отрезка пополам и выбор половинки с корнем	Решение уравнений с помощью компьютерных программ
Метод Ньютона	Использование производной функции и аппроксимация корня с помощью касательной линии	Нахождение корня с высокой точностью

Выбор метода нахождения корня зависит от сложности задачи и требуемой точности. Важно учитывать ограничения каждого метода и применять их в соответствии с конкретной ситуацией.

Метод простой итерации

Итерационная формула имеет вид:

xn+1 = g(xn)

где xn — текущее приближение корня, xn+1 — следующее приближение корня, g(x) — функция, определяющая зависимость между приближениями.

Процесс итераций продолжается до тех пор, пока разность между текущим и следующим приближением не станет меньше заданной точности.

Для применения метода простой итерации необходимо выполнение следующих условий:

1. Функция g(x) должна быть непрерывной на заданном интервале.
2. На этом интервале должно быть выполнено неравенство |g'(x)| < 1, где g'(x) — производная функции g(x).

Примером применения метода простой итерации может служить нахождение корня уравнения:

x2 — 4x — 10 = 0

Для этого можно представить уравнение в виде:

x = g(x) = (x2 — 10) / 4

Выберем начальное приближение, например, x0 = 0. Подставим его в итерационную формулу:

x1 = g(x0) = (02 — 10) / 4 = -10 / 4 = -2.5

Продолжаем итерационный процесс, пока не достигнем заданной точности. Например, можно остановиться, когда |xn+1 — xn| < 0.001.

Таким образом, метод простой итерации позволяет находить корни уравнений, используя последовательные приближения итерационной формулы.

Метод деления отрезка пополам

Для применения метода деления отрезка пополам необходимо исходный отрезок, на котором предполагается наличие корня, разделить на две равные части. Затем производится проверка, в какой из частей находится корень. Если значение функции меняет знак на концах отрезка, то можно сделать вывод о наличии корня в данной части.

После определения части, в которой находится корень, процесс деления отрезка пополам повторяется внутри выбранной части. Этот процесс продолжается до тех пор, пока не будет достигнута заданная точность или найдено приближенное значение корня уравнения или функции.

Метод деления отрезка пополам является простым и надежным методом нахождения корня, однако может быть неэффективным в случаях, когда корень находится вблизи одного из концов отрезка, а функция изменяет знак резко в этой области.

ШагЛевая границаПравая границаСреднее значениеЗначение функции в среднем

1	a	b	c = (a + b) / 2	f(c)
2	a	c	d = (a + c) / 2	f(d)
3	d	c	e = (d + c) / 2	f(e)
…

Приведенная таблица показывает пример шагов метода деления отрезка пополам. На каждом шаге отрезок делится пополам, а значения функции в средней точке проверяются на смену знака. Это позволяет определить, в какой части отрезка находится корень, и продолжить деление отрезка в этой части до достижения требуемой точности.

Метод Ньютона

Для применения метода Ньютона необходимо иметь начальное приближение корня уравнения. Затем, используя формулу, вычисляется следующее приближение, которое уже более точно приближается к истинному корню.

Метод Ньютона можно применять для нахождения корней различных видов функций, однако для его применения необходимо, чтобы функция была непрерывной и дифференцируемой на интервале, содержащем искомый корень.

Процесс применения метода Ньютона можно представить в виде следующей итерационной формулы:

1. Выбрать начальное приближение корня x0.
2. Вычислить следующее приближение корня xn+1 по формуле:

xn+1 = xn — f(xn) / f'(xn)

где f(xn) — значение функции в точке xn, f'(xn) — значение производной функции в точке xn.

Итерационный процесс повторяется до достижения заданной точности или выполнения других критериев остановки.

Метод Ньютона обладает хорошей сходимостью, однако он может не сойтись к корню, если начальное приближение выбрано неправильно или функция имеет особые точки, такие как разрывы или вертикальные асимптоты.

Пример применения метода Ньютона для нахождения корня уравнения:

1. Рассмотрим уравнение x2 — 4 = 0.
2. Выберем начальное приближение корня, например, x0 = 2.
3. Вычисляем следующее приближение по формуле: x1 = x0 — (x02 — 4) / (2 * x0) = 2 — (22 — 4) / (2 * 2) = 2 — (4 — 4) / 4 = 2 — 0 = 2.
4. Получаем новое приближение корня x1 = 2.
5. Повторяем шаги 3-4 до достижения заданной точности или выполнения других критериев остановки.

Таким образом, метод Ньютона позволяет приближенно находить корни уравнений с помощью итераций, основанных на использовании касательной к графику функции.

Примеры нахождения корня

Пример 1:

Найдем корень квадратный из числа 25.

Для этого можно воспользоваться методом вычисления квадратного корня, который сводится к нахождению такого числа, когда его квадрат равен 25.

Таким образом, мы ищем число x, при котором x^2 = 25. В данном случае, корнем будет число 5, так как 5^2 = 25.

Пример 2:

Найдем корень кубический из числа 8.

Для этого можно воспользоваться методом вычисления кубического корня, который сводится к нахождению такого числа, когда его куб равен 8.

Таким образом, мы ищем число x, при котором x^3 = 8. В данном случае, корнем будет число 2, так как 2^3 = 8.

Пример 3:

Найдем корень n-ой степени из числа 16.

Для этого можно воспользоваться методом вычисления корня n-ой степени, который сводится к нахождению такого числа, когда его возведенное в степень n равно 16.

Таким образом, мы ищем число x, при котором x^n = 16. В данном случае, корнем будет число 2, так как 2^4 = 16.

Таким образом, нахождение корня позволяет нам вычислять значения чисел, которые были возведены в степень или умножены на себя определенное количество раз.

Пример с использованием метода простой итерации

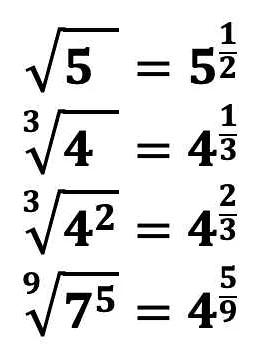
Приведем пример использования метода простой итерации для нахождения корня следующего уравнения:

Уравнение: f(x) = x^3 — 2x — 5 = 0

Для применения метода простой итерации, необходимо представить уравнение в виде x = g(x), где g(x) — некоторая функция. В данном случае, можно представить уравнение в виде:

x = (2x + 5)^(1/3)

Теперь можно начать итерационный процесс:

1. Выбираем начальное приближение корня x0
2. Вычисляем следующее приближение корня по формуле x1 = g(x0)
3. Повторяем шаг 2 до достижения необходимой точности

Предположим, что начальное приближение корня x0 = 2. Тогда, применяя формулу x1 = (2×0 + 5)^(1/3), получаем x1 ≈ 2.351.

Далее, можно продолжать итерационный процесс, вычисляя следующие приближения корня:

• x2 ≈ (2 * 2.351 + 5)^(1/3) ≈ 2.428
• x3 ≈ (2 * 2.428 + 5)^(1/3) ≈ 2.451
• x4 ≈ (2 * 2.451 + 5)^(1/3) ≈ 2.459
• и т.д.

Таким образом, продолжая итерационный процесс, можно получить все более точное приближение корня уравнения. Окончательный результат зависит от выбранного начального приближения и требуемой точности.

Метод простой итерации широко используется для нахождения корней различных уравнений, и его суть заключается в последовательном приближении к корню с помощью итерационного процесса.

Пример с использованием метода деления отрезка пополам

Рассмотрим пример нахождения корня уравнения f(x) = x^2 — 4 на интервале [1, 3].

Шаг 1: Вычисляем значение функции f(x) в точках a = 1 и b = 3:

f(a) = 1^2 — 4 = -3

f(b) = 3^2 — 4 = 5

Из полученных значений видно, что функция меняет знак на заданном интервале, что говорит о наличии корня.

Шаг 2: Делим интервал пополам и вычисляем значение функции в полученной точке:

c = (a + b) / 2 = (1 + 3) / 2 = 2

f(c) = 2^2 — 4 = 0

Значение функции в точке c равно 0, что говорит о том, что найден корень уравнения.

Шаг 3: Проверяем условие окончания метода. Если длина интервала меньше заданной точности, то останавливаемся и принимаем найденное значение за приближенный корень. В противном случае продолжаем делить интервал пополам и вычислять значение функции в полученных точках.

В данном примере мы нашли корень уравнения f(x) = x^2 — 4 на интервале [1, 3] с использованием метода деления отрезка пополам.

Вопрос-ответ:

Какие методы можно использовать для поиска корня в математике?

В математике существует несколько методов для поиска корня. Одним из самых простых и распространенных методов является метод деления отрезка пополам. Он заключается в разбиении отрезка на две равные части и последовательном сужении интервала поиска до тех пор, пока не будет достигнута необходимая точность. Другим методом является метод Ньютона, который основан на линейном приближении функции и последовательном уточнении корня. Еще одним методом является метод итераций или метод простых итераций, который основан на нахождении неподвижной точки функции. Это лишь некоторые из множества методов, используемых для поиска корня в математике.

Как работает метод деления отрезка пополам?

Метод деления отрезка пополам заключается в разбиении отрезка на две равные части и проверке, в какой из них находится корень функции. Если на отрезке есть корень, то он будет либо в одной из двух половинок, либо совпадать с их границей. После того как определена половинка, в которой находится корень, процесс деления отрезка пополам повторяется для этой половинки. Таким образом, отрезок постепенно сужается до тех пор, пока не будет достигнута необходимая точность. В результате получается приближенное значение корня.

Как работает метод Ньютона для поиска корня?

Метод Ньютона для поиска корня основан на линейном приближении функции и последовательном уточнении корня. Сначала выбирается начальное приближение корня. Затем, используя значение функции и ее производной в этой точке, вычисляется следующее приближение корня с помощью формулы x(n+1) = x(n) — f(x(n))/f'(x(n)), где x(n) — текущее приближение, f(x(n)) — значение функции в точке x(n), f'(x(n)) — значение производной функции в точке x(n). Этот процесс повторяется до достижения необходимой точности. Метод Ньютона является итерационным методом и обычно сходится очень быстро.

Как найти корень квадратный из числа?

Для того чтобы найти квадратный корень из числа, нужно найти число, когда его квадрат будет равен данному числу. Например, если вам нужно найти квадратный корень из числа 16, нужно найти число, которое, возведенное в квадрат, даст 16. В данном случае, квадратный корень из 16 равен 4, так как 4 * 4 = 16.

Как найти корень из отрицательного числа?

Корень из отрицательного числа невозможно найти в обычных вещественных числах, так как квадрат любого числа всегда положителен. Однако, в математике существует понятие комплексных чисел, которые позволяют находить корни из отрицательных чисел. Например, квадратный корень из -1 равен мнимой единице i, так как i * i = -1.

Пример с использованием метода Ньютона

xn+1 = xn — f(xn) / f'(xn),

где f(x) — функция, f'(x) — ее производная, xn — текущее приближение корня, xn+1 — следующее приближение корня.

Рассмотрим пример нахождения корня квадратного уравнения x2 — 4 = 0 с использованием метода Ньютона.

nxnxn+1

0	2	1.5
1	1.5	1.4167
2	1.4167	1.4142
3	1.4142	1.4142

В таблице представлены значения приближений корня на каждой итерации. Начальное приближение x0 выбрано равным 2. Значения xn+1 на каждой итерации получены с помощью формулы метода Ньютона. Последовательность приближений сходится к значению корня, которое равно 1.4142. Таким образом, найденное значение является приближенным корнем исходного уравнения.

Видео по теме: