Корень в математике что это

Корень в математике — это операция, обратная возведению в степень. Он позволяет найти число, которое при возведении в указанную степень даёт исходное число. Узнайте больше о понятии корня в математике и его свойствах.

Математика — это наука о числах и их свойствах. Одним из основных понятий в математике является корень. Корень — это число, умноженное само на себя, чтобы получить исходное число. Например, корнем числа 9 является число 3, так как 3 умноженное на 3 равно 9.

Вычисление корня — это процесс нахождения числа, которое при возведении в квадрат даст заданное число. Существуют различные способы вычисления корня, в зависимости от степени корня и точности результата. Одним из наиболее распространенных методов является метод Ньютона, также известный как метод касательных.

Метод Ньютона заключается в последовательном приближении к искомому корню с помощью линейной аппроксимации. Он основывается на идее, что касательная к графику функции в точке пересечения ее с осью абсцисс будет приближением к искомому корню.

Вычисление корня может быть полезным во многих областях, таких как физика, инженерия, экономика и компьютерная наука. Знание методов и приемов вычисления корня позволяет решать широкий спектр задач и делает математику одним из ключевых инструментов для анализа и моделирования различных явлений.

Что такое корень в математике?

Корень обозначается символом √, перед которым пишется число, из которого вычисляется корень. Например, √25 равно 5, так как 5 в квадрате равно 25.

Корни называются по степени, которую они извлекают. Например, корень квадратный – это корень степени 2, корень кубический – это корень степени 3.

Вычисление корня в математике можно выполнить с помощью таблицы корней или с использованием специальных формул и алгоритмов.

КореньОбозначениеПример

Квадратный корень	√	√25 = 5
Кубический корень	∛	∛27 = 3
Корень четвертой степени	∜	∜16 = 2

Вычисление корня может быть положительным или отрицательным. Корень из отрицательного числа обозначается символом √ с нижним индексом, указывающим на то, что число отрицательное. Например, √-4 = 2i, где i – мнимая единица.

Корни в математике широко используются в различных научных и инженерных областях, а также в повседневной жизни для решения задач и вычислений.

Понятие и определение корня

Корни могут быть как рациональными (целыми или десятичными), так и иррациональными (непериодическими десятичными дробями или бесконечными десятичными дробями). Например, корень из 4 равен 2, а корень из 2 — это иррациональное число, обозначаемое символом √2.

Основные свойства корней:

• Корень из произведения равен произведению корней: √(a * b) = √a * √b
• Корень из частного равен частному корней: √(a / b) = √a / √b
• Корень из числа в степени равен числу, возведенному в степень, деленному на показатель корня: √(an) = an/n

Корни широко используются в различных областях математики и науки, таких как алгебра, геометрия, физика и т.д. Вычисление корней позволяет решать разнообразные задачи, включая поиск решений уравнений, определение значений переменных и т.д.

Различные типы корней

В математике существуют различные типы корней:

• Квадратный корень — это число, которое при возведении в квадрат дает исходное число. Например, квадратный корень из числа 9 равен 3, так как 3 * 3 = 9.
• Кубический корень — это число, которое при возведении в куб дает исходное число. Например, кубический корень из числа 8 равен 2, так как 2 * 2 * 2 = 8.
• Корень любой степени — это число, которое при возведении в соответствующую степень дает исходное число. Например, корень четвертой степени из числа 16 равен 2, так как 2 * 2 * 2 * 2 = 16.

Вычисление корня может быть выполнено с использованием специальных математических функций или методов, которые позволяют найти значение корня числа.

Значение корня в математических выражениях

Значение корня в математических выражениях можно вычислить с помощью специальных формул и алгоритмов. Для этого необходимо знать основные свойства корней и уметь применять алгоритмы вычисления корня.

Основные свойства корней:

• Корень из суммы равен сумме корней: √(а + b) = √a + √b
• Корень из разности равен разности корней: √(а — b) = √a — √b
• Корень из произведения равен произведению корней: √(а * b) = √a * √b
• Корень из частного равен частному корней: √(а / b) = √a / √b

Для вычисления значения корня в математических выражениях необходимо выполнить следующие шаги:

1. Раскрыть скобки, если они есть.
2. Применить основные свойства корней для упрощения выражения.
3. Вычислить значения корней, используя алгоритмы вычисления корня.

Вычисление корня из числа может быть выполнено ручным методом или с использованием калькулятора или специальных программ. В случае сложных выражений рекомендуется использовать калькулятор или программу для более точного и быстрого вычисления корня.

Как вычислить корень?

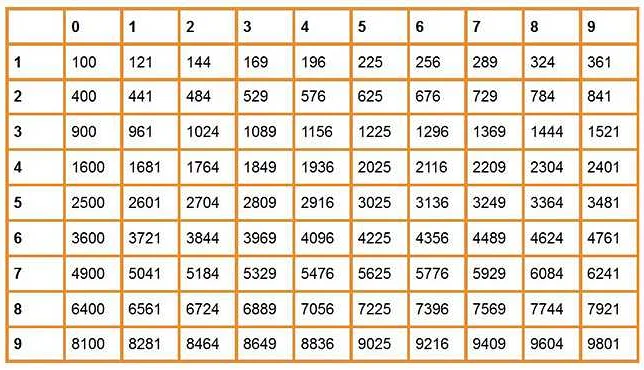
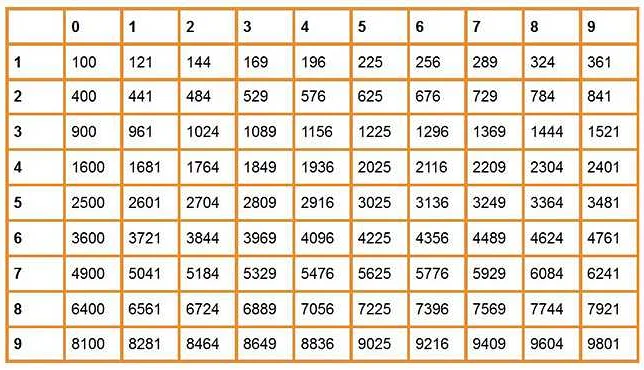
Существует несколько способов вычисления корня. Один из них — это использование калькулятора. В большинстве калькуляторов есть функция квадратного корня, которая позволяет вычислить корень из заданного числа. Для этого нужно просто ввести число и нажать на кнопку с символом √.

Если у вас нет калькулятора под рукой или вы хотите вычислить корень вручную, можно воспользоваться методом Ньютона. Этот метод заключается в последовательном приближении к корню с использованием итераций. Для вычисления квадратного корня числа a можно использовать следующую формулу: xn+1 = (xn + a/xn)/2, где xn — приближение к корню на n-й итерации.

Другой способ вычисления корня — это использование таблицы квадратных корней. В такой таблице приведены значения корней различных чисел. Для вычисления корня из числа, вы ищете в таблице ближайшее значение и интерполируете остальные значения.

Независимо от способа вычисления корня, важно помнить, что результат может быть представлен как положительное, так и отрицательное число. Например, корень из 9 может быть равен как 3, так и -3. Поэтому при вычислении корня часто используется знак ∓, который обозначает оба значения корня.

Методы вычисления корня

1. Метод простых итераций:

Этот метод основан на постепенном приближении к корню путем итераций. Для вычисления корня уравнения f(x) = 0, сначала нужно уравнение привести к виду x = g(x), где g(x) — функция, зависящая только от переменной x. Затем выбирается начальное приближение x0 и осуществляются последовательные итерации по формуле xn+1 = g(xn), пока не будет достигнута необходимая точность.

2. Метод деления отрезка пополам:

Для нахождения корня на отрезке [a, b] можно использовать метод деления отрезка пополам. Суть метода заключается в следующем: сначала вычисляется значение функции f(x) в середине отрезка (a + b)/2. Затем определяется, в какой половине отрезка находится корень. Если f(x) = 0, то корень найден. Если f(x) имеет разные знаки на концах отрезка, то корень находится в одной из половин отрезка. Процесс разделения отрезка продолжается до достижения необходимой точности.

3. Метод Ньютона:

Метод Ньютона основан на использовании производной функции f(x) для приближенного вычисления корня. Сначала выбирается начальное приближение x0. Затем осуществляются последовательные итерации по формуле xn+1 = xn — f(xn)/f'(xn), где f'(xn) — производная функции f(x) в точке xn. Процесс продолжается до достижения необходимой точности.

4. Метод Брента:

Метод Брента сочетает в себе методы деления отрезка пополам и Ньютона. Он действует похожим на метод деления отрезка пополам образом, но при необходимости использует метод Ньютона для ускорения сходимости. Метод Брента является одним из наиболее эффективных методов для вычисления корня.

Использование калькулятора для вычисления корня

Одним из способов вычисления корня числа является использование метода итераций. Для этого необходимо сначала выбрать значение, которое будет приближенным корнем числа. Затем, используя определенную формулу, можно последовательно уточнять это приближенное значение, пока не будет достигнута нужная точность.

Калькуляторы с функцией извлечения квадратного корня позволяют вычислить корень числа быстро и без особых сложностей. Для этого необходимо ввести число, нажать соответствующую кнопку на калькуляторе, и результат будет выведен на экран. Если требуется вычислить корень с показателем отличным от двух, многие калькуляторы имеют функцию возведения в степень, с помощью которой можно реализовать вычисление таких корней. В этом случае необходимо сначала ввести значение, затем нажать кнопку возведения в степень, затем ввести показатель степени и, наконец, нажать кнопку извлечения корня.

Примеры калькуляторов с функцией извлечения корня:

1. Casio fx-991ES

2. Texas Instruments TI-30X IIS

3. Sharp EL-W516XBSL

Практические примеры вычисления корня

Вот несколько простых примеров, чтобы продемонстрировать, как вычислить корень числа:

Число	Корень
4	2
9	3
16	4
25	5

Как видно из таблицы, чтобы найти корень числа, нужно найти число, которое при возведении в квадрат дает исходное число. Например, корень числа 4 равен 2, потому что 2^2 = 4.

Пример вычисления квадратного корня

Представим, что нам нужно вычислить квадратный корень числа 16. Для этого существует несколько способов.

• Способ 1: Метод итераций
  1. Выбираем начальное приближение. Допустим, что это число 4.
  2. Вычисляем новое приближение, используя формулу: новое_приближение = (старое_приближение + (число / старое_приближение)) / 2
  3. Повторяем шаг 2 до тех пор, пока разница между старым и новым приближениями не станет достаточно малой.
• Способ 2: Использование встроенных функций
  1. Воспользуйтесь встроенной функцией в вашем языке программирования, которая вычисляет квадратный корень.

В результате вычисления квадратного корня числа 16 по обоим способам мы получим ответ 4.

Пример вычисления кубического корня

Кубический корень числа можно вычислить с помощью специальной математической функции или с использованием алгоритма.

Рассмотрим пример вычисления кубического корня числа 27.

С помощью математической функции:

Кубический корень из 27 равен 3, так как 3 * 3 * 3 = 27.

С помощью алгоритма:

1. Задаем начальное приближение для кубического корня, например, 2.

2. Пока квадрат текущего приближения не станет достаточно близким к исходному числу, выполняем следующие шаги:

а) Вычисляем новое приближение как среднее арифметическое между текущим приближением и исходным числом, деленным на квадрат текущего приближения.

б) Повторяем шаг а) до достижения необходимой точности.

По алгоритму кубический корень из 27 также равен 3.

Вопрос-ответ:

Что такое корень в математике?

Корень в математике — это число, которое при возведении в некоторую степень даёт другое число.

Как вычислить корень из числа?

Корень из числа можно вычислить с помощью специальной функции в математических программированиях, таких как Python. Например, для вычисления квадратного корня можно использовать функцию sqrt().

Как найти корень из числа без использования калькулятора?

Если число является точным квадратом, то его корень можно найти путем извлечения корня. Если число не является точным квадратом, то для нахождения корня можно использовать приближенные методы, такие как метод Ньютона.

Зачем нужны корни в математике?

Корни в математике используются для решения уравнений, нахождения длин сторон треугольников, вычисления площадей и объемов фигур, и многих других задач.

Какова связь между корнями и степенями в математике?

Корень и степень в математике являются взаимообратными операциями. Корень из числа a — это число, возведение которого в степень n дает a. И наоборот, возведение числа в некоторую степень n равно корню из этого числа.

Что такое корень в математике?

Корень в математике — это операция, обратная возведению числа в степень. Если число a возвести в степень n, то корень из этого числа — это такое число x, что x в степени n равно a.

Видео по теме: