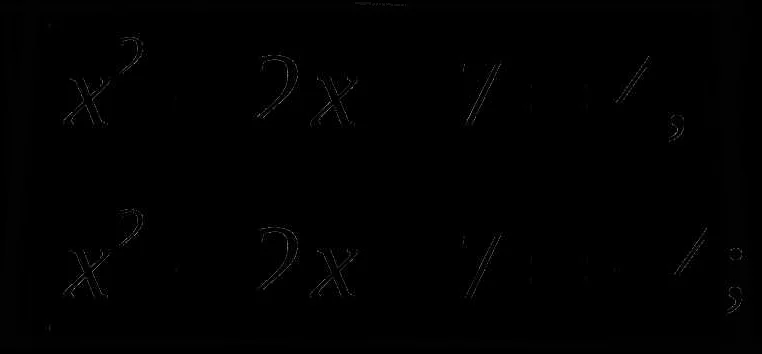Как работать с квадратными скобками в математике: система неравенств

Узнайте, что означают квадратные скобки в математике в системе неравенств. Научитесь интерпретировать математические выражения и применять их в задачах.

В математике квадратные скобки имеют специальное значение и обозначают интервал чисел. Например, [3, 7] означает интервал от 3 до 7, включая граничные значения. Если же вы видите скобки со знаком «>» или »

Решая систему неравенств, необходимо учитывать, какие знаки стоят перед квадратными скобками. Если стоит знак «>» или «>=», то граничное значение включается в решение, тогда как при «x x >= 2» означает, что x может быть любым числом от 2 до 5, не включая 5. Если бы неравенство было «x < 5″ и «x > 2″, то решение системы было бы интервалом от 2 до 5, включая оба края.

Чтобы решить систему неравенств, нужно определить пересечение интервалов, заданных каждым неравенством. Если интервалы пересекаются, то они образуют решение системы. Если же интервалы не пересекаются, то решений системы нет.

Квадратные скобки в математике могут вводить в заблуждение, поэтому имейте в виду, что их использование может менять результат решения задачи.

Квадратные скобки в математике: что означают?

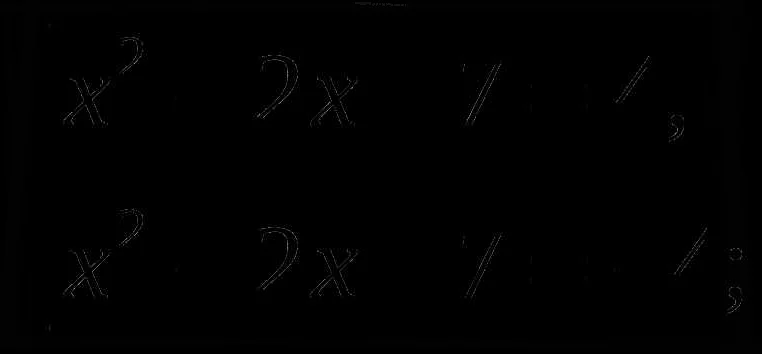
Квадратные скобки в математике используются для указания диапазона чисел или элементов в матрице, векторе или множестве. Они также могут использоваться для обозначения округления числа до ближайшего целого числа.

Для обозначения диапазона чисел квадратные скобки используются с числами, например, [1, 5] обозначает диапазон чисел от 1 до 5, включая 1 и 5. Если квадратные скобки заменить на круглые скобки, то это будет означать диапазон чисел с 1 и 5, не включая их.

Кроме того, квадратные скобки могут использоваться для обозначения элементов в матрице и векторе. Например, A[1,2] обозначает элемент матрицы, находящийся в первой строке и втором столбце.

Квадратные скобки также используются для обозначения множества, например, S = [1, 2, 3, 4, 5] обозначает множество, состоящее из чисел 1, 2, 3, 4, и 5.

В заключение, квадратные скобки в математике имеют много назначений и используются для разных операций и вычислений. Необходимо следить за их использованием для правильного вычисления и решения математических задач.

Видео по теме:

Обозначение диапазона значений

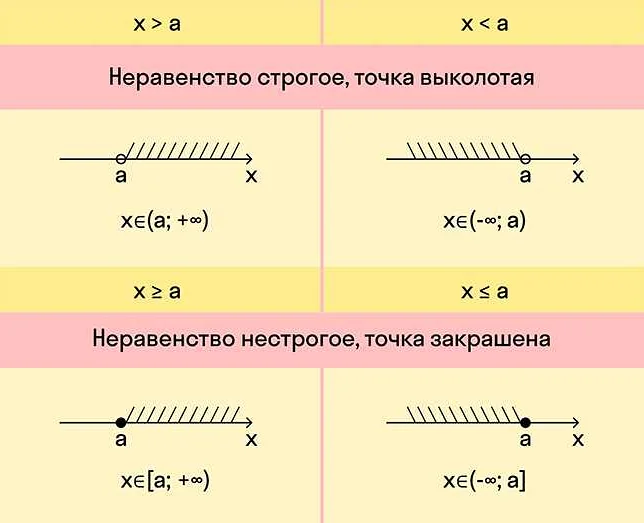
В математике часто используются квадратные скобки для обозначения диапазона значений. Например, [a,b] означает множество всех чисел, которые больше или равны a и меньше или равны b. Если же мы используем круглые скобки, то это уже означает, что крайние числа не включаются в этот диапазон. То есть (a,b) обозначает множество всех чисел, которые больше a и меньше b.

Например, если мы решаем систему уравнений или неравенств и получаем, что x должен лежать в диапазоне [1,5], то это означает, что x может принимать значения от 1 до 5 включительно. Если же мы получаем, что x должен лежать в диапазоне (1,5), то это означает, что x может принимать значения от 1 до 5, но 1 и 5 не включаются в этот диапазон.

Кроме квадратных и круглых скобок, в математике также используются фигурные скобки, которые обычно используются для обозначения множества. Например, {1, 2, 3} обозначает множество, состоящее из трех элементов: 1, 2 и 3.

Для более сложных диапазонов или промежутков могут использоваться другие обозначения, например, (a,∞) обозначает множество всех чисел, больших a, или [0,1) обозначает множество всех чисел, которые больше или равны 0, но меньше 1.

Округление до целого числа

Округление — это процесс приведения числа к ближайшему значению из заданного множества чисел. Округление до целого числа является наиболее распространенным видом округления.

Для округления числа до целого значения в математике используются следующие правила:

• Если дробная часть числа меньше 0,5, то число округляется до ближайшего меньшего целого числа.
• Если дробная часть числа больше или равна 0,5, то число округляется до ближайшего большего целого числа.

Например, число 4,6 будет округлено до 5, а число 3,2 будет округлено до 3.

В программировании округление до целого числа может быть выполнено с помощью функций round(), floor() и ceil() языков программирования. Функция round() округляет число до ближайшего целого числа; floor() округляет число до ближайшего меньшего целого числа; ceil() округляет число до ближайшего большего целого числа.

Важно помнить, что округление может приводить к потере точности, поэтому необходимо использовать его с осторожностью. Также стоит учитывать, что округление может быть необходимо в различных ситуациях, например, при оформлении отчетов, при работе с финансовыми данными и т.д.

Округление до определенной степени

Округление чисел — это процесс приведения значения числа к более простому виду или увеличению точности. В математике, для округления чисел используются различные методы, включая округление до ближайшего целого, округление до ближайшего десятка или сотни и т.д.

Округление до определенной степени — это процесс, при котором число округляется до ближайшего значения, кратного определенной степени. Например, если мы округляем число 26 до ближайшей десятки, то получим 30, так как 30 кратно 10, а 26 нет.

Чтобы округлить число до определенной степени, нужно следовать определенному правилу. Если число, которое нужно округлить, заканчивается цифрой 0, 1, 2, 3, или 4, то округляется до ближайшего меньшего числа, которое кратно указанной степени.

Если число, которое нужно округлить, заканчивается цифрами 5, 6, 7, 8, или 9, то округляется до ближайшего большего числа, которое кратно указанной степени.

• Например, если мы хотим округлить число 34 до ближайшей десятки, то получим 30, так как 34 находится ближе к 30, чем к 40
• Но если мы хотим округлить число 38 до ближайшей десятки, то получим 40, так как 38 находится ближе к 40, чем к 30.

Округление до определенной степени используется в различных областях, включая финансы, статистику и науку в целом, где точность играет важную роль и все результаты должны быть округлены до определенной степени.

Классификация остатков по модулю

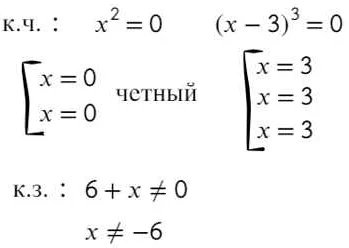
При работе с модулями в математике важно понимать, что каждое число имеет свой остаток при делении на модуль. Остаток может быть положительным, отрицательным или равным нулю.

Для классификации остатков по модулю используется термин «вычет». Вычеты делятся на две категории: приведенные и неприведенные.

• Приведенные вычеты — это остатки, которые находятся в интервале от 0 до модуля-1. Например, если модуль равен 7, то приведенные вычеты будут иметь значения от 0 до 6.
• Неприведенные вычеты — это остатки, которые больше или меньше интервала приведенных вычетов. Например, если модуль равен 7, то неприведенными будут все остатки, которые меньше 0 или больше 6.

Остатки по модулю важны при решении уравнений и систем неравенств, а также в теории чисел.

Кроме того, для классификации вычетов по модулю используется понятие «взаимно простых чисел». Если два числа не имеют общих делителей, кроме 1, то они считаются взаимно простыми. При работе с остатками по модулю важно учитывать, что взаимно простые числа дают разные вычеты по модулю.

Как решать систему неравенств с квадратными скобками?

Система неравенств с квадратными скобками решается так же, как и система с обычными круглыми скобками. Однако, необходимо учитывать особенности области определения переменных.

Если в системе присутствуют неравенства вида [a,b], то это означает, что переменная может принимать значения от a до b включительно. Если неравенство имеет вид (a,b), то переменная может принимать значения от a до b не включительно.

При решении системы с двумя переменными необходимо найти пересечение областей, определенных каждым уравнением. Это пересечение и будет являться решением системы.

Если в системе присутствует только одно уравнение с квадратными скобками, то его можно преобразовать к виду с обычными скобками, заменив квадратные скобки на знаки больше или меньше в зависимости от знака неравенства.

Например, систему уравнений:

x + 2[y-3] ≤ 7

3x — [y-2] ≤ 8

можно решить следующим образом:

1. 1. Преобразуем первое уравнение:

x + 2y — 6 ≤ 7

x + 2y ≤ 13

1. 1. Преобразуем второе уравнение:

3x + 2 — y ≤ 8

3x — y ≤ 6

1. 1. Перепишем оба уравнения в виде «y ≤ …» и «y ≥ …»:

y ≤ -x/2 + 13/2

y ≥ 3x — 6

1. 1. Найдем пересечение областей определения для y:

-x/2 + 13/2 ≥ 3x — 6

x ≤ 7/5

3x — 6 ≤ -x/2 + 13/2

x ≤ 8/5

1. 1. Получаем решение системы:

0 ≤ x ≤ 8/5

-x/2 + 13/2 ≥ y ≥ 3x — 6

Основные правила решения систем неравенств

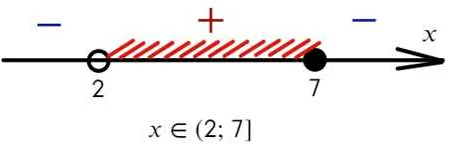
1. Определение переменных. Для решения систем неравенств необходимо определить значение каждой переменной, которое мы ищем. Обычно переменные обозначают буквами x, y, z и т.д.

2. Выражение условий. Формулируем условия каждого неравенства в системе через выбранные переменные. Неравенства могут содержать знаки «больше», «меньше», «больше или равно», «меньше или равно» и т.д.

3. Графическое представление. Представляем каждое неравенство графически на координатной плоскости, что позволяет определить области, где выполняются соответствующие неравенства.

4. Определение решения системы. По полученной графической информации определяем общую область решений системы неравенств. Для этого находим пересечение всех областей, соответствующих каждому из неравенств в системе. Обычно это зона на плоскости, которая покрывается всеми штриховками, проведенными на графиках неравенств.

5. Проверка решения. После определения общей области решений проверяем, что решения подходят под все условия системы неравенств. Для этого подставляем координаты произвольной точки из полученной общей области решений в каждое неравенство системы. Если все неравенства выполняются, то решение системы верно.

Следуя этим правилам, мы можем решить систему неравенств и определить множество значений переменных, при которых все условия системы выполняются.

Учет особенностей при нахождении корней

При решении систем неравенств или уравнений, в которых присутствуют квадратные скобки, необходимо учитывать некоторые особенности, связанные с определением корней.

Во-первых, необходимо помнить, что открытые и закрытые скобки влияют на знак неравенства. Если скобка открывается вправо, то знак неравенства меняется на противоположный. Если же скобка закрывается вправо, то знак неравенства остается прежним.

Во-вторых, стоит учитывать, что скобки могут быть как положительными, так и отрицательными. При этом, если важен только знак, то можно убрать скобки и помнить, что отрицательные скобки изменяют знак неравенства, а положительные сохраняют его.

Иногда может возникнуть ситуация, когда есть несколько корней, и нужно найти наибольшее или наименьшее из них. В этом случае, можно составить таблицу значений и перебрать все возможные комбинации корней, определяя, какой из них наибольший или наименьший.

Важно помнить, что при нахождении корней в системах неравенств с квадратными скобками, нужно быть внимательным и аккуратным, особенно когда речь идет о решении комплексных неравенств.

Примеры решения систем неравенств с квадратными скобками

Системы неравенств с квадратными скобками похожи на системы с круглыми скобками, но имеют несколько особенностей, которые необходимо учитывать при их решении. Рассмотрим несколько примеров:

• • Пример 1:

[2, 5] x (1, 4] = ?

• Решение:

Для начала, перепишем данную систему в виде двух отдельных неравенств:

2 ≤ x ≤ 5

1 < x ≤ 4

Чтобы найти решение системы, нужно найти пересечение множеств, заданных каждым из неравенств. В данном случае, это множество [2, 4]. Однако, это не полный ответ, так как второе условие (1 < x) не учитывается в этом интервале. Итак, окончательный ответ:

x ∈ [2, 4], x > 1

• • Пример 2:

[-3, 2] ∪ [5, 8) = ?

• Решение:

Данная система состоит из двух интервалов, которые нужно объединить. Множество [-3, 2] означает все числа от -3 до 2 включительно, а множество [5, 8) — все числа от 5 до 8, не включая 8. Таким образом, объединив эти множества, получаем:

x ∈ [-3, 2] ∪ [5, 8)

• • Пример 3:

(-∞, -2) ∩ [-3, 5] = ?

• Решение:

Здесь нужно найти пересечение двух множеств: (-∞, -2) и [-3, 5]. Множество (-∞, -2) означает все отрицательные числа, меньшие -2, а множество [-3, 5] — все числа от -3 до 5 включительно. Ответ:

x ∈ [-3, -2)

Дополнительные полезные материалы

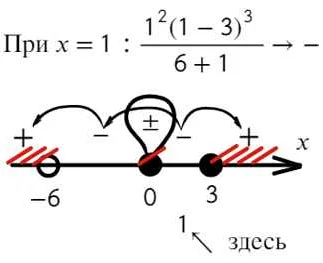
Для более глубокого понимания квадратных скобок в математике и их использования рекомендуется обратиться к учебникам по алгебре, геометрии и математическому анализу. В них можно найти различные примеры задач, основанных на использовании квадратных скобок и систем неравенств. Также стоит обратить внимание на разделы, посвященные операциям с числами и алгебраическим выражениям.

Для более подробного изучения систем неравенств и их решения с помощью квадратных скобок рекомендуется обратиться к специализированным математическим книгам. В таких книгах можно найти более сложные задачи и теоретические аспекты, связанные с решением систем неравенств.

Для тех, кто хочет практиковать решение задач с использованием квадратных скобок, рекомендуется обратиться к онлайн-ресурсам по математике. Такие ресурсы предлагают различные задания и тесты, которые помогут закрепить пройденный материал и улучшить свои навыки в решении задач.

Важно также помнить, что знание квадратных скобок и систем неравенств пригодится не только в школьной программе, но и в жизни. Например, при решении задач, связанных с планированием бюджета и расчетом финансовых вложений.

Советы по работе с системами неравенств с квадратными скобками

Системы неравенств с квадратными скобками могут вызывать затруднения при решении, но есть несколько советов, которые могут помочь в их решении.

• Правила знаков: в системах неравенств с квадратными скобками стоит обратить внимание на правила знаков. Если неравенство содержит инвертированный знак, то следует поменять знак неравенства и изменить знак скобок. Например, если у нас есть неравенство [-2, 4) = x > (7, 3], что упрощает работу с неравенством.
• Правильное определение интервалов: для решения системы неравенств с квадратными скобками необходимо понимать, какие интервалы обозначаются квадратными или круглыми скобками. Квадратные скобки обозначают замкнутые интервалы, т.е. справа и слева включают границы интервала, а круглые скобки обозначают открытые интервалы, т.е. справа и слева исключают границы интервала.
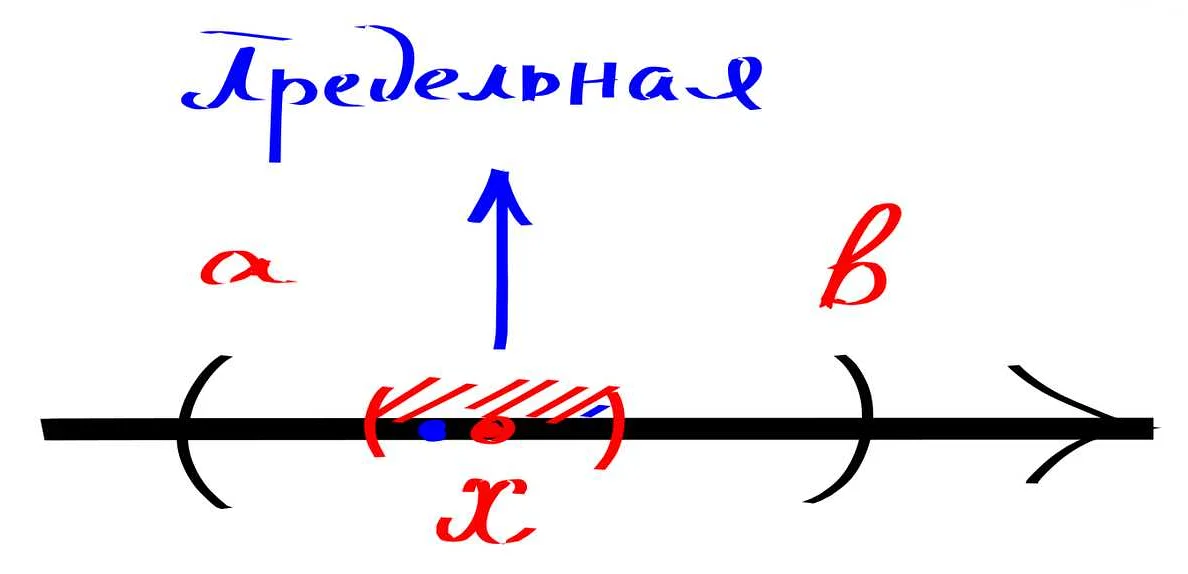
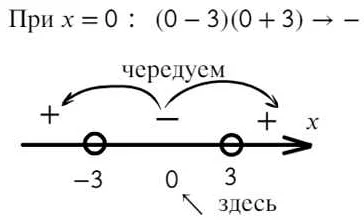
• Графическое представление: для наглядности и лучшего понимания системы неравенств с квадратными скобками можно проиллюстрировать их графическим представлением на числовой оси. Это позволяет лучше представить, какие числа входят в искомый интервал и как они расположены относительно друг друга.
• Систематический подход: при решении системы неравенств с квадратными скобками следует использовать систематический подход, начиная с определения интервалов каждого неравенства, далее находим пересечение этих интервалов и определяем итоговый интервал, в котором искомое значение лежит.

Соблюдение этих советов поможет упростить работу с системами неравенств с квадратными скобками и повысить точность решения. Не стоит спешить при решении таких систем, а следует тщательно проверять все условия и правильно определять интервалы, чтобы избежать ошибок в решении.

Вопрос-ответ:

Какие значения могут быть в квадратных скобках в системе неравенств?

В квадратных скобках могут быть указаны граничные значения интервала, которые включаются в решение системы. Например, если в неравенстве [2, 5]x < 10 справа число 10 включено в диапазон, то решение будет x ≤ 5, а если было бы (2, 5]x < 10, то решение составило бы x < 5.

Каким образом квадратные скобки отличаются от круглых в математике?

Круглые скобки просто обозначают порядок операций, тогда как квадратные скобки имеют специализированное применение — они описывают границы диапазона или интервала, включая или исключая их. Например, (2 + 3) x 4 означает 5 x 4, а [2, 4]x означает x, который может быть от 2 до 4 включительно.

Как решать систему неравенств, где присутствуют квадратные скобки?

Для решения системы неравенств с квадратными скобками необходимо понимать правила алгебры неравенств и работать с интервалами значений переменных. В целом, для решения системы нужно сначала переписать её в более компактной форме и затем применять известные методы алгебры для нахождения значения переменной. В общем случае решение может быть несколько сложнее, чем при обычных неравенствах.

Как определить, включаются или исключаются границы диапазона в квадратных скобках?

Указание скобок может быть разной и зависит от контекста. Если вместо квадратных скобок используются круглые скобки или знаки >..< и , то границы диапазона не включаются в решение. Если используются квадратные скобки, то границы диапазона включены в решение. Важно обратить внимание, на данную информацию при решении системы неравенств.

Можно ли использовать круглые скобки вместо квадратных для обозначения диапазона в системе неравенств?

Нет, замена квадратных скобок круглыми в системе неравенств может привести к некорректному решению, т.к. формулировка задачи изменится. Если в задаче явно указаны скобки, то вы исключите границы диапазона из возможных решений. Изменения задачи может привести к изменению решений системы неравенств.

Что нужно знать о границах диапазона при решении системы неравенств?

Границы диапазона могут включаться или исключаться в соответствии с правилами записи диапазона. Включая скобки в решение системы неравенств, вам необходимо учитывать их смысловую нагрузку и использовать правильные знаки, понимающие, оставлять границы диапазона или нет в возможных решениях.

Какие правила необходимо учитывать при работе с квадратными скобками?

При использовании квадратных скобок необходимо помнить следующее: [] — границы включаются в решение; () — границы не включаются в решение; [) — начальная граница включена, конечная граница исключена из решения, (; ] – начальная граница исключена, конечная граница включена в решение.