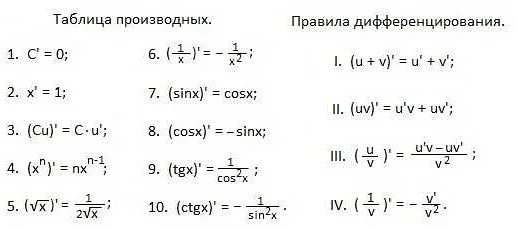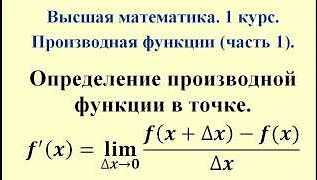Производные в математике как решать

Руководство по производным в математике: что такое производная, как ее находить, основные правила и методы решения задач. Узнайте, как применять производные для определения экстремумов, нахождения касательных и решения задач на оптимизацию.

Производные являются важным инструментом в математике и широко применяются в различных областях науки и техники. Изучение производных позволяет нам анализировать изменение функций и определять их экстремумы, точки перегиба, скорость изменения и другие важные характеристики.

Однако, решение задач на производные может быть сложным и вызывать затруднения у многих студентов. Чтобы эффективно решать такие задачи, необходимо иметь хорошее понимание основных понятий и правил дифференцирования.

Важно отметить, что успех в решении задач с производными зависит от умения увидеть связь между математическими понятиями и реальными ситуациями. Поэтому важно тренировать свою интуицию и умение анализировать проблему, прежде чем приступать к математическим вычислениям.

«Успех в решении задач с производными требует не только знание математических формул и правил, но и умение их применять в реальных ситуациях.»

Кроме того, решение задач на производные требует от студента тщательной работы с формулами и алгебраическими выражениями, умения преобразовывать их и находить общие закономерности. Умение правильно использовать свойства производных и знание различных методов дифференцирования также являются неотъемлемой частью успешного решения задач.

В данной статье мы рассмотрим несколько основных принципов и подходов к решению задач на производные, которые помогут вам стать более уверенным в этой области математики. Мы познакомимся с методами дифференцирования основных элементарных функций и различными способами нахождения производных сложных функций. Также мы рассмотрим примеры задач и их решений, которые помогут вам лучше понять применение производных в реальных задачах.

Что такое производная

Математически производная функции f(x) в точке x называется пределом отношения приращения функции Δf(x) к приращению аргумента Δx, когда Δx стремится к нулю:

f'(x) = lim(Δf(x)/Δx), где Δx → 0

Производная функции показывает, насколько быстро значение функции меняется в данной точке. Если производная положительна, то функция возрастает в этой точке. Если производная отрицательна, то функция убывает. Если производная равна нулю, то функция имеет экстремум (максимум или минимум).

Видео по теме:

Зачем нужна производная

Производная функции в конкретной точке может быть использована для решения различных задач. Например, она может помочь найти экстремальные значения функции, то есть точки минимума и максимума. Также производная позволяет определить, в какую сторону меняется функция: возрастает или убывает.

Знание производной также необходимо при решении задач на определение тангенса угла наклона касательной к графику функции в заданной точке. Это позволяет лучше понять поведение функции и ее особенности в выбранной точке.

Производная также находит применение в физике, экономике, биологии и других науках. Она используется для моделирования и анализа различных процессов, таких как рост популяции, изменение температуры или скорость движения тела.

В общем случае, производная является мощным инструментом, который помогает понять, как одна величина зависит от другой и как они взаимодействуют между собой. Поэтому понимание производной и ее применение в решении задач является важной составляющей математического образования и научных исследований.

Основные правила дифференцирования

Основные правила дифференцирования позволяют находить производную функции, используя простые правила и свойства. В таблице приведены основные правила дифференцирования:

№ПравилоПроизводная

1	Линейность	$(cf)’=cf’$
2	Сумма и разность	$(f+g)’=f’+g’$
3	Произведение	$(f \cdot g)’=f’ \cdot g + f \cdot g’$
4	Частное	$\left(\frac{f}{g} ight)’=\frac{f’ \cdot g — f \cdot g’}{g^2}$
5	Цепное правило	$\left(f(g(x)) ight)’=f'(g(x)) \cdot g'(x)$
6	Степенное правило	$(x^n)’=nx^{n-1}$
7	Экспоненциальная функция	$(e^x)’=e^x$
8	Логарифмическая функция	$(\ln{x})’=\frac{1}{x}$
9	Тригонометрические функции	$(\sin{x})’=\cos{x}$ $(\cos{x})’=-\sin{x}$ $(\tan{x})’=\sec^2{x}$

Знание этих основных правил дифференцирования помогает эффективно решать задачи с производными и легко находить производные сложных функций. Основные правила дифференцирования являются основой для дальнейшего изучения математического анализа и его приложений.

Правило сложения и вычитания

Правило сложения и вычитания гласит, что если у нас есть две функции, то производная суммы/разности этих функций равна сумме/разности производных этих функций.

Математически это можно записать следующим образом:

Правило сложения: Если f(x) и g(x) — две функции, то производная их суммы f(x) + g(x) равна сумме производных этих функций: (f(x) + g(x))’ = f'(x) + g'(x).

Правило вычитания: Если f(x) и g(x) — две функции, то производная их разности f(x) — g(x) равна разности производных этих функций: (f(x) — g(x))’ = f'(x) — g'(x).

Правило сложения и вычитания позволяет упростить выражения и сделать процесс нахождения производных более эффективным. Оно широко используется в различных областях математики и физики.

Это правило полезно при решении задач, где необходимо находить производные сложных выражений, включающих суммы и разности функций. Оно помогает применять другие правила производных и упрощать выражения для дальнейшего анализа.

Правило произведения

Правило произведения позволяет находить производную произведения двух функций. Если даны две функции f(x) и g(x), то производная их произведения f(x)g(x) вычисляется по следующей формуле:

(f(x)g(x))’ = f'(x)g(x) + f(x)g'(x)

То есть производная произведения двух функций равна произведению производной первой функции на вторую функцию и произведению первой функции на производную второй функции.

Это правило очень полезно при решении задач, связанных с нахождением производных сложных функций и функций, представленных в виде произведения.

Важно знать и уметь применять правило произведения при решении задач с производными в математике, так как оно позволяет упростить вычисления и получить более точные результаты.

Правило деления

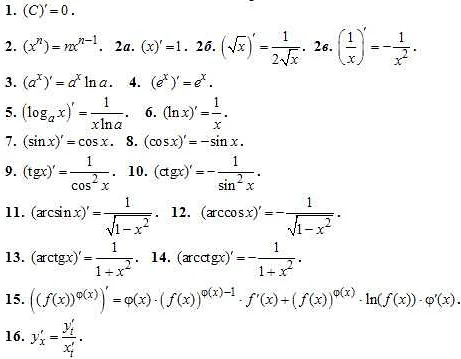
В математике существует правило деления, которое позволяет найти производную отношения двух функций. Это правило также часто называют правилом производной отношения.

Пусть у нас есть две функции: f(x) и g(x). Их отношение обозначается как h(x) = f(x) / g(x).

Формула для нахождения производной отношения функций выглядит следующим образом:

h'(x) = (f'(x) * g(x) — f(x) * g'(x)) / (g(x))^2

где f'(x) и g'(x) обозначают производные функций f(x) и g(x) соответственно.

Это правило особенно полезно при решении задач, связанных с дробными выражениями и долевыми функциями. Оно позволяет найти производную и определить, как меняется отношение двух функций при изменении аргумента.

Пример использования правила деления:

Пусть у нас есть функция f(x) = x^2 и функция g(x) = x. Их отношение будет h(x) = x^2 / x = x.

Применяя правило деления, мы получим:

h'(x) = (2x * x — x^2 * 1) / (x)^2 = (2x^2 — x^2) / x^2 = x / x = 1

Таким образом, производная отношения функций f(x) = x^2 и g(x) = x равна константе 1.

Правило цепной дроби

Правило цепной дроби формулируется следующим образом. Пусть задана функция F(x) = f(g(x)), где f(x) и g(x) — некоторые функции, производные которых известны. Тогда производная функции F(x) может быть найдена по следующему правилу:

Если F(x) = f(g(x))То F'(x) = f'(g(x)) * g'(x)

Это правило основано на том, что при дифференцировании сложной функции с помощью цепного правила, производная внешней функции умножается на производную внутренней функции. Таким образом, правило цепной дроби позволяет разбить сложную функцию на несколько более простых функций и вычислить их производные отдельно.

Применение правила цепной дроби может значительно упростить процесс вычисления производных сложных функций. Оно позволяет снизить задачу нахождения производной сложной функции до задачи нахождения производных составляющих функций.

Например, рассмотрим функцию F(x) = (x^2 + 1)^3. С помощью правила цепной дроби можно разложить эту функцию на две составляющие функции: f(x) = x^3 и g(x) = x^2 + 1. Затем можно вычислить их производные: f'(x) = 3x^2 и g'(x) = 2x. И, наконец, применить правило цепной дроби: F'(x) = f'(g(x)) * g'(x) = 3(x^2 + 1)^2 * 2x.

Таким образом, правило цепной дроби является важным инструментом при решении задач с производными в математике. Оно позволяет эффективно вычислять производные сложных функций, разбивая их на более простые составляющие функции и применяя уже известные производные.

Примеры решения задач с производными

Пример 1:

Найдем производную функции f(x) = 3x^2 + 2x — 1.

Решение:

Используя правила дифференцирования, найдем производную каждого слагаемого:

f'(x) = (3x^2)’ + (2x)’ — (1)’

Получим:

f'(x) = 6x + 2 — 0 = 6x + 2.

Пример 2:

Найдем касательную к графику функции f(x) = x^3 — 4x + 2 в точке x = 2.

Решение:

Для этого найдем производную функции f(x) и подставим значение x = 2:

f'(x) = (x^3 — 4x + 2)’

Получим:

f'(x) = 3x^2 — 4.

Теперь найдем значение производной в точке x = 2:

f'(2) = 3(2)^2 — 4 = 3(4) — 4 = 12 — 4 = 8.

Таким образом, касательная к графику функции в точке x = 2 имеет угловой коэффициент 8.

Пример 3:

Найдем точку экстремума функции f(x) = x^2 + 3x + 1.

Решение:

Для нахождения точки экстремума исследуем производную функции:

f'(x) = (x^2 + 3x + 1)’

Получим:

f'(x) = 2x + 3.

Точка экстремума находится в той точке, где производная равна нулю:

2x + 3 = 0

2x = -3

x = -3/2.

Таким образом, точка экстремума функции f(x) = x^2 + 3x + 1 находится при x = -3/2.

Примеры, приведенные выше, демонстрируют применение производных для решения различных задач в математике. Они показывают, как производные могут быть использованы для нахождения значений функций, касательных и точек экстремума.

Задача на нахождение экстремума функции

Одна из важных задач в математике связана с нахождением экстремумов функций. Экстремумом функции называется точка, где функция достигает максимального или минимального значения.

Для решения задачи на нахождение экстремума функции необходимо найти производную функции и найти ее корни. Корни производной функции являются точками, где функция имеет экстремумы.

Для этого необходимо выполнить следующие шаги:

1. Найти производную функции.
2. Решить уравнение производной, чтобы найти корни.
3. Проверить значения функции в найденных корнях производной: если значение функции в корне производной меньше (больше) нуля, то в данной точке функция имеет локальный минимум (максимум).

Таким образом, решая задачу на нахождение экстремума функции, необходимо найти производную, найти корни производной и определить тип экстремума в каждой из найденных точек.

Решение данной задачи позволяет определить точки, где функция достигает своих наибольших и наименьших значений. Это может быть полезно во многих областях, таких как физика, экономика, статистика и другие, где требуется определить оптимальные значения функций.

Задача на нахождение скорости изменения

Рассмотрим пример задачи на нахождение скорости изменения. Пусть у нас есть автомобиль, движущийся по прямой линии. Мы знаем, что его положение в момент времени t описывается функцией s(t), где s — функция, а t — время. Нам требуется найти скорость изменения положения автомобиля в определенный момент времени.

Для решения этой задачи мы можем воспользоваться производной функции s(t). Производная функции показывает, как быстро меняется значение функции в каждой точке. В данном случае, производная функции s(t) будет являться скоростью изменения положения автомобиля в момент времени t.

Формально, чтобы найти скорость изменения положения автомобиля в момент времени t, мы должны найти производную функции s(t) и подставить значение t в полученное выражение.

Пример решения задачи:

1. Найти производную функции s(t).
2. Подставить значение t в полученную производную функцию.
3. Получить значение скорости изменения положения автомобиля в момент времени t.

Таким образом, решение задач на нахождение скорости изменения требует использования производной функции. Оно позволяет определить скорость изменения в каждой точке и применить полученные знания на практике.

Вопрос-ответ:

Какие методы можно использовать для решения задач с производными?

Для решения задач с производными можно использовать различные методы, такие как метод дифференцирования, метод поиска экстремума, методы интегрирования и так далее. Выбор метода зависит от конкретной задачи и ее условий.

Какие практические примеры можно привести, чтобы продемонстрировать эффективное решение задач с производными?

Один из практических примеров эффективного решения задачи с производными может быть нахождение максимальной площади прямоугольника с фиксированным периметром. В данном случае, используя производные, можно найти размеры прямоугольника, при которых его площадь будет максимальной.

Какие навыки необходимы для эффективного решения задач с производными?

Для эффективного решения задач с производными необходимо иметь хорошее понимание основных понятий дифференциального исчисления, умение применять правила дифференцирования и интегрирования, а также умение анализировать и формулировать математические модели на основе предоставленной информации.

Как можно улучшить свои навыки в решении задач с производными?

Для улучшения навыков в решении задач с производными рекомендуется активное практикование, решение разнообразных задач разной сложности, а также изучение дополнительной литературы и онлайн-курсов по математике. Также полезно работать над пониманием основных понятий и правил дифференциального исчисления.