Пропорции 6 класс математика как решать задачи

Узнайте, как решать задачи по пропорциям в математике для 6 класса. Изучите основные правила и примеры решения задач на пропорции.

Работа с пропорциями – одна из основных тем в курсе математики для учеников 6 класса. Решение задач по пропорциям помогает развивать логическое мышление, аналитические навыки и умение применять математические знания на практике. В этой статье мы рассмотрим основные приемы решения задач по пропорциям и представим несколько примеров, которые помогут вам лучше понять эту тему.

Пропорция – это равенство двух отношений. В задачах по пропорциям встречаются различные величины: длина, ширина, вес, время и другие. Чтобы решить задачу, необходимо установить пропорциональность между этими величинами и найти неизвестное значение.

Один из основных приемов решения задач по пропорциям – использование пропорций и их свойств. Например, если задача требует найти длину отрезка, который делит другой отрезок в заданном отношении, можно воспользоваться свойством пропорции: «произведение средних членов равно произведению крайних». Такой прием позволяет легко решить подобные задачи.

Пример: Велосипедист проехал 40 км за 2 часа, а второй велосипедист проехал этот же путь за 3 часа. С какой скоростью двигался второй велосипедист?

Если первый велосипедист проехал 40 км за 2 часа, то его скорость равна 40/2 = 20 км/ч. Скорость второго велосипедиста можно найти, используя пропорцию: 40/2 = x/3. Умножив средние члены (2 и x) и крайние члены (40 и 3), получим уравнение 2x = 40 * 3. Решив это уравнение, найдем, что x = 60. Значит, второй велосипедист двигался со скоростью 60 км/ч.

Что такое пропорции в математике?

Пропорция состоит из четырех чисел или величин, разделенных на две пары. Первая пара называется первым отношением, а вторая — вторым отношением. Пропорция записывается с помощью знака равенства или двоеточия.

Пропорция может быть представлена в виде уравнения:

a : b = c : d

где a и c — числа или величины из первого отношения, а b и d — числа или величины из второго отношения.

Когда пропорция верна, то отношение между числами или величинами в первой паре равно отношению между числами или величинами во второй паре. Это позволяет использовать пропорции для решения различных задач, как нахождение неизвестной величины, зная другие значения.

Важно понимать, что пропорции могут быть применены в различных областях математики, физики, экономики и других наук, а также в повседневной жизни.

Видео по теме:

Определение и примеры

Пропорция может быть записана следующим образом:

• а : b = c : d
• а : b = c = d

Или с использованием знаков равенства:

• а/b = c/d
• а/b = c = d

Пропорция позволяет решать различные задачи, связанные с пропорциональными отношениями. Например, если известны три числа в пропорции, можно найти четвертое число, используя простую формулу «перемножение средних равно произведению крайних».

Вот примеры задач, которые можно решить с помощью пропорций:

1. Если 5 яблок стоят 60 рублей, сколько стоят 8 яблок?
2. За 4 часа рабочего времени рабочий произвел 120 деталей. Сколько деталей он произведет за 8 часов?
3. Если 3 кг яблок стоят 150 рублей, сколько стоит 1 кг яблок?

Основные приемы решения задач по пропорциям

Решение задач по пропорциям в 6 классе математики основывается на применении нескольких основных приемов.

1. Определение известных величин и неизвестной величины. В задаче обычно даны две пары связанных величин, и нужно найти значение одной из них.
2. Построение пропорции. После определения известных величин и неизвестной величины, можно построить пропорцию, сравнивая соответствующие величины в двух парах.
3. Решение пропорции. Для решения пропорции можно использовать метод перекрестного умножения или метод сокращения, в зависимости от задачи.
4. Проверка ответа. После решения пропорции, следует проверить полученный ответ путем подстановки найденного значения в исходное уравнение и сравнения результатов.

Применение этих приемов позволяет эффективно решать задачи по пропорциям в 6 классе математики. Важно помнить, что для достижения правильного результата необходимо внимательно анализировать задачу и последовательно выполнять каждый шаг решения.

Вопрос-ответ:

Какие основные приемы использовать при решении задач по пропорциям в 6 классе?

Основные приемы при решении задач по пропорциям в 6 классе включают нахождение пропорциональных отношений, составление пропорций и использование правила трех, а также применение метода перевода в одни и те же единицы измерения.

Можете привести пример задачи по пропорциям в 6 классе и показать, как ее решить?

Конечно! Вот пример задачи: «Если 3 кг яблок стоят 150 рублей, сколько стоит 6 кг яблок?». Для решения этой задачи нужно составить пропорцию: 3 кг / 150 рублей = 6 кг / х рублей. Затем, используя правило трех, мы можем найти значение х: 3 кг * х рублей = 150 рублей * 6 кг. Решая это уравнение, получаем, что х = 300 рублей. Таким образом, 6 кг яблок стоят 300 рублей.

Как перевести значения из одних единиц измерения в другие при решении задач по пропорциям в 6 классе?

Если в задаче значения даны в разных единицах измерения, их нужно перевести в одни и те же единицы перед составлением пропорции. Для этого можно использовать соотношение между различными единицами измерения. Например, если в задаче даны значения в килограммах и граммах, то 1 кг = 1000 г. С помощью этого соотношения мы можем перевести значения из граммов в килограммы или наоборот.

Как найти пропорциональные отношения при решении задач по пропорциям в 6 классе?

Для нахождения пропорциональных отношений нужно сравнить два набора чисел или величин и определить, являются ли они пропорциональными. Пропорция состоит из четырех чисел, два из которых составляют первое отношение, а два других — второе отношение. Если отношение первых чисел равно отношению вторых чисел, то набор чисел является пропорциональным.

Как использовать правило трех при решении задач по пропорциям в 6 классе?

Правило трех используется для нахождения неизвестного значения в пропорции. Для этого нужно умножить средние члены (второе и третье число) и разделить полученное произведение на первый член. Например, если пропорция имеет вид: a / b = c / d, то можно найти значение неизвестного числа а, умножив b на c и разделив полученное произведение на d.

Метод подобных треугольников

Для применения метода подобных треугольников необходимо знать следующие свойства:

1. Подобные треугольники имеют равные соотношения сторон.
2. Подобные треугольники имеют равные соотношения высот.
3. Подобные треугольники имеют равные соотношения площадей.

Для решения задач по пропорциям с использованием метода подобных треугольников необходимо:

1. Найти подобные треугольники в задаче.
2. Установить соотношение между сторонами или высотами подобных треугольников.
3. Решить пропорцию для нахождения неизвестной величины.

Пример решения задачи с использованием метода подобных треугольников:

Задача: В треугольнике ABC проведена высота AD. Найти отношение площадей треугольников ABC и ADB, если AB = 8 см, AD = 6 см.

Решение: Треугольники ABC и ADB являются подобными, так как у них равны углы при вершине A (по свойству подобных треугольников). Поэтому можно установить соотношение:

AB/AD = BC/BD

Подставив известные значения, получим:

8/6 = BC/BD

Решим пропорцию и найдем значение BD:

8/6 = BC/BD

8BD = 6BC

BD = 6BC/8

BD = 3BC/4

Таким образом, отношение площадей треугольников ABC и ADB равно 3/4.

Метод подобных треугольников является эффективным инструментом для решения задач по пропорциям в 6 классе математики. Он позволяет использовать свойства подобных треугольников для нахождения неизвестных величин и установления соотношений между ними.

Метод пересечения произведений

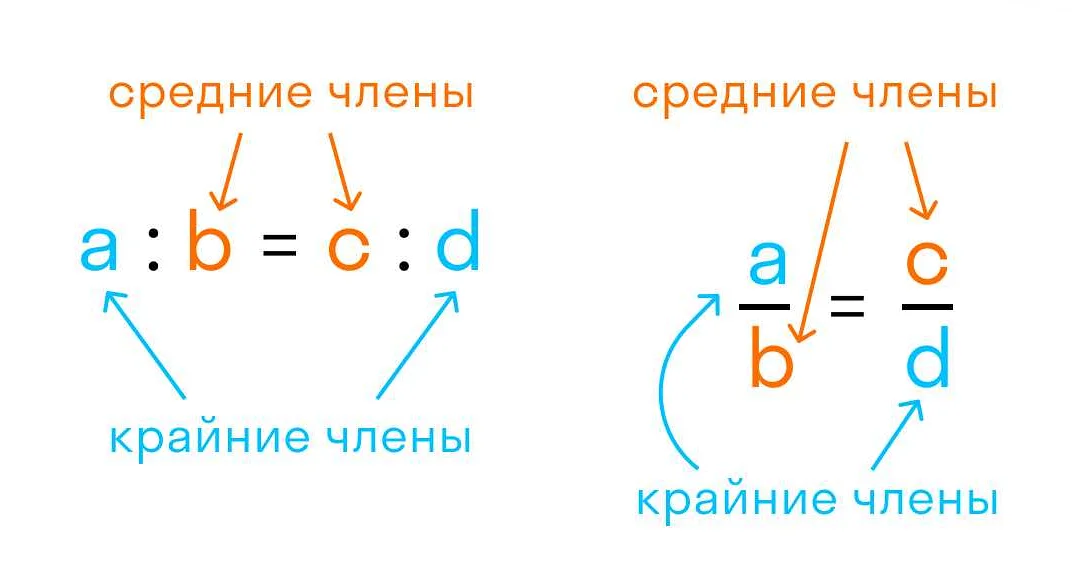
Для применения метода пересечения произведений необходимо знать, что в пропорции отношение двух пар чисел всегда равно. Например, если имеется пропорция a:b = c:d, то можно записать уравнение a/b = c/d. Это уравнение называется пропорцией.

Для решения задачи с использованием метода пересечения произведений нужно знать три из четырех значений в пропорции. Неизвестное значение обозначается буквой, например, х. Затем используя свойство равенства пропорций, можно записать уравнение и решить его.

Примером задачи, которую можно решить с помощью метода пересечения произведений, может быть следующее: «Вася прошел 2 км за 30 минут. Сколько времени ему потребуется, чтобы пройти 4 км?». В данном случае известны значения 2 км и 30 минут, а нужно найти неизвестное значение времени для пройденной дистанции в 4 км.

Для решения этой задачи можно построить пропорцию, используя известные значения 2 км и 30 минут, а также неизвестное значение времени х и пройденную дистанцию 4 км. После записи пропорции a/b = c/d и подстановки известных значений, получим уравнение 2/30 = 4/x. Затем можно перейти к пересечению произведений и решить уравнение, чтобы найти значение x.

Таким образом, метод пересечения произведений является эффективным инструментом для решения задач по пропорциям в 6 классе математики. Он позволяет легко находить неизвестные значения в пропорциональных задачах и развивает навыки работы с пропорциональными отношениями.

Метод средних пропорционалов

Для решения задач с использованием метода средних пропорционалов необходимо следовать следующим шагам:

1. Сформулировать задачу и выразить ее в виде пропорции.
2. Расположить известные значения в пропорции.
3. Найти неизвестное значение, используя свойство пропорции.
4. Проверить полученный результат и сделать вывод.

Рассмотрим пример использования метода средних пропорционалов:

Если 5 мешков картошки стоят 500 рублей, сколько стоит 10 мешков картошки?

Решение:

1. Сформулируем задачу в виде пропорции: 5 мешков картошки — 500 рублей, 10 мешков картошки — ? рублей.
2. Расположим известные значения в пропорции: 5/500 = 10/х.
3. Найдем значение неизвестной величины, умножив крайние члены и средние члены пропорции: 5 * х = 500 * 10.
4. Решим полученное уравнение: х = 5000 / 5 = 1000.
5. Проверим полученный результат: 5/500 = 10/1000.

Таким образом, 10 мешков картошки стоят 1000 рублей.

Метод средних пропорционалов является универсальным и применимым при решении различных задач по пропорциям в 6 классе математики.

Как решать задачи с пропорциями в 6 классе

Для решения задач с пропорциями в 6 классе следует использовать следующие приемы:

1. Нахождение неизвестного члена пропорции. Если известны три величины из пропорции, нужно найти четвертую. Для этого можно использовать правило трех пропорций: значение неизвестного члена равно произведению значений известных членов, деленному на оставшийся известный член.
2. Составление пропорций из условия задачи. Иногда необходимо составить пропорцию самостоятельно, используя условие задачи. Для этого обратите внимание на соотношения между различными величинами и складывайте их в пропорцию.
3. Решение пропорции. После составления пропорции нужно решить ее, чтобы найти значение неизвестного члена. Для этого можно использовать метод перекрестного умножения: произведение значений членов на одной стороне пропорции равно произведению значений членов на другой стороне.

Пропорции могут быть применены для решения различных задач, таких как расчеты в процентах, сравнение величин и нахождение неизвестных значений. Понимание основных приемов решения задач с пропорциями поможет учащимся успешно справляться с математическими заданиями в 6 классе.

Важно помнить, что при решении задач с пропорциями необходимо внимательно читать условие, правильно составлять и решать пропорцию, а также проверять полученный ответ на соответствие условию задачи.

Примеры задач и их решения

Рассмотрим несколько примеров задач по пропорциям и их решений:

ЗадачаРешение

Если 4 яблока стоят 60 рублей, сколько стоят 6 яблок?	Составим пропорцию: 4 яблока / 60 рублей = 6 яблок / х рублей. Решая пропорцию, найдем значение х: х = (6 * 60) / 4 = 90 рублей. Значит, 6 яблок стоят 90 рублей.
Если 5 мешков картошки весят 40 кг, сколько будет весить 8 мешков картошки?	Составим пропорцию: 5 мешков / 40 кг = 8 мешков / х кг. Решая пропорцию, найдем значение х: х = (8 * 40) / 5 = 64 кг. Значит, 8 мешков картошки будут весить 64 кг.
Если 3 работника выполняют задачу за 5 дней, сколько времени потребуется 6 работникам для выполнения той же задачи?	Составим пропорцию: 3 работника / 5 дней = 6 работников / х дней. Решая пропорцию, найдем значение х: х = (6 * 5) / 3 = 10 дней. Значит, 6 работников потребуется 10 дней для выполнения задачи.

При решении задач по пропорциям важно понимать, как составить пропорцию и какие величины сравниваются. Также необходимо следить за единицами измерения и корректно переводить их, если это требуется.

Практические советы для успешного решения

Решение задач по пропорциям в 6 классе математики может показаться сложным, но с помощью следующих советов вы сможете успешно справиться с ними:

1. Внимательно прочитайте условие задачи и выделите ключевую информацию. Она поможет вам правильно сформулировать пропорцию и найти неизвестное значение.

2. Воспользуйтесь принципом равенства долей: если две доли пропорции равны, то и их отношения тоже равны. Это позволяет вам составить уравнение и найти неизвестное значение.

3. Используйте метод перекрестного умножения, чтобы решить пропорцию. Умножьте числа в одной доле и приравняйте их к произведению чисел в другой доле. Затем найдите значение неизвестной величины.

4. Обратите внимание на единицы измерения в задаче. Возможно, вам придется конвертировать одну единицу в другую, чтобы сравнить две величины.

5. Проверьте ваше решение, подставив найденное значение в исходную пропорцию. Оно должно удовлетворять условию задачи.

6. Если вы столкнулись с трудностями, не стесняйтесь обратиться к учителю или использовать дополнительные материалы для практики. Постепенно вы освоите этот навык и сможете решать задачи по пропорциям с легкостью.

Применение пропорций в реальной жизни

Одним из примеров применения пропорций является вычисление расстояния на карте. Если на карте масштаб указан, то с помощью пропорции можно определить фактическое расстояние между двумя точками на местности. Например, если масштаб карты составляет 1 см = 100 м, и вы измерили расстояние между двумя точками на карте и получили 4 см, то фактическое расстояние будет равно 400 м.

Другой пример применения пропорций — это расчет времени. Например, если вы знаете, что вы пешком идете со скоростью 5 км/ч, а расстояние, которое вы должны пройти, составляет 20 км, то с помощью пропорции можно определить, сколько времени вам потребуется для этого. При пропорции 5 км — 1 час, 20 км — x часов, можно решить уравнение и найти значение x.

Пропорции также используются для решения задач в экономике. Например, при расчете стоимости товара по его весу или объему. Если вы знаете стоимость 1 кг товара и его вес, вы можете легко вычислить общую стоимость.

Таким образом, пропорции — это не только математическая концепция, но и полезный инструмент для решения реальных задач. Они помогают нам лучше понять и использовать соотношения между различными величинами в нашей повседневной жизни.