Что такое пропорция в математике простыми словами
Содержимое
- 1 Что такое пропорция в математике простыми словами
- 1.1 Пропорция в математике: базовое понятие
- 1.2 Составляющие пропорции: числитель и знаменатель
- 1.3 Как определить эквивалентность пропорций?
- 1.4 Различные виды пропорций в математике
- 1.5 Как решать задачи на пропорцию?
- 1.6 Применение пропорций в реальной жизни
- 1.7 Вопрос-ответ:
- 1.8 Полезные свойства и примеры пропорций
- 1.9 Видео по теме:
Пропорция в математике – это отношение или соотношение между двумя или более числами. В данной статье мы разберем, как понять и использовать пропорцию в простых и понятных словах. Узнайте, как применять пропорцию в решении математических задач и понять ее значение в повседневной жизни.
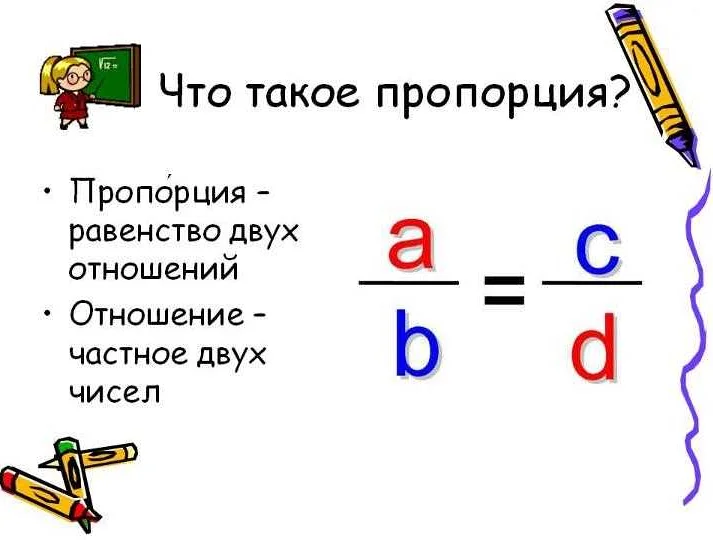
Пропорция – это математическое понятие, которое используется для сравнения двух или более величин. Она помогает нам определить, насколько одна величина соотносится с другой. Пропорции используются во многих областях науки, экономики и повседневной жизни.
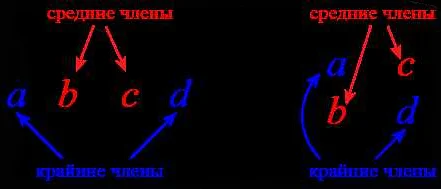
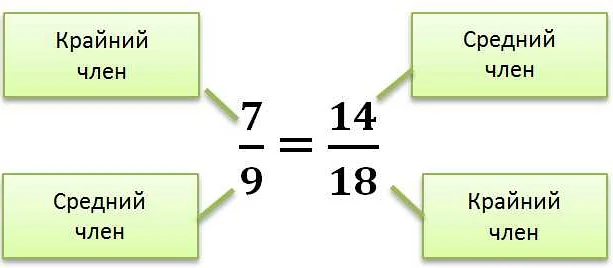
Пропорция состоит из четырех чисел или выражений, разделенных знаком равенства или двоеточием. Четыре числа образуют две пары, и каждая пара имеет свою особенность. Если пропорция выполняется, то одна пара чисел пропорциональна другой паре. Это означает, что соотношение между числами в каждой паре одинаково.
Например, если у нас есть пропорция 2:4 = 3:6, это означает, что отношение между числами 2 и 4 такое же, как отношение между числами 3 и 6. В данном случае, оба отношения равны 1:2.
Пропорции могут быть полезны при решении различных задач, таких как нахождение неизвестного значения в пропорции или сравнение двух наборов данных. Они позволяют нам анализировать и понимать соотношения между различными числами и выражениями.
Пропорция в математике: базовое понятие

Пропорция состоит из четырех чисел или величин, которые образуют две пары: числитель и знаменатель для первой величины, и числитель и знаменатель для второй величины. Обычно пропорцию записывают в виде:
a:b = c:d
где a и b — числители и знаменатели для первой величины, а c и d — числители и знаменатели для второй величины.
Пропорция может быть прямой или обратной. В прямой пропорции, если одна величина увеличивается, то и другая увеличивается пропорционально. В обратной пропорции, если одна величина увеличивается, то другая уменьшается пропорционально.
Пропорции широко используются в разных областях, например, в финансах, науке и инженерии, для решения различных задач и определения соотношений между величинами.
Составляющие пропорции: числитель и знаменатель
Числитель — это число, которое находится сверху дроби. Он определяет количество единиц или частей, которые мы рассматриваем. Например, если мы говорим о пропорции между количеством мальчиков и девочек в классе, числитель будет представлять количество мальчиков.
Знаменатель — это число, которое находится внизу дроби. Он определяет размерность или единицу измерения, в которой мы рассматриваем числитель. Например, если мы говорим о пропорции между количеством мальчиков и девочек в классе, знаменатель будет представлять количество девочек.
Чтобы построить пропорцию, мы сравниваем два отношения, где числитель одного отношения равен знаменателю другого отношения. Например, если у нас есть пропорция между количеством мальчиков и девочек в двух классах, мы можем записать ее следующим образом:
Мальчики в классе А / Девочки в классе А = Мальчики в классе В / Девочки в классе В
Таким образом, числитель и знаменатель играют важную роль в определении отношений и построении пропорций в математике.
Как определить эквивалентность пропорций?
Для определения эквивалентности пропорций необходимо сравнить их значения и установить, равны ли они друг другу. Эквивалентные пропорции имеют одинаковое отношение между своими частями.
Для этого можно воспользоваться методом перекрестного умножения или сокращения.
Метод перекрестного умножения заключается в следующем: если в двух пропорциях отношения между числами равны, то произведение крайних членов будет равно произведению средних членов. Если эти произведения равны, то пропорции эквивалентны.
Метод сокращения заключается в сокращении или упрощении пропорции до наименьших возможных значений. Если после сокращения получатся одинаковые результаты, то пропорции эквивалентны.
Например, рассмотрим следующие пропорции:
Пропорция 1: 2:4 = 3:6
Пропорция 2: 5:10 = 2:4
Применяя метод перекрестного умножения, мы получаем:
2 * 6 = 4 * 3
12 = 12
Таким образом, пропорции 1 и 2 эквивалентны.
Применяя метод сокращения, мы можем упростить пропорции:
Пропорция 1: 2:4 = 1:2
Пропорция 2: 5:10 = 1:2
Таким образом, пропорции 1 и 2 также эквивалентны.
Используя эти методы, можно определить, являются ли пропорции эквивалентными или нет.
Различные виды пропорций в математике
В математике существуют различные виды пропорций, которые используются для решения разнообразных задач. Они позволяют находить неизвестные значения, исходя из известных пропорциональных соотношений.
Одним из наиболее простых и широко используемых видов пропорций является пропорция прямой. В этой пропорции отношение между двумя парами чисел остается постоянным. Например, если мы знаем, что 2 часа равны 120 минутам, то можем установить пропорцию:
ЧасыМинуты
| 2 | 120 |
| x | y |
В этой пропорции нам известны значения для первой пары чисел (2 и 120), и мы хотим найти значения для второй пары чисел (x и y). Решая эту пропорцию, мы можем найти, что x равно 4 и y равно 240.
Еще одним видом пропорции является обратная пропорция. В этой пропорции отношение между числами изменяется обратно пропорционально. Например, если мы знаем, что при увеличении скорости автомобиля время, затраченное на преодоление расстояния, уменьшается, то можем установить пропорцию:
Скорость (км/ч)Время (ч)
| 60 | 4 |
| x | y |
В этой пропорции нам известны значения для первой пары чисел (60 и 4), и мы хотим найти значения для второй пары чисел (x и y). Решая эту пропорцию, мы можем найти, что x равно 15 и y равно 0.25.
Также существуют и другие виды пропорций, такие как смешанные пропорции, равномерные пропорции и т.д. Каждый из этих видов пропорций имеет свои особенности и применяется в различных ситуациях.
Как решать задачи на пропорцию?
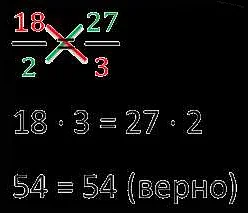
Решение задач на пропорцию в математике может быть достаточно простым, если вы знакомы с основными правилами работы с пропорциями.
Для начала, необходимо определить, что является известными величинами в задаче и что нужно найти. Обычно, в задачах на пропорцию известны две пары величин, связанных между собой пропорциональной зависимостью. Например, величины A и B связаны пропорцией A:B = C:D.
Для решения задачи на пропорцию, необходимо найти значение одной из неизвестных величин. Для этого можно использовать два основных метода: метод равных отношений и метод продуктов.
Метод равных отношений заключается в том, что известное отношение пропорции равно неизвестному отношению пропорции. Например, если известно, что A:B = C:D, и неизвестная величина D, то можно записать равенство A:B = C:D и выразить D через A и B.
Метод продуктов заключается в том, что произведение известных величин равно произведению неизвестных величин. Например, если известно, что A:B = C:D, и неизвестная величина D, то можно записать равенство A*B = C*D и выразить D через A и B.
После того, как вы выразили неизвестную величину через известные, можно произвести вычисления и найти ответ на задачу.
Важно помнить, что при решении задач на пропорцию нужно быть внимательным и аккуратным, чтобы не допустить ошибок в вычислениях и получить правильный результат.
ПримерРешение
| Если 4 литра молока стоят 200 рублей, сколько стоит 6 литров молока? | Известно, что 4 литра молока стоят 200 рублей. Таким образом, соотношение между количеством молока и его стоимостью равно 4:200. Необходимо найти стоимость 6 литров молока. Для этого, используем метод продуктов: 4 * x = 6 * 200, где x — стоимость 6 литров молока. Решив данное уравнение, получим x = 600 рублей. Таким образом, 6 литров молока стоят 600 рублей. |
Применение пропорций в реальной жизни
Одним из примеров применения пропорций является решение задач финансового характера. Например, при планировании бюджета или расчете скидки на товары можно использовать пропорции. Если известна цена одного товара и его количество, а также цена другого товара, то можно найти, сколько нужно денег потратить на второй товар.
Еще одним примером применения пропорций является строительство и архитектура. Здесь пропорции используются для создания гармоничных и эстетически приятных сооружений. Архитекторы и дизайнеры часто используют пропорцию Золотого сечения для создания пропорциональных форм и размеров.
Пропорции также находят применение в медицине. Например, при расчете дозировки лекарств пропорции помогают найти правильное соотношение между количеством лекарства и весом пациента.
Использование пропорций распространено и в других областях, таких как география, экономика, физика и т.д. Они помогают найти правильные соотношения и решить различные задачи, основанные на пропорционных отношениях между величинами.
Таким образом, пропорции являются важным инструментом в решении различных задач в реальной жизни, позволяя нам находить соотношения и сравнивать различные величины.
Вопрос-ответ:
Зачем нужна пропорция в математике?
Пропорция в математике используется для решения задач, связанных с сравнением и сопоставлением двух или более величин. Она позволяет находить неизвестные значения, если известны значения других величин, причем величины должны быть пропорциональны. Это очень полезный инструмент при работе с разными объектами и явлениями, в том числе в финансах, инженерии, физике, геометрии и других областях.
Что значит «пропорционально» в математике?
В математике две или более величины считаются пропорциональными, если они связаны таким образом, что при изменении одной величины другая также изменяется, сохраняя определенное отношение. Это отношение называется коэффициентом пропорциональности. Если две величины пропорциональны, то можно построить пропорцию, которая позволяет находить неизвестные значения при известных. Пропорциональность можно выразить и в виде уравнения, где коэффициент пропорциональности является коэффициентом перед неизвестной величиной.
Как записывается пропорция в математике?
Пропорция в математике записывается в виде отношения двух равносторонних дробей. Обычно используются буквы a, b, c, d для обозначения величин в пропорции. Пропорция записывается в виде a/b = c/d или a:b = c:d. Здесь a и c — это числители, а b и d — это знаменатели. Если известны три из четырех величин, можно использовать пропорцию для нахождения четвертой неизвестной величины.
Как решать задачи на пропорцию в математике?
Для решения задач на пропорцию в математике нужно следовать нескольким шагам. Во-первых, записать известные значения и неизвестные как a/b = c/d или a:b = c:d. Во-вторых, использовать свойство пропорции для нахождения неизвестной величины. Для этого нужно умножить числитель и знаменатель одной дроби на одно и то же число, чтобы получить равные произведения. В-третьих, решить получившееся уравнение и найти значение неизвестной величины. Наконец, проверить полученный результат и ответить на вопрос задачи.
Что такое пропорция?
Пропорция — это математическое соотношение, которое устанавливает равенство двух отношений. В пропорции сравниваются четыре числа, причем отношение первых двух чисел равно отношению вторых двух чисел.
Как определить пропорцию?
Для определения пропорции необходимо сравнить отношения двух пар чисел. Если эти отношения равны, то имеется пропорция. Пропорция можно записать в виде a:b = c:d, где a, b, c и d — числа.
Полезные свойства и примеры пропорций
Одно из полезных свойств пропорций — свойство перестановки местами средних членов. То есть, если пропорция a:b=c:d верна, то также верны пропорции b:a=d:c и c:d=a:b.
Другое полезное свойство — свойство умножения на одно и то же число. Если пропорция a:b=c:d верна, то для любого числа n также верна пропорция na:nb=nc:nd.
Рассмотрим несколько примеров пропорций. Например, для пропорции 2:3=4:6 можно умножить все члены на 2 и получить 4:6=8:12, что также будет верной пропорцией.
Еще один пример — пропорция 3:5=6:10. Заметим, что мы можем переставить местами средние члены и получить пропорцию 5:3=10:6, которая также будет верной.
Пропорции часто используются в решении задач, связанных с пропорциональными зависимостями. Например, если мы знаем, что 2 яблока стоят 10 рублей, то мы можем использовать пропорцию, чтобы выяснить сколько стоят 5 яблок.



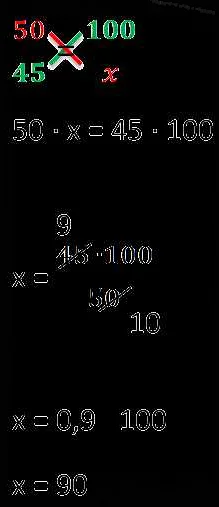

Прекрасная статья, очень понятно и доступно объяснено понятие пропорции в математике! Я всегда путалась в этих сложных формулах, но благодаря вашей статье смогла разобраться. Пропорция — это соотношение между разными величинами, когда они сохраняют одинаковое отношение. Например, если у нас есть две дроби, и их числители и знаменатели также соответствуют друг другу, то это значит, что у нас есть пропорция. Теперь мне понятно, как решать задачи на пропорциональное деление и умножение. Спасибо за ясное объяснение! Жду продолжения статей на эту тему.
Математика всегда казалась мне непонятной и сложной наукой, но статья про пропорцию в математике подарила мне ясность и понимание. Пропорция — это связь между четырьмя числами или величинами, где соотношение между ними остается неизменным. Например, если у нас есть две пары чисел, то мы можем определить, являются ли они пропорциональными, сравнивая их отношения. Важно понимать, что пропорция может быть прямой или обратной. Простыми словами, пропорция помогает нам установить связь между числами и выявить закономерности. Как женщине, мне приятно осознавать, что математика может быть доступной и понятной, благодаря таким простым объяснениям.
Пропорция в математике — это связь между четырьмя числами или выражениями, которая говорит о том, что их отношения равны друг другу. Простыми словами можно сказать, что пропорция — это какое-то равенство, которое соблюдается между числами. Например, если у нас есть две пары чисел, например 2 и 4, 6 и 12, то их отношение равно 2:4=6:12, и мы можем сказать, что эти пары чисел образуют пропорцию. Пропорции могут быть полезными в решении различных задач, например, при сравнении цен на товары или при расчете долей в смеси. Понимание пропорций поможет нам лучше понять связь между числами и использовать её в повседневной жизни.