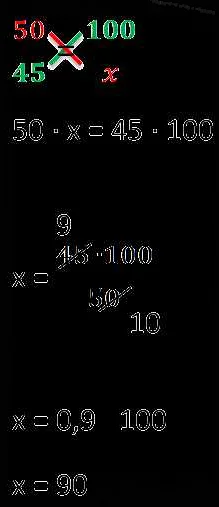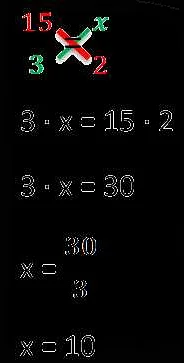Как правильно составить пропорцию в математике: простые шаги и советы

Узнайте, как правильно составить пропорцию в математике и сделать правильное решение задач. Изучайте шаг за шагом пошаговый алгоритм и примеры для понимания. Полезные советы и рекомендации для лучшего понимания темы.

Пропорция – это одно из основных понятий в математике, которое часто используется в различных задачах. Она позволяет сравнивать разные величины и находить неизвестные значения. Но как правильно составить пропорцию и решить задачу?

В этой статье мы расскажем о том, как составлять пропорции и какие правила следует при этом учитывать. Мы предложим несколько примеров задач и покажем, как применять полученные знания на практике. Эта информация будет полезна не только школьникам, но и всем, кто хочет развить свои математические навыки.

Чтобы работать с пропорциями, нужно знать теорию и уметь применять ее на практике. В этой статье мы постарались объяснить все основные моменты и дать понятные примеры. Надеемся, что после прочтения вы сможете сами составлять пропорции и решать задачи без проблем.

Определение пропорции в математике

Пропорция – это математический термин, который означает соотношение между двумя или более размерами. Пропорция может быть выражена как отношение между двумя парными элементами.

Простая пропорция представляет собой равенство двух дробей. Каждый элемент в левой дроби соответствует элементу в правой дроби, подобно тому, как соответствует частям тела каждого отдельного человека его рост и вес.

Составная пропорция – это пропорция, которая содержит более двух пар элементов. Эти пары элементов могут быть скомбинированы так, чтобы получить несколько дробей. Для решения составной пропорции нужно использовать комплексные математические операции, такие как умножение и деление.

Пропорция является важным понятием в математике, физике, экономике и других науках. Знание теории пропорций может использоваться для определения неизвестных значений, совершения сложений и вычитаний, а также большего понимания отношений между различными переменными.

Основные свойства пропорциональности

Пропорциональность — это математическое отношение между двумя переменными, при котором изменение одной переменной приводит к соответствующему изменению другой в соотношении некоторой постоянной величины.

Основными свойствами пропорциональности являются:

• Первое свойство: Если значения одной переменной изменяются в одинаковой пропорции с другой переменной, то эти две переменные пропорциональны. Например, если стоимость 1 кг яблок составляет 100 рублей, то стоимость 2 кг яблок будет равна 200 рублей.
• Второе свойство: Если значение одной переменной увеличивается в m раз, а значение другой переменной увеличивается в n раз, то эти две переменные пропорциональны. Например, если 5 карандашей стоят 12 рублей, то 10 карандашей будут стоить 24 рубля.
• Третье свойство: Если значения двух пар переменных пропорциональны, то они пропорциональны и все 4 переменных. Например, если расстояние между двумя городами равно 500 км за 10 часов, то расстояние 1000 км займет 20 часов.

Основные свойства пропорциональности помогают определить, являются ли две переменные пропорциональными, а также решать уравнения и задачи, связанные с пропорциональностью.

Как составить пропорцию: шаг за шагом

Пропорция — это математическая концепция, которая используется для сравнения двух или более величин. Для правильного составления пропорции необходимо следовать нескольким шагам:

1. Определите, какие величины вы хотите сравнить: пропорция состоит из двух пар величин, которые нужно сравнить друг с другом. Например, вы можете хотеть сравнить количество золота и серебра, которое вы получаете за определенную работу.
2. Определите единицы измерения: чтобы пропорция была правильной, необходимо, чтобы сравниваемые величины имели одинаковые единицы измерения. Например, если вы сравниваете количество золота и серебра, они должны иметь одинаковые единицы измерения, например граммы, унции или килограммы.
3. Расположите величины в правильном порядке: в пропорции первая пара величин обычно описывается как «отношение» (a:b), а вторая пара — как «известные» (c:d). Порядок расположения величин в пропорции должен быть одинаковым: a:b = c:d.
4. Решите пропорцию: чтобы решить пропорцию, умножьте крест-накрест первую и вторую пары величин и сравните результаты. Например, если ваша пропорция имеет вид 2:3 = c:12, вы можете умножить крест-накрест, получив уравнение 2*12=3*c. Затем решите уравнение, чтобы найти значения неизвестных величин.

Составление пропорции — это основа многих различных математических концепций, таких как проценты, доли и пропорциональность. При правильном использовании пропорций вы можете решать сложные задачи с легкостью.

Примеры решения задач на пропорциональность

Пример 1: Если 10 мешков яблок стоят 2500 рублей, то сколько стоят 20 таких мешков?

Решение:

1. Напишем пропорцию: 10/2500 = 20/x
2. Разделим правую и левую части на 10: 1/250 = 2/x
3. Перемножим числа на обеих сторонах уравнения: x = 5000

Ответ: 20 мешков яблок стоят 5000 рублей.

Пример 2: Если 4 рабочих могут выполнить работу за 15 дней, то за сколько дней выполнит такую же работу 3 рабочих?

Решение:

1. Напишем пропорцию: 4/15 = 3/x
2. Разделим правую и левую части на 3: 4/45 = 1/x
3. Перемножим числа на обеих сторонах уравнения: x = 45

Ответ: 3 рабочих выполнят работу за 45 дней.

Пример 3: Если 5 яблок стоят 25 рублей, то сколько стоят 3 яблока?

Решение:

1. Напишем пропорцию: 5/25 = 3/x
2. Разделим правую и левую части на 5: 1/5 = 3/x
3. Перемножим числа на обеих сторонах уравнения: x = 15

Ответ: 3 яблока стоят 15 рублей.

Сводная таблица примеров решения задач на пропорциональностьПримерУсловие задачиРешениеОтвет

1	Если 10 мешков яблок стоят 2500 рублей, то сколько стоят 20 таких мешков?	10/2500 = 20/x; 1/250 = 2/x; x = 5000	20 мешков яблок стоят 5000 рублей
2	Если 4 рабочих могут выполнить работу за 15 дней, то за сколько дней выполнит такую же работу 3 рабочих?	4/15 = 3/x; 4/45 = 1/x; x = 45	3 рабочих выполнят работу за 45 дней
3	Если 5 яблок стоят 25 рублей, то сколько стоят 3 яблока?	5/25 = 3/x; 1/5 = 3/x; x = 15	3 яблока стоят 15 рублей

Как определить пропорциональность графически

Пропорциональность является одним из основных понятий математики, и она может быть определена не только алгебраически, но и графически. Если мы хотим определить, является ли зависимость между двумя величинами пропорциональной, мы можем нарисовать график и проанализировать его.

Если величины пропорциональны, график будет представлять собой прямую линию, которая проходит через начало координат. Следовательно, величины будут иметь одинаковый коэффициент пропорциональности для всех точек на графике. В этом случае, мы можем использовать уравнение прямой для определения этого коэффициента.

Если график не является прямой линией, тогда величины не являются пропорциональными. Мы можем, однако, использовать график для определения того, как зависимость между величинами меняется в зависимости от значения одной из них. Например, если график имеет форму параболы, мы можем определить, что зависимость является квадратичной и количество изменения двух переменных не является одинаковым.

В целом, графическое определение пропорциональности может быть очень полезным инструментом в математике. График может помочь нам понять не только саму пропорциональность, но также и общую зависимость между величинами. Это может использоваться для принятия решений в разных областях, таких как экономика, финансы и наука.

Обратная пропорциональность: определение и примеры

Обратная пропорциональность — это математическое понятие, которое относится к двум переменным, таким образом, что одна переменная увеличивается пропорционально уменьшению другой переменной. Или же, при увеличении одной переменной, другая переменная уменьшается пропорционально.

Примеры обратной пропорции можно найти во многих сферах жизни, например:

• Чем больше людей живут в одной квартире, тем меньше места остается для каждого;
• Чем больше время, потраченное на одну задачу, тем меньше задач можно выполнить за определенный период;
• Чем больше скорость движения, тем меньшее время занимает дистанция, пересекаемая за определенное время.

Математически обратная пропорция может быть записана следующим образом:

y = k / x

где x — первая переменная, y — вторая переменная, а k — постоянное значение, которое не изменяется в ходе измерений.

Если переменные x и y обратно пропорциональны, то k может быть найдено из измерений, выполненных для этих переменных. Значение постоянной фиксируется, когда одна переменная увеличивается в пропорции с уменьшением другой переменной.

Как решать задачи на обратную пропорциональность

Обратная пропорциональность – это свойство, при котором две величины зависят друг от друга так, что при уменьшении одной из них, другая увеличивается. Для решения задач на обратную пропорциональность необходимо знать формулу, по которой она определяется: A * B = C.

Для применения этой формулы необходимо выделить две величины и найти, как они взаимосвязаны. Затем можно рассчитать третью величину. Например, если известно, что человек прошел 10 км за 1 час, то можно найти сколько времени ему понадобится, чтобы пройти 20 км. Для этого нужно использовать формулу обратной пропорциональности: 10 * 1 = 20 * x, где x – время, которое потребуется человеку для прохождения 20 км. Решив эту формулу, мы получим x = 0,5 часа.

Если в задаче даны три величины, то стоит выделить две из них и применить формулу обратной пропорциональности. Например, если известно, что 20 рабочих могут завершить работу за 10 дней, то каково количество дней, которое потребуется 30 рабочим? Для решения этой задачи можно использовать формулу обратной пропорциональности: 20 * 10 = 30 * x, где x – количество дней, которые понадобятся 30 рабочим. Решив эту формулу, мы получим x = 6,67 дней.

Важно помнить, что формула обратной пропорциональности работает только для двух величин, и что она применима только в случае, если величины обратно пропорциональны друг другу. При решении задач на обратную пропорциональность также важно не забывать о выборе правильных единиц измерения и внимательно читать условия задачи.

Чтобы лучше понимать этот материал, стоит решать разнообразные задачи на обратную пропорциональность. Это поможет закрепить знания и научиться справляться с непредвиденными ситуациями в жизни, где необходимо быстро применить математические знания.

Преобразование пропорций для удобства решения задач

Пропорции часто используются в математике для решения различных задач, таких как расчеты количественных характеристик или выявление соотношений между объектами. Однако, иногда пропорции могут быть не очень удобными для решения задач и требуют преобразований.

Для удобства решения задач, пропорции могут быть упрощены путем сокращения общих сомножителей. Например, если имеется пропорция:

a : b = c : d

Ее можно упростить, разделив каждое число на наибольший общий делитель (НОД) двух пар чисел a и b, c и d.

Пропорции также могут быть преобразованы путем изменения расположения чисел внутри них. Например, если имеется пропорция:

a : b = c : d

Ее можно преобразовать, поменяв местами числа b и c:

a : c = b : d

Также пропорции могут быть представлены в виде процентов, что может значительно облегчить их решение. Например, если имеется пропорция:

a : b = c : d

Ее можно представить в виде процентов, разделив числа на их сумму:

• проценты, соответствующие a и c, будут равны (a / (a + b)) х 100% и (c / (c + d)) х 100%, соответственно;
• проценты, соответствующие b и d, будут равны (b / (a + b)) х 100% и (d / (c + d)) х 100%, соответственно.

Кроме того, пропорции могут быть преобразованы в другие формы, такие как уравнения, системы уравнений и т.д., в зависимости от поставленной задачи и используемых методов.

Как проверять правильность составления пропорции

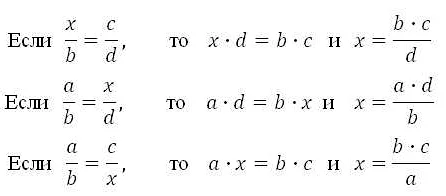
В математике пропорция – это сравнение двух знаменателей и двух числителей. Она часто используется при решении различных задач, связанных с расчетами и построениями. Составление пропорции может быть довольно сложным процессом, поэтому необходимо уметь проверять правильность ее составления.

Первым шагом при проверке пропорции является убеждение в том, что она действительно нужна для решения задачи. Это можно сделать, сравнив знаменатели и числители двух отношений. Если они равны, то пропорция не нужна.

Вторым шагом является проверка правильности написания пропорции. Обычно пропорции записывают в виде «a:b = c:d» или «a/b = c/d». Необходимо убедиться, что числитель a соответствует знаменателю c, и что числитель b соответствует знаменателю d.

Далее необходимо убедиться в правильности составления пропорции. Для этого можно выполнить кросс-умножение. Если при произведении числителей получится то же самое число, что и при произведении знаменателей, то пропорция составлена правильно.

В случае, если кросс-умножение не дает одинаковых результатов, необходимо перепроверить исходные данные и попробовать пересчитать пропорцию. Если ошибка не будет обнаружена, то, скорее всего, в исходных данных была допущена ошибка.

Таким образом, проверка правильности составления пропорции является важным шагом в решении задач, связанных с математическими расчетами. При выполнении этого шага необходимо быть внимательным и тщательным, чтобы избежать ошибок и получить правильный результат.

Применение пропорций в повседневной жизни

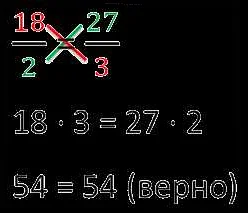
Пропорции являются одним из фундаментальных математических понятий и применяются в повседневной жизни в самых разных сферах.

Например, в строительстве и дизайне пропорции используются для создания гармоничного и эстетичного визуального впечатления. Архитекторы и дизайнеры используют золотое сечение и другие пропорции для распределения пространства и формирования соотношений между объектами.

Пропорции также применяются в кулинарии. При приготовлении блюд, необходимо соблюдать определенные пропорции ингредиентов, чтобы получить нужную текстуру, вкус и аромат блюда.

В финансовой сфере пропорции помогают рассчитать процентные ставки, а в бизнесе — выявить зависимость между различными факторами.

Пропорции также используются в медицине для расчета дозы лекарств и пропорций различных компонентов в медицинских препаратах.

Кроме того, пропорции применяются в географии для вычисления масштаба карты и на карточках метро для отображения стоимости проезда в зависимости от расстояния и количества остановок.

В общем, пропорции являются неотъемлемой частью нашей повседневной жизни и играют важную роль в различных сферах деятельности.

Вопрос-ответ:

Какие пропорциональные отношения бывают в математике?

В математике наиболее распространены три типа пропорциональных отношений: прямая пропорциональность, обратная пропорциональность и компонентная пропорциональность.

Как определить, является ли заданная пропорция прямой или обратной?

Для определения типа пропорции нужно сравнить отношения значений первой и второй величины с отношениями значений третьей и четвертой величины. Если отношения первых двух величин равны отношениям последних двух величин, то пропорция является прямой. Если же отношения первых двух величин обратны отношениям последних двух величин, то пропорция является обратной.

Какую формулу использовать для решения задач на пропорциональные отношения?

Формула для решения задач на пропорциональные отношения имеет вид: первая величина * вторая величина = третья величина * четвертая величина. Эту формулу можно использовать для нахождения любой из четырех величин, если известны остальные три.

Можно ли применять пропорциональные отношения в жизни?

Да, пропорциональные отношения широко применяются в жизни, например, при расчете пропорции ингредиентов для приготовления блюда, вычислении дистанции между городами на карте, определении соотношения площадей участков земли и т. д.

Можно ли решать задачи на пропорциональные отношения без формул?

Да, некоторые задачи на пропорциональные отношения можно решать без использования формул, а только с помощью логических рассуждений. Например, задачу о том, что если четыре рабочих за два часа выполняют работу, то на сколько времени нужно нанять дополнительных два рабочих, чтобы работа была выполнена за один час, можно решать только логически, используя пропорциональность отношений времени и числа рабочих.

Может ли пропорция быть неверной?

Да, пропорция может быть неверной, если сравниваемые величины не имеют между собой прямой или обратной зависимости. Например, если сравнивать величины «вес автомобиля» и «доход владельца», то пропорция будет неверной, так как эти величины не имеют между собой прямой или обратной зависимости.

Как находить неизвестные величины в сложных пропорциях?

Для нахождения неизвестных величин в сложных пропорциях нужно разбить их на простые пропорции и решать каждую из них по отдельности, используя формулу первой величины * вторая величина = третья величина * четвертая величина.

Польза изучения пропорций для математического мышления

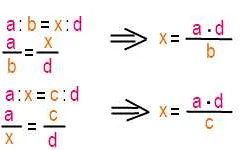
Пропорции – это одно из важных понятий в математике, которое помогает понимать, как связаны различные элементы в задаче. Изучение пропорций не только обогащает математическое мышление, но и помогает в повседневной жизни в решении разных задач. Например, если мы говорим о купле продукта, то мы можем использовать пропорции для вычисления соответствующего количества. Также, пропорции используются в финансах, в строительстве и в других областях.

Изучение пропорций помогает не только решать задачи, но и развивает абстрактное и логическое мышление. При работе с пропорциями требуется анализировать, какие факторы могут влиять на результаты. Чтобы решить задачу с пропорцией, нужно определить соотношение между элементами в ней – это помогает развивать логическое мышление. Кроме того, при изучении пропорций, могут использоваться разные алгоритмы, которые улучшают креативность и способность находить нестандартные решения.

В целом, изучение пропорций развивает многие ценные навыки, необходимые не только в математике, но и в повседневной жизни. Это выработка абстрактного мышления, логического мышления и способности к анализу, аналитическому мышлению, креативности и способности находить нестандартные решения.

Видео по теме: