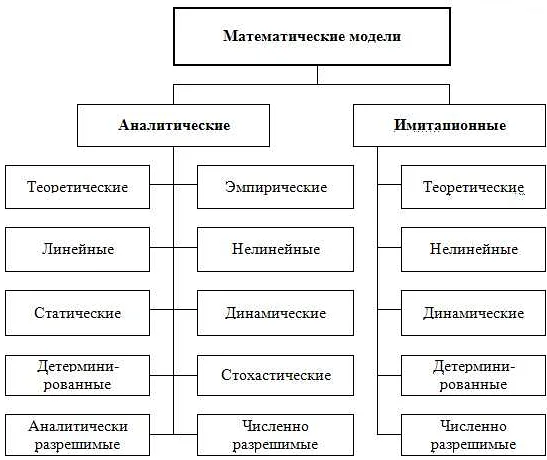
Признаки по которым классифицируются математические модели

Узнайте о признаках, по которым классифицируются математические модели. Отличите статические и динамические модели, линейные и нелинейные, дискретные и непрерывные. Узнайте, как правильно выбирать модель для конкретной задачи.

В научных и инженерных исследованиях математические модели являются неотъемлемой частью процесса понимания и анализа сложных явлений. Они помогают упростить реальный мир, абстрагируясь от его сложности и учитывая только те аспекты, которые нас интересуют. Однако для эффективного использования математических моделей необходимо понимать их основные признаки и критерии классификации.

Основным признаком математической модели является ее структура. Модели могут быть линейными или нелинейными, дискретными или непрерывными, стохастическими или детерминированными. Линейные модели представляют собой линейные соотношения между переменными, тогда как нелинейные модели описывают нелинейные зависимости. Дискретные модели имеют конечное или счетное число состояний или переменных, в то время как непрерывные модели описывают непрерывные процессы. Стохастические модели учитывают случайность, а детерминированные модели представляют собой строго определенные взаимосвязи.

Критерии классификации математических моделей включают в себя адекватность, точность, простоту и объяснительную способность. Адекватность математической модели означает, что она должна корректно описывать и предсказывать реальное явление. Точность модели связана с ее способностью предсказывать значения переменных с высокой степенью точности. Простота модели предполагает минимальное количество переменных и параметров для описания явления. Объяснительная способность модели заключается в ее способности объяснить причины и механизмы, лежащие в основе явления.

Важно отметить, что классификация математических моделей может быть достаточно сложной задачей, так как модели могут иметь различные комбинации признаков и критериев. Кроме того, выбор математической модели должен быть обоснован и основываться на реальных данных и предположениях. Неправильный выбор модели может привести к неверным результатам и неверным выводам.

В заключение, понимание основных признаков и критериев классификации математических моделей является важным для создания и использования эффективных и адекватных моделей. Это позволяет ученым и инженерам более глубоко понять и объяснить сложные явления, а также предсказывать их поведение в различных условиях.

Определение математической модели и ее роль в науке

Роль математической модели в науке является важной и неотъемлемой. Она позволяет ученым формализовывать реальные явления, выражать их в виде уравнений и символов, а затем анализировать их с помощью методов математики.

Математические модели могут быть использованы в различных областях научного исследования, таких как физика, химия, биология, экономика и т.д. Они позволяют предсказывать поведение системы в различных условиях, проводить эксперименты в виртуальной среде, оптимизировать процессы и принимать обоснованные решения.

Преимущества математических моделей включают точность, возможность проведения экспериментов в условиях, которые в реальности недоступны, и возможность анализа сложных систем. Кроме того, они могут быть использованы для прогнозирования и планирования, а также для обучения и обмена знаниями между учеными.

Преимущества математических моделей:

Точность

Возможность экспериментирования в виртуальной среде

Анализ сложных систем

Прогнозирование и планирование

Обучение и обмен знаниями

В заключение, математическая модель играет важную роль в науке, позволяя ученым изучать и анализировать сложные системы, прогнозировать их поведение и принимать обоснованные решения. Она является мощным инструментом, который помогает сделать науку более точной и эффективной.

Видео по теме:

Основные признаки математических моделей

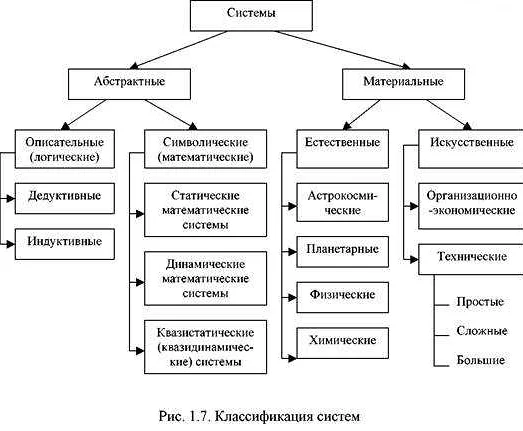
1. Математическое описание. Математическая модель должна быть выражена в виде математических уравнений, функций или алгоритмов. Это позволяет проводить анализ и исследование модели с использованием методов и инструментов математики.

2. Абстракция. Математическая модель является упрощенным представлением реального объекта или процесса. Она удаляет все ненужные детали и фокусируется только на наиболее существенных аспектах. Абстракция позволяет сократить сложность модели и облегчить ее анализ.

3. Определенность. Математическая модель должна быть четко определена и формализована. Каждый элемент модели должен иметь точные математические определения и граничные условия. Это позволяет проводить численное решение модели и получать точные результаты.

4. Предсказательность. Математическая модель должна быть способна предсказывать поведение реального объекта или процесса. Она должна давать качественные и количественные оценки и прогнозы, которые можно сравнивать с экспериментальными или наблюдаемыми данными.

5. Валидация. Математическая модель должна быть проверена и подтверждена на соответствие реальности. Для этого проводятся эксперименты, сравнение с наблюдаемыми данными или другими проверяемыми моделями. Валидация помогает улучшать и проверять точность и надежность модели.

6. Гибкость. Математическая модель должна быть гибкой и адаптивной. Она должна быть способна изменяться в зависимости от изменений входных параметров или условий. Гибкость модели позволяет рассматривать различные сценарии и прогнозировать возможные результаты.

Основные признаки математических моделей определяют их эффективность и применимость в различных областях науки и техники. Правильное использование и анализ математических моделей позволяет получать новые знания и решать практические задачи.

Классификация математических моделей по типу уравнений

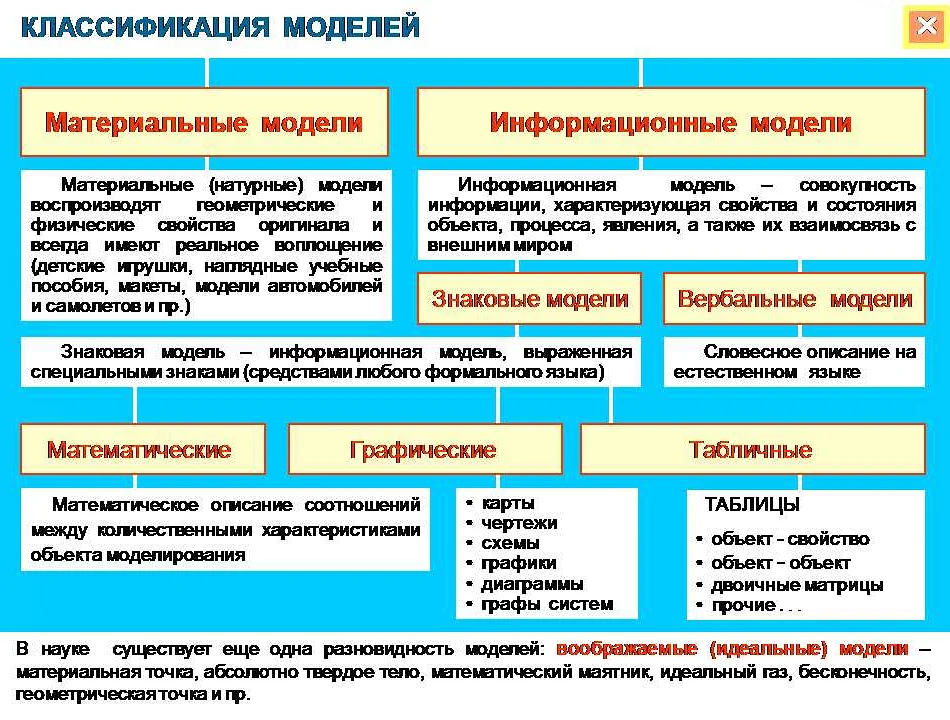
Математические модели могут быть классифицированы по типу уравнений, которые используются в их построении. В зависимости от типа уравнений, математические модели могут быть дифференциальными, интегральными или разностными.

Дифференциальные модели основаны на дифференциальных уравнениях. Эти модели описывают зависимость между функциями и их производными. Дифференциальные модели широко применяются в физике, химии, биологии и других естественных науках, где величины могут меняться в зависимости от времени или других переменных.

Интегральные модели используют интегральные уравнения. Эти модели описывают зависимость между функциями и их интегралами. Интегральные уравнения могут быть использованы для описания статических систем, где значения функций зависят от интегралов от других функций.

Разностные модели основаны на разностных уравнениях. В этих моделях значения функций определены только в дискретных точках. Значения функций в следующих точках определяются на основе значений в предыдущих точках путем использования разностных уравнений. Разностные модели широко применяются в численных методах и компьютерном моделировании.

Классификация математических моделей по типу уравнений позволяет определить подходящие методы решения и алгоритмы для их анализа. В зависимости от типа уравнений, применяются различные математические методы, которые позволяют получить решения и сделать выводы о поведении системы, описываемой моделью.

Классификация математических моделей по структуре

Структура математической модели определяет ее компоненты и взаимосвязи между ними. В зависимости от структуры, математические модели могут быть подразделены на следующие типы:

1. Линейные модели: в таких моделях все компоненты связаны линейными уравнениями. Линейные модели обладают простой структурой и достаточно легко анализируются.

2. Нелинейные модели: в отличие от линейных моделей, в нелинейных моделях компоненты связаны нелинейными уравнениями. Нелинейные модели более сложны в анализе, однако могут более точно описывать реальные процессы.

3. Дискретные модели: в таких моделях значения переменных изменяются только в дискретные моменты времени. Дискретные модели широко используются для моделирования систем, в которых изменение происходит скачкообразно.

4. Непрерывные модели: в отличие от дискретных моделей, в непрерывных моделях значения переменных изменяются непрерывно во времени. Непрерывные модели часто используются для описания физических процессов.

5. Детерминированные модели: в таких моделях значения переменных полностью определяются начальными условиями и параметрами модели. Детерминированные модели не учитывают случайные факторы и шумы.

6. Вероятностные модели: в отличие от детерминированных моделей, вероятностные модели учитывают случайные факторы и шумы. Они основаны на теории вероятностей и статистике.

Таким образом, классификация математических моделей по их структуре позволяет более точно понять их особенности и применимость к конкретным задачам.

Классификация математических моделей по степени абстракции

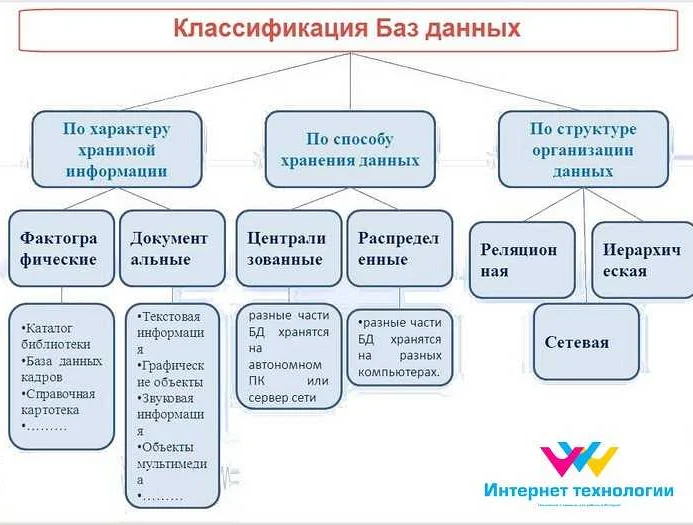
Степень абстракции модели определяется уровнем детализации и уровнем учета реальных факторов и параметров. Чем выше степень абстракции, тем больше упрощений и приближений вносится в модель.

Существует несколько основных типов математических моделей по степени абстракции:

1. Физические модели — это модели, основанные на реальных физических законах и уравнениях. Они полностью описывают физические процессы, учитывая все релевантные факторы и параметры. Физические модели имеют наиболее низкую степень абстракции и могут быть сложными для анализа и решения.

2. Эмпирические модели — это модели, основанные на наблюдениях и экспериментальных данных. Они представляют собой эмпирические законы и зависимости между переменными. Эмпирические модели имеют среднюю степень абстракции и могут быть полезными для прогнозирования и предсказания на основе имеющихся данных.

3. Статистические модели — это модели, основанные на статистическом анализе данных и вероятностных распределениях. Они используются для описания и прогнозирования случайных процессов и явлений. Статистические модели имеют высокую степень абстракции и могут быть полезными для анализа больших объемов данных и определения закономерностей.

Выбор конкретной математической модели с определенной степенью абстракции зависит от целей и требований исследования. Более абстрактные модели позволяют быстро получать результаты, однако могут быть менее точными. Более детализированные модели требуют больше вычислительных ресурсов и времени, но могут предоставить более точные прогнозы и анализ.

Критерии оценки математических моделей

При разработке математических моделей стоит обратить внимание на ряд критериев, позволяющих оценить их качество и применимость в конкретных задачах. Важно выбрать правильные критерии, чтобы получить достоверные результаты и сделать достаточно точные предсказания.

Одним из наиболее распространенных критериев оценки является точность модели. Она позволяет определить, насколько близки значения, полученные с помощью модели, к реальным данным. Чем точнее модель, тем более надежными и полезными будут ее результаты.

Другим важным критерием является адекватность модели. Она оценивается насколько хорошо модель отражает реальные процессы и события. Если модель неадекватна, то она не сможет дать достоверные и полезные результаты, и ее применение будет бесполезно.

Еще одним критерием является простота модели. Чем проще модель, тем проще ее использование и понимание. Слишком сложные модели могут быть трудными для анализа и интерпретации результатов.

Также важным критерием является экономичность модели. Модель должна быть эффективной с точки зрения затрат времени и ресурсов на ее разработку и применение. Чем экономичнее модель, тем легче ее использование и применение в реальных задачах.

Важно отметить, что выбор критериев оценки зависит от конкретной задачи и целей моделирования. Оценка моделей должна быть комплексной, учитывая различные аспекты и требования, чтобы получить наиболее полную и достоверную картину.

Примеры практического применения классификации математических моделей

1. Экономика: Классификация математических моделей применяется в экономике для анализа и прогнозирования различных экономических процессов. Например, модели макроэкономики позволяют изучать поведение экономики в целом и определять влияние различных факторов на уровень инфляции, безработицы, ВВП и других ключевых показателей.

2. Физика: В физике классификация математических моделей используется для описания и предсказания поведения физических систем. Например, модели движения тела под действием силы гравитации позволяют определить его траекторию и скорость в зависимости от начальных условий и параметров системы.

3. Медицина: В медицине математические модели используются для анализа и прогнозирования различных медицинских процессов. Например, модели распространения инфекционных заболеваний позволяют изучать и предсказывать эпидемическую ситуацию, а модели физиологических систем позволяют оценить эффективность лекарственных препаратов и процессов лечения.

4. Инженерия: В инженерии математические модели применяются для анализа и проектирования различных технических систем. Например, модели динамики и прочности материалов позволяют определить оптимальные параметры конструкций, а модели теплопередачи позволяют изучать тепловые процессы и разрабатывать эффективные системы охлаждения.

5. Логистика: В логистике математические модели используются для оптимизации процессов управления и планирования поставок товаров и услуг. Например, модели оптимального маршрута доставки позволяют определить наиболее эффективные маршруты и расписание для доставки грузов, учитывая различные ограничения и требования.

6. Экология: В экологии математические модели применяются для изучения и прогнозирования различных экологических процессов. Например, модели популяционной динамики позволяют оценить влияние изменений в численности и структуре популяций на состояние экосистемы и предсказать возможные последствия вмешательства в природные процессы.

Приведенные примеры демонстрируют разнообразие областей, в которых применяется классификация математических моделей. Она является мощным инструментом для анализа, прогнозирования и оптимизации различных процессов в различных областях науки и практики.

Вопрос-ответ:

Какие основные признаки математических моделей?

Основные признаки математических моделей включают в себя формализацию, абстракцию, представление, описание и анализ. Формализация подразумевает перевод реального явления в математические термины и символы. Абстракция представляет собой упрощение и исключение второстепенных деталей из модели. Представление отображает математическую модель в виде уравнений, графов или других структур. Описание объясняет, как математическая модель связана с реальным явлением. Анализ включает в себя решение уравнений, проведение численных экспериментов и интерпретацию результатов.

Какие критерии используются для классификации математических моделей?

Для классификации математических моделей используются различные критерии, включая: тип модели (например, детерминированная или стохастическая), степень дискретности (непрерывная или дискретная), размерность (одномерная, двумерная, многомерная), уровень абстракции (феноменологическая или механистическая), и метод решения (аналитический или численный).

Чем отличается детерминированная и стохастическая модели?

Детерминированная модель предполагает, что результаты моделирования полностью определяются начальными условиями и заданными параметрами. В этом случае результаты моделирования всегда будут одинаковыми при одинаковых входных данных. Стохастическая модель, напротив, учитывает случайность и вероятностные факторы. Результаты моделирования в стохастической модели будут различаться при разных запусках модели с одинаковыми входными данными.

Какие методы используются для решения математических моделей?

Для решения математических моделей применяются различные методы, включая аналитические и численные. Аналитические методы включают решение уравнений и систем уравнений с помощью алгебраических и дифференциальных методов. Численные методы, напротив, используют компьютерные алгоритмы для приближенного решения уравнений или систем уравнений. Примерами численных методов являются метод конечных разностей, метод конечных элементов и метод Монте-Карло.