Какой тип математических моделей использует алгоритмы

Алгоритмы используют различные типы математических моделей, такие как линейные, нелинейные, стохастические и вероятностные модели. Эти модели позволяют алгоритмам анализировать и предсказывать данные, принимать решения и решать сложные задачи в различных областях, таких как финансы, медицина и технологии.

Математические модели являются важным инструментом для алгоритмов, используемых в различных областях, включая науку, технологии и бизнес. Они позволяют представить сложные системы и процессы в виде математических уравнений и формул, которые можно анализировать и использовать для прогнозирования результатов.

Существует несколько типов математических моделей, которые широко применяются в алгоритмах. Одним из таких типов является статистическая модель, которая основана на анализе статистических данных и предсказывает вероятность событий или взаимосвязь между различными переменными.

Другим типом математической модели является оптимизационная модель, которая используется для нахождения оптимального решения задачи с учетом различных ограничений и целевых функций. Эта модель позволяет найти наилучший вариант из множества возможных решений.

Также существуют дифференциальные модели, которые описывают изменение переменных во времени с помощью дифференциальных уравнений. Эти модели часто применяются для моделирования физических и биологических процессов.

Примером использования математических моделей может служить прогнозирование погоды. С помощью статистической модели можно анализировать исторические данные о погоде и предсказывать вероятность того, что в определенный день будет солнечно или дождливо. Оптимизационная модель может использоваться для определения наиболее эффективного маршрута доставки товаров, учитывая различные факторы, такие как расстояние и стоимость топлива. Дифференциальные модели могут быть использованы для описания распространения инфекционных заболеваний и прогнозирования их развития.

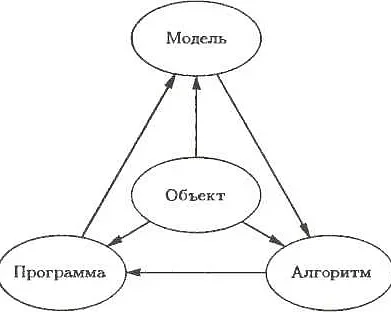
Статические и динамические модели

Математические модели могут быть разделены на две основные категории: статические и динамические.

Статические модели представляют собой аппроксимацию реальных процессов или систем в определенный момент времени. Они не учитывают изменения во времени и рассматривают только текущие состояния объектов или явлений. Такие модели широко применяются в статистике, экономике, социологии и других областях. Например, статическая модель может использоваться для описания распределения доходов в определенной стране на основе текущих данных.

Динамические модели учитывают изменения во времени и позволяют предсказывать поведение системы в будущем. Они описывают эволюцию процессов и объектов во времени с учетом различных факторов и взаимодействий. Динамические модели широко используются в физике, биологии, инженерии и других науках для изучения движения, эволюции и развития систем. Например, динамическая модель может использоваться для предсказания популяционной динамики популяции животных в определенной экосистеме.

Оба типа моделей имеют свои преимущества и ограничения, и выбор между статической и динамической моделью зависит от конкретной задачи и целей исследования.

Детерминированные и стохастические модели

Математические модели могут быть разделены на две основные категории: детерминированные и стохастические модели.

Детерминированные модели представляют собой системы уравнений, которые описывают взаимодействие между различными переменными. В этом типе моделей значения переменных полностью определяются начальными условиями и параметрами модели. Детерминированные модели используются для предсказания поведения системы в будущем на основе известных данных и законов, управляющих этой системой.

Стохастические модели, напротив, учитывают случайность и неопределенность в данных. Они используются для моделирования систем, где результаты могут варьироваться из-за случайных факторов. В таких моделях переменные представлены вероятностными распределениями, а изменение этих переменных во времени определяется случайными событиями.

Выбор между детерминированными и стохастическими моделями зависит от природы системы, которую нужно изучить, и доступности данных. Детерминированные модели чаще используются в случаях, когда данные являются точными и предсказуемыми, а стохастические модели применяются, когда имеются случайные факторы, которые могут влиять на результаты.

Примером детерминированной модели может быть модель шаровой системы, где движение каждого шарика определяется определенными законами физики и начальными условиями. В то время как стохастическая модель может использоваться для моделирования финансовых рынков, где цены акций могут изменяться из-за случайных факторов, таких как новости или события.

Линейные и нелинейные модели

Линейные модели являются простыми и понятными. Они основаны на предположении, что зависимость между переменными является линейной. В линейных моделях используется линейная функция, которая связывает входные данные с выходными. Примерами линейных моделей являются линейная регрессия и линейный классификатор.

Нелинейные модели более гибки и могут учитывать более сложные зависимости между переменными. Они позволяют использовать нелинейные функции для описания взаимодействия между данными. Нелинейные модели могут быть полиномиальными, экспоненциальными, сигмоидальными и другими. Примерами нелинейных моделей являются полиномиальная регрессия, нейронные сети и метод опорных векторов.

Выбор между линейными и нелинейными моделями зависит от специфики задачи и данных. Если зависимость между переменными является простой и линейной, то линейные модели могут быть более эффективными и интерпретируемыми. Однако, если данные имеют сложную нелинейную структуру, то нелинейные модели могут показать лучшие результаты.

Использование линейных и нелинейных моделей дает алгоритмам возможность адаптироваться к различным типам данных и задачам, и выбор между ними является важным шагом при построении математических моделей.

Дискретные и непрерывные модели

Математические модели могут быть разделены на две основные категории: дискретные и непрерывные модели.

Дискретные модели используются для описания систем, где значения переменных могут принимать только конкретные значения. Например, модели компьютерных сетей, где количество пакетов данных, передаваемых между узлами, может быть только целым числом. Дискретные модели также используются в теории вероятностей и статистике для моделирования случайных процессов с конечным или счетным множеством исходов.

Непрерывные модели, напротив, предназначены для описания систем, где значения переменных могут принимать любые значения в определенном диапазоне. Например, модели физических процессов, таких как движение тела, температура воздуха или электромагнитные поля. Непрерывные модели часто используются в физике, инженерии и других областях науки, где наблюдаются непрерывные изменения величин.

Выбор между дискретной и непрерывной моделью зависит от характера системы и уровня детализации, необходимого для достижения поставленных целей. Оба типа моделей имеют свои преимущества и ограничения, и выбор определенного типа модели должен быть обоснован исходя из конкретной задачи.

Эмпирические и аналитические модели

Математические модели используются для представления реальных систем и явлений в виде формальных математических уравнений. Существуют различные типы математических моделей, включая эмпирические и аналитические модели.

Эмпирические модели основаны на экспериментальных данных и наблюдениях. Они позволяют описать связь между входными и выходными параметрами системы, но не имеют строгой математической основы. Эмпирические модели часто используются в исследованиях, когда недостаточно данных или знаний о системе для создания точной аналитической модели.

Аналитические модели, напротив, основываются на математических уравнениях и законах. Они представляют систему в виде аналитических выражений и позволяют проводить точные математические рассуждения. Аналитические модели являются более формальными и точными, поэтому они широко используются в науке и инженерии для прогнозирования поведения системы и оптимизации ее параметров.

Примеры эмпирических моделей включают статистические модели, регрессионные модели, нейронные сети и генетические алгоритмы. Эти модели основаны на анализе данных и позволяют предсказывать будущие значения системы на основе ее прошлого поведения.

Аналитические модели включают дифференциальные уравнения, уравнения в частных производных, алгебраические уравнения и другие математические выражения. Они представляют систему в виде точных математических формул, что позволяет проводить аналитические вычисления и изучать ее свойства.

В зависимости от конкретной задачи и доступных данных, выбор между эмпирическими и аналитическими моделями может быть сложным. В некоторых случаях, когда у нас есть достаточно данных и знаний о системе, предпочтительно использовать аналитические модели для получения точных результатов. В других случаях, когда данных недостаточно или система слишком сложна для описания аналитическими методами, эмпирические модели могут быть более подходящим выбором.

Примеры использования математических моделей в алгоритмах

Математические модели играют важную роль в разработке алгоритмов в различных областях. Вот несколько примеров использования математических моделей:

ОбластьПример математической моделиПрименение

Финансы	Модель Блэка-Шоулза	Определение стоимости опционов на финансовых рынках
Транспорт	Модель минимального остовного дерева	Оптимальное планирование маршрутов доставки
Медицина	Модель СИМПТОМ	Диагностика и прогнозирование заболеваний
Искусственный интеллект	Модель нейронной сети	Распознавание образов, голосов, обучение с подкреплением

Это лишь некоторые примеры, и математические модели могут применяться во многих других областях. Они позволяют алгоритмам анализировать и предсказывать различные явления и принимать более обоснованные решения.

Вопрос-ответ:

Какие типы математических моделей существуют?

Существует несколько типов математических моделей, которые используются в алгоритмах. Некоторые из них включают дискретные модели, непрерывные модели, стохастические модели, оптимизационные модели и графовые модели.

Можете ли дать примеры использования дискретных математических моделей в алгоритмах?

Конечные автоматы и графы являются примерами дискретных математических моделей, используемых в алгоритмах. Они могут использоваться для моделирования процессов, в которых состояния системы меняются дискретно.

Какие примеры непрерывных математических моделей вы можете привести?

Дифференциальные уравнения являются примерами непрерывных математических моделей, используемых в алгоритмах. Они могут использоваться для моделирования физических процессов, таких как движение тела или изменение концентрации вещества во времени.

Какие типы математических моделей используются для моделирования случайных процессов?

Статистические и вероятностные модели являются типами математических моделей, используемых для моделирования случайных процессов. Они могут использоваться для описания случайных событий и предсказания их вероятностей.

В каких случаях можно использовать графовые модели в алгоритмах?

Графовые модели могут использоваться в алгоритмах для моделирования связей и взаимодействий между объектами или сущностями. Они широко применяются в областях таких как сети, логистика, социальные сети и многие другие.

Какие типы математических моделей используются алгоритмами?

Алгоритмы могут использовать различные типы математических моделей, включая линейные модели, нелинейные модели, статистические модели, графовые модели и др.

Можете привести примеры математических моделей, которые используются алгоритмами?

Конечно! Некоторые примеры математических моделей, используемых алгоритмами, включают линейную регрессию, логистическую регрессию, деревья решений, графовые модели, нейронные сети и многое другое.

Видео по теме: