Конгруэнтность в математике что это

Конгруэнтность в математике – понятие, описывающее взаимное соответствие чисел по модулю. Узнайте, что такое конгруэнтность, как ее применять и какие свойства она имеет.

Конгруэнтность — это понятие, которое широко используется в математике для описания отношения между двумя числами. В простых терминах, два числа считаются конгруэнтными, если они имеют одинаковый остаток при делении на определенное число, которое называется модулем. Конгруэнтность часто используется в различных областях математики, таких как алгебра, теория чисел и криптография.

Одним из ключевых свойств конгруэнтности является то, что она образует отношение эквивалентности между числами. Это означает, что она удовлетворяет трем основным свойствам: рефлексивности, симметричности и транзитивности. То есть, каждое число конгруэнтно самому себе, если два числа конгруэнтны, то они взаимно конгруэнтны, и если два числа конгруэнтны и второе число конгруэнтно третьему числу, то первое число также конгруэнтно третьему числу.

Применение конгруэнтности в математике находится во многих областях. В алгебре, конгруэнтность используется для определения классов вычетов и построения алгебраических структур, таких как кольца и поля. В теории чисел, конгруэнтность играет важную роль в решении уравнений и изучении свойств простых чисел. В криптографии, конгруэнтность используется для создания и анализа различных алгоритмов шифрования и подписи.

Таким образом, конгруэнтность является важным понятием в математике, которое позволяет изучать и решать различные проблемы и задачи. Понимание этого понятия и его применения может быть полезным для студентов и исследователей, занимающихся математикой и ее приложениями.

Что такое конгруэнтность в математике и как она применяется?

Применение конгруэнтности в математике широко распространено. Она используется в алгебре, теории чисел, криптографии и других областях.

Основное применение конгруэнтности связано с решением задач на остатки. Когда требуется найти все числа, удовлетворяющие определенным условиям с точностью до конгруэнтности, конгруэнтность позволяет сократить количество возможных решений и упростить задачу.

Конгруэнтность также используется в арифметических операциях с остатками. Например, с помощью конгруэнтности можно выполнять сложение, вычитание, умножение и деление по модулю. Это позволяет упростить вычисления и получить результаты с меньшими числовыми значениями.

Кроме того, конгруэнтность играет важную роль в криптографии. Она используется для создания безопасных алгоритмов шифрования, генерации случайных чисел и проверки целостности данных.

В заключение, конгруэнтность — это мощный инструмент математики, который позволяет упростить вычисления, решать задачи на остатки и обеспечивать безопасность информации. Понимание и применение конгруэнтности имеет широкие практические применения и является неотъемлемой частью современной математики.

Видео по теме:

Определение и основные понятия

Конгруэнтность может быть определена как отношение эквивалентности между двумя объектами, которое обозначает, что эти объекты совпадают или эквивалентны друг другу в некотором смысле. В математике, особенно в алгебре и теории чисел, конгруэнтность обычно определяется на основе равенства по модулю некоторого числа.

Основные понятия, связанные с конгруэнтностью, включают:

ТерминОписание

Класс вычетов	Множество всех чисел, которые эквивалентны друг другу по модулю заданного числа.
Остаток	Число, которое остается после деления одного числа на другое.
Конгруэнтное уравнение	Уравнение, в котором ищется значение, удовлетворяющее условию равенства по модулю.
Конгруэнтный класс	Множество всех чисел, эквивалентных друг другу по модулю.

Понимание конгруэнтности и основных понятий, связанных с ней, является важным для решения различных математических задач, включая нахождение решений уравнений, работы с остатками и вычислений по модулю.

Арифметическая конгруэнтность

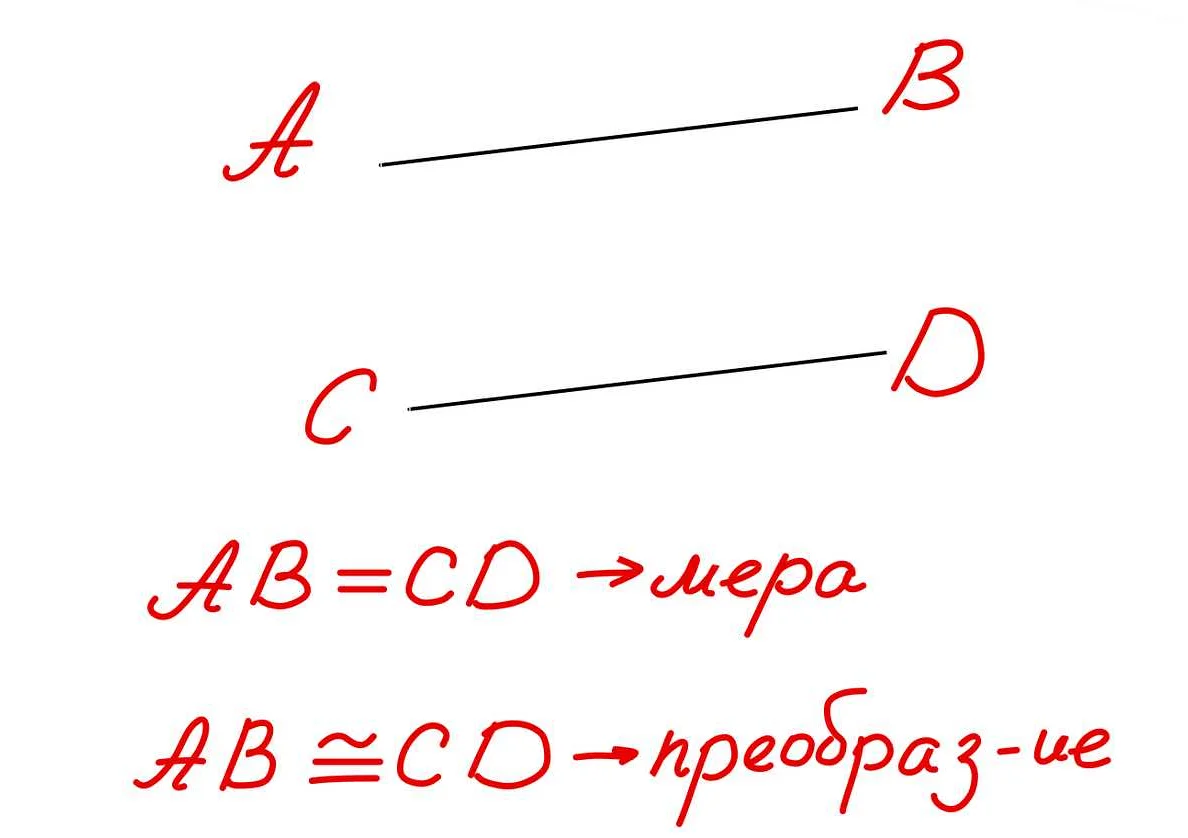
Обозначение арифметической конгруэнтности: a ≡ b (mod n), где a и b — числа, модуль n — положительное число.

Примеры:

1. 12 ≡ 2 (mod 5), так как разность 12 — 2 = 10 делится нацело на 5.

2. 25 ≡ 7 (mod 6), так как разность 25 — 7 = 18 делится нацело на 6.

Арифметическая конгруэнтность находит применение в различных областях математики, включая теорию чисел, криптографию и алгебру. Это понятие позволяет решать задачи, связанные с вычислениями по модулю и работой с остатками от деления.

Конгруэнтность по модулю

Обозначается конгруэнтность по модулю символом ≡ (три знака равенства). Таким образом, если a и b – два числа, а m – модуль, то запись a ≡ b (mod m) означает, что a и b сравнимы по модулю m.

Конгруэнтность по модулю широко применяется в различных областях математики и информатики. Она позволяет решать уравнения и системы уравнений, основываясь на свойствах конгруэнтности. Также конгруэнтность используется в криптографии для защиты информации и создания шифровальных алгоритмов.

Например, чтобы найти остаток от деления большого числа на малое, можно воспользоваться свойством конгруэнтности по модулю. Также с помощью конгруэнтности можно решать уравнения вида a ≡ b (mod m) и находить решения в ограниченном интервале.

Конгруэнтность по модулю имеет множество свойств и правил, которые позволяют выполнять различные операции с конгруэнтными числами, такие как сложение, вычитание, умножение и возведение в степень. Такие операции позволяют упростить вычисления и сделать их более эффективными.

В заключение, конгруэнтность по модулю является важным понятием в математике, которое широко применяется в различных областях. Она позволяет упростить вычисления, решать уравнения и создавать алгоритмы защиты информации.

Конгруэнтность в алгебре

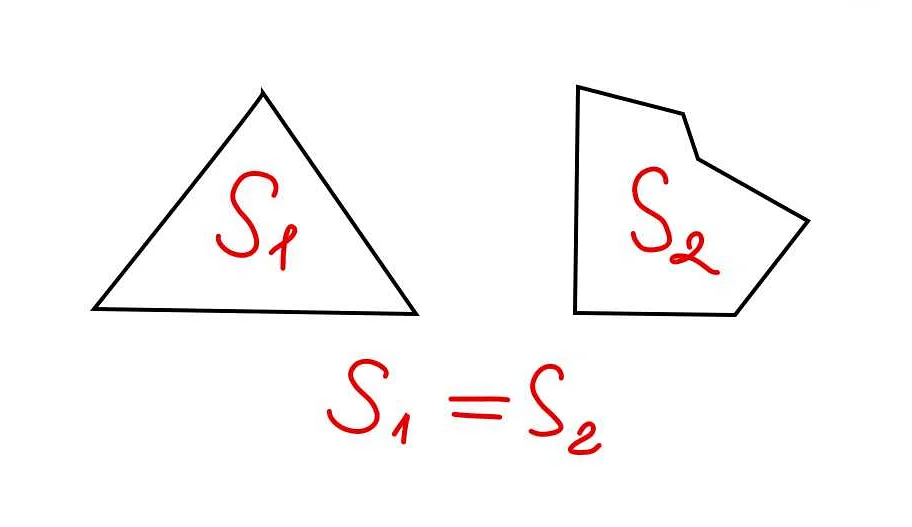
Два числа считаются конгруэнтными по модулю, если они имеют одинаковый остаток при делении на заданное число, называемое модулем. Обозначается это отношение символом ≡.

Конгруэнтность в алгебре позволяет заменять одни числа другими, если они конгруэнтны по модулю. Например, если два числа a и b считаются конгруэнтными по модулю m, то можно заменить одно число на другое в алгебраических выражениях и уравнениях без изменения результата.

Конгруэнтность в алгебре находит свое применение в решении систем уравнений, расчетах по модулю, криптографии и других областях математики и информатики. Она позволяет упростить вычисления и установить определенные свойства чисел и операций над ними.

Таблица ниже показывает примеры конгруэнтности для разных модулей и целых чисел:

Модуль (m)Целое число (a)Целое число (b)Конгруэнтность (a ≡ b mod m)

5	7	2	7 ≡ 2 mod 5
10	15	25	15 ≡ 25 mod 10
3	8	17	8 ≡ 17 mod 3

Все числа, указанные в таблице, конгруэнтны друг другу по соответствующему модулю.

Применение конгруэнтности в криптографии

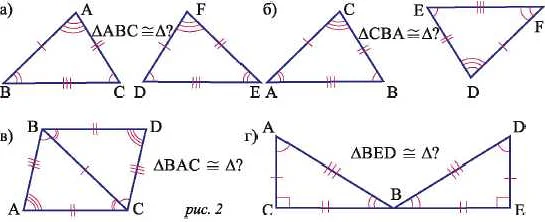
Одним из способов применения конгруэнтности в криптографии является использование арифметических операций над остатками. Для этого используется алгебраическая структура, называемая кольцом вычетов по модулю.

ПримерОписание

a ≡ b (mod n)	Остаток от деления числа a на n равен остатку от деления числа b на n
a + b ≡ c (mod n)	Сумма остатков от деления чисел a и b на n равна остатку от деления числа c на n
a * b ≡ c (mod n)	Произведение остатков от деления чисел a и b на n равно остатку от деления числа c на n

Такие операции позволяют использовать конгруэнтность для создания криптографических алгоритмов, таких как шифр RSA. Шифр RSA основан на сложности факторизации больших чисел и применяет конгруэнтность для шифрования и дешифрования сообщений.

Кроме того, конгруэнтность применяется для проверки подлинности и целостности данных, используя хэш-функции. Хэш-функция — это функция, которая преобразует входные данные произвольной длины в фиксированный выходной хэш-код. При использовании конгруэнтности, можно проверить, является ли полученный хэш-код равным ожидаемому, что позволяет обнаружить любые изменения данных.

Таким образом, применение конгруэнтности в криптографии позволяет обеспечить безопасность и надежность шифрования данных, а также проверку их подлинности и целостности.

Конгруэнтность в теории чисел

Два числа называются конгруэнтными по модулю, если их разность делится на это модуль. Формально, для чисел a, b и модуля m, a и b считаются конгруэнтными по модулю m, если a ≡ b (mod m).

Конгруэнтность в теории чисел широко применяется в различных областях математики и информатики. Она является основой для решения задач, связанных с делением на модуль и поиском остатка. Кроме того, конгруэнтность используется в криптографии, теории кодирования, алгоритмах проверки контрольных сумм и т.д.

Конгруэнтность позволяет упростить вычисления и установить зависимости между числами, основываясь на их остатках от деления на модуль. Она является мощным инструментом для анализа и решения задач, связанных с арифметическими операциями.

Таким образом, конгруэнтность в теории чисел играет важную роль и представляет собой важный инструмент для решения различных задач, связанных с числами и их взаимоотношениями.

Примеры задач и решений

Для лучшего понимания конгруэнтности в математике, рассмотрим несколько примеров задач и их решений:

Пример задачиРешение

1. Доказать, что если два числа имеют одинаковый остаток при делении на некоторое число, то их разность также имеет этот же остаток.	Пусть числа a и b имеют одинаковый остаток r при делении на число m. Это означает, что существуют целые числа k1 и k2, такие что a = k1m + r и b = k2m + r. Вычтем эти выражения: a — b = (k1m + r) — (k2m + r) = (k1 — k2)m + 0 = (k1 — k2)m. Таким образом, a — b делится на m без остатка, а значит имеет тот же остаток r.
2. Найти все целые числа, которые имеют остаток 2 при делении на 5 и остаток 3 при делении на 7.	Чтобы найти такие числа, нужно решить систему сравнений: x ≡ 2 (mod 5) и x ≡ 3 (mod 7). Используя китайскую теорему об остатках, получаем x ≡ 17 (mod 35). Таким образом, все целые числа вида 35k + 17, где k — целое число, удовлетворяют условиям задачи.
3. Найти наименьшее положительное целое число, квадрат которого имеет остаток 3 при делении на 5 и остаток 4 при делении на 7.	Аналогично предыдущему примеру, решаем систему сравнений: x^2 ≡ 3 (mod 5) и x^2 ≡ 4 (mod 7). Найденное ранее решение x ≡ 17 (mod 35) не подходит, так как 17^2 ≡ 2 (mod 5). Используя китайскую теорему об остатках, получаем x ≡ 52 (mod 35). Наименьшее положительное целое число, удовлетворяющее этому условию, равно 52.

Приведенные примеры задач помогут вам лучше понять, как применяется конгруэнтность в математике и как решать задачи, связанные с ней.

Вопрос-ответ:

Что такое конгруэнтность в математике?

Конгруэнтность в математике — это отношение эквивалентности на целых числах, определяемое с помощью операции модуля. Два числа считаются конгруэнтными по модулю, если их разность делится на это модуль без остатка.

Какая роль конгруэнтности в математике?

Конгруэнтность играет важную роль в различных областях математики, таких как теория чисел, алгебра и криптография. Она позволяет сравнивать числа и устанавливать их свойства, основываясь на их остатках при делении на определенное число.

Какие основные свойства конгруэнтности?

Основные свойства конгруэнтности включают рефлексивность (число конгруэнтно самому себе), симметричность (если число A конгруэнтно числу B, то число B конгруэнтно числу A) и транзитивность (если число A конгруэнтно числу B, и число B конгруэнтно числу C, то число A конгруэнтно числу C).

В каких областях математики применяется конгруэнтность?

Конгруэнтность широко применяется в различных областях математики, таких как теория чисел, алгебра, геометрия и криптография. В теории чисел, например, она используется для решения уравнений с модулями, изучения свойств простых чисел и поиска сравнительных характеристик чисел.

Как конгруэнтность применяется в криптографии?

Конгруэнтность имеет важное значение в криптографии, особенно в симметричных алгоритмах шифрования. Она используется для защиты информации и обеспечения безопасности данных. Например, в алгоритме RSA конгруэнтность применяется для генерации ключей и шифрования сообщений.