Что такое кортеж в математике
Содержимое
- 1 Что такое кортеж в математике
- 1.1 Что такое кортеж в математике?
- 1.2 Определение и примеры использования кортежа
- 1.3 Простые и составные кортежи
- 1.4 Размерность и порядок элементов в кортеже
- 1.5 Понятие упорядоченной пары в математике
- 1.6 Примеры использования упорядоченной пары
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.9 Определение n-мерного кортежа
- 1.10 Примеры использования n-мерного кортежа
Кортеж в математике — это упорядоченный набор элементов, где каждый элемент имеет свою позицию в кортеже. Он отличается от множества и последовательности, так как может содержать повторяющиеся элементы и имеет определенный порядок. Узнайте больше о кортежах и их применении в математике.
Кортеж – это математическая структура данных, представляющая собой упорядоченный набор элементов. Он отличается от множества и последовательности тем, что его элементы могут быть различных типов и могут повторяться. Каждый элемент кортежа имеет свой порядковый номер, который позволяет однозначно идентифицировать его в наборе.
Кортежи широко используются в различных областях математики и информатики. Например, в комбинаторике они используются для представления перестановок и сочетаний элементов. В теории множеств и логике кортежи могут служить для задания отношений между элементами. В программировании кортежи используются для упорядоченного хранения данных, передачи параметров функциям и множественного возврата значений из функций.
Например, в математике кортеж {1, 2, 3} может представлять собой упорядоченный набор трех чисел. В программировании кортеж (1, «apple», True) может представлять собой упорядоченный набор значения целого числа, строки и логического значения.
Кортежи могут быть созданы и изменены с помощью различных операций, таких как добавление и удаление элементов, слияние и разделение кортежей. Операции над кортежами позволяют эффективно работать с данными и проводить различные вычисления и анализы.
Что такое кортеж в математике?
Кортежи широко используются в математике, особенно в теории множеств и алгебре. Они позволяют компактно представить информацию и облегчают работу с наборами данных.
Каждый элемент кортежа называется компонентом. Например, кортеж (1, 2, 3) состоит из трех компонентов: 1, 2 и 3. Компоненты могут быть любого типа данных, включая числа, буквы, строки и другие кортежи.
Кортежи могут быть использованы для представления различных объектов и связей. Например, в геометрии можно использовать кортежи для представления точек, прямых или плоскостей. В алгебре кортежи могут использоваться для представления векторов или матриц.
Операции над кортежами включают создание новых кортежей, изменение их компонентов, объединение или разделение кортежей, а также сравнение их между собой. Кортежи также могут быть использованы в качестве аргументов и возвращаемых значений функций.
Определение и примеры использования кортежа

Примером использования кортежа может служить представление координат точки на плоскости. Например, чтобы представить точку с координатами (3, 4), можно использовать кортеж (3, 4). Каждая координата представлена отдельным элементом кортежа.
Кортежи могут содержать элементы различных типов данных. Например, можно создать кортеж, содержащий целое число, строку и вещественное число: (42, «hello», 3.14). В этом случае каждый элемент будет иметь свой индекс, начиная с нуля: 0 для числа 42, 1 для строки «hello» и 2 для числа 3.14.
Кортежи могут быть использованы для передачи нескольких значений в функцию или для возврата нескольких значений из функции. Например, функция, вычисляющая площадь и периметр прямоугольника, может возвращать кортеж из двух значений: (площадь, периметр).
Также кортежи могут использоваться для создания структур данных, например, для представления записи в базе данных или для хранения информации о студенте (имя, фамилия, возраст и т. д.). Кортежи обеспечивают удобный доступ к элементам и позволяют эффективно работать с ними.
Простые и составные кортежи
В математике существуют два типа кортежей: простые и составные.
Простой кортеж представляет собой упорядоченный набор элементов, который не может быть разбит на более мелкие части. Примеры простых кортежей:
ПримерОписание
| (1, 2, 3) | Простой кортеж из трёх элементов |
| (a, b) | Простой кортеж из двух элементов |
| (x) | Простой кортеж из одного элемента |
Составной кортеж состоит из нескольких простых кортежей и может быть разделён на более мелкие составные части. Примеры составных кортежей:
ПримерОписание
| ((1, 2), (3, 4)) | Составной кортеж, состоящий из двух простых кортежей |
| ((a, b), (c, d)) | Составной кортеж, состоящий из двух простых кортежей |
| (((x), y), z) | Составной кортеж, состоящий из трёх простых кортежей |
Простые и составные кортежи могут быть использованы в различных математических операциях и алгоритмах для представления упорядоченных данных.
Размерность и порядок элементов в кортеже
Кортеж в математике представляет собой упорядоченный набор элементов, где каждый элемент имеет свое место и порядок. Размерность кортежа определяет количество элементов в наборе.
Например, кортеж из двух элементов (2-мерный кортеж) может быть представлен в виде (x, y), где x и y — элементы, которые могут быть числами, буквами или любыми другими объектами. Кортежи могут также иметь большую размерность, например, трехмерный кортеж (x, y, z), где z — третий элемент.
Порядок элементов в кортеже имеет значение и определяет их положение в наборе. Например, в двухмерном кортеже (x, y) порядок элементов важен: сначала идет x, а затем y. Если поменять порядок элементов, получим другой кортеж.
Размерность и порядок элементов в кортеже могут иметь важное значение при решении математических задач и анализе данных. Они позволяют упорядочить информацию и проводить операции с каждым элементом набора в нужном порядке.
Понятие упорядоченной пары в математике

Формально, упорядоченная пара записывается в виде (a, b), где a и b — элементы пары. Порядок в паре имеет значение, поэтому (a, b) и (b, a) считаются различными парами. Например, пара (2, 3) отличается от пары (3, 2).
Упорядоченные пары широко используются в математике для представления различных объектов, таких как точки на плоскости, векторы, множества и другие. Они могут быть использованы для удобного описания отношений между объектами и для решения различных задач.
Например, в геометрии упорядоченная пара (x, y) может представлять точку на плоскости, где x — координата по горизонтали (ось X), а y — координата по вертикали (ось Y). Векторы могут быть представлены упорядоченными парами, где первый элемент — это длина вектора, а второй элемент — его направление.
Также упорядоченные пары могут использоваться для представления отношений между объектами. Например, пара (a, b) может представлять отношение «a является предком b» или «b является наследником a».
Важно отметить, что упорядоченные пары могут быть вложены друг в друга, образуя так называемые кортежи. Например, (x, y, z) может представлять точку в трехмерном пространстве, где x, y и z — координаты по осям X, Y и Z соответственно.
Таким образом, понятие упорядоченной пары является важным для представления упорядоченных данных в математике и находит широкое применение в различных областях.
Примеры использования упорядоченной пары
Кортежи, или упорядоченные пары, находят широкое применение в различных областях математики и информатики. Рассмотрим несколько примеров использования упорядоченной пары:
1. Координаты точки: упорядоченная пара (x, y) может использоваться для задания координат точки на плоскости. Например, в математическом анализе координаты точки могут использоваться для определения ее положения на графике функции.
2. Шифрование информации: упорядоченные пары могут использоваться для шифрования информации. Например, в криптографии элементы ключа шифрования могут быть представлены в виде упорядоченных пар.
3. Базы данных: в базах данных упорядоченные пары могут использоваться для представления связей между различными сущностями. Например, в реляционных базах данных упорядоченные пары могут использоваться для представления связи между таблицами.
ПримерОписание
| 4. Графы | Упорядоченные пары могут использоваться для представления связей между вершинами графа. Например, в теории графов упорядоченные пары могут использоваться для определения ребер графа. |
| 5. Множества | Упорядоченные пары могут использоваться для представления элементов множества. Например, в теории множеств упорядоченные пары могут использоваться для определения упорядоченных пар элементов множества. |
Видео по теме:
Вопрос-ответ:
Что такое кортеж в математике?
Кортеж в математике — это упорядоченный набор элементов, которые могут быть любого типа данных. В отличие от множества, порядок элементов в кортеже имеет значение.
Какой смысл имеет использование кортежей в математике?
Использование кортежей в математике позволяет упорядочить и структурировать данные. Они часто используются для представления координат точек на плоскости или в пространстве, записи последовательностей чисел или символов.
Какая разница между множеством и кортежем в математике?
Основное отличие между множеством и кортежем в математике заключается в том, что порядок элементов в кортеже имеет значение, в то время как порядок элементов в множестве не имеет значения. Кроме того, элементы множества должны быть уникальными, в то время как элементы кортежа могут повторяться.
Какие примеры использования кортежей в математике?
Кортежи могут использоваться для представления координат точек на плоскости или в пространстве, записи последовательностей чисел или символов, хранения информации о структуре данных и многих других задач. Например, кортежи могут быть использованы для представления данных о погоде (температура, влажность, давление) или для хранения информации о студентах (имя, фамилия, возраст).
Как можно создать и использовать кортежи в математике?
Для создания кортежа в математике можно использовать круглые скобки, в которых перечисляются элементы кортежа через запятую. Например, (1, 2, 3) — кортеж из трех элементов. Для доступа к элементам кортежа можно использовать индексацию, начиная с 0. Например, для доступа к первому элементу кортежа можно использовать выражение «кортеж[0]».
Определение n-мерного кортежа
Одномерный кортеж или 1-мерный кортеж – это простой набор элементов, который имеет только одно измерение. Например, кортеж (1, 2, 3) является одномерным кортежем.
Двумерный кортеж или 2-мерный кортеж – это набор элементов, который имеет два измерения. Каждый элемент двумерного кортежа представляет собой одномерный кортеж. Например, кортеж ((1, 2), (3, 4)) является двумерным кортежем.
Аналогично можно определить и n-мерный кортеж, где n – количество измерений. Каждый элемент n-мерного кортежа представляет собой (n-1)-мерный кортеж. Например, кортеж (((1, 2), (3, 4)), ((5, 6), (7, 8))) является трехмерным кортежем.
Кортежи широко используются в математике и программировании для представления и обработки упорядоченных данных. Они позволяют компактно хранить информацию и обеспечивают удобный доступ к ее элементам.
Примеры использования n-мерного кортежа

Кортежи широко используются в математике для представления и сравнения наборов данных, как в двумерном, так и в многомерном пространстве. Ниже приведены некоторые примеры использования n-мерного кортежа:
ПримерОписание
| (3, 4) | Двумерный кортеж, представляющий точку с координатами x = 3 и y = 4. |
| (1, 2, 3) | Трехмерный кортеж, представляющий точку в трехмерном пространстве с координатами x = 1, y = 2 и z = 3. |
| (0, 1, 0, 1) | Четырехмерный кортеж, представляющий точку в четырехмерном пространстве. |
| (1, 1, 2, 3, 5) | Пятимерный кортеж, представляющий набор пяти чисел. |
Кортежи позволяют компактно и эффективно представлять наборы данных в математике и других областях, таких как программирование и анализ данных. Они используются для хранения и сравнения координат, значений, векторов и других структур данных.

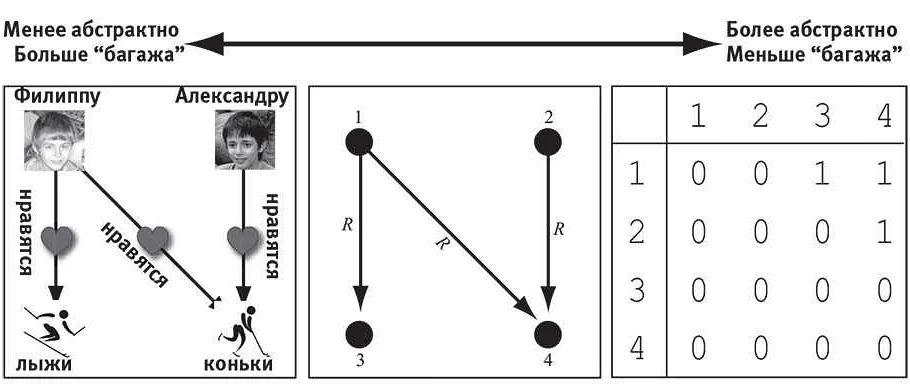


Концепция кортежа в математике – это уникальный и мощный инструмент, который позволяет представить несколько элементов в виде одной структуры. Кортежи обладают непревзойденной гибкостью и широким спектром применения в различных областях математики. Например, в геометрии кортежи могут использоваться для задания координат точек на плоскости или в пространстве. В алгебре кортежи позволяют представить наборы чисел или переменных и выполнять с ними различные операции, такие как сложение или умножение. Кроме того, кортежи могут быть полезны при работе с матрицами, векторами и другими структурами данных. Открытие и использование кортежей в математике открывает новые возможности для решения сложных задач и расширяет границы наших знаний.
Статья очень понравилась! Я долго искала информацию о кортежах в математике, и эта статья оказалась очень полезной и информативной. Она дает ясное определение кортежа и приводит различные примеры его использования. Я теперь лучше понимаю, как можно использовать кортежи для хранения и представления данных. Это знание будет полезным для моей работы в сфере анализа данных. Я также оценила приведенные примеры кода на Python, они помогли мне лучше понять, как использовать кортежи в практических задачах. Большое спасибо автору за такую полезную информацию! Я рекомендую эту статью всем, кто хочет узнать больше о кортежах в математике.