Круги эйлера как решать задачи по математике

Круги Эйлера — это мощный инструмент в решении математических задач. Узнайте, как использовать их для решения сложных задач по математике и улучшите свои навыки в этой области.

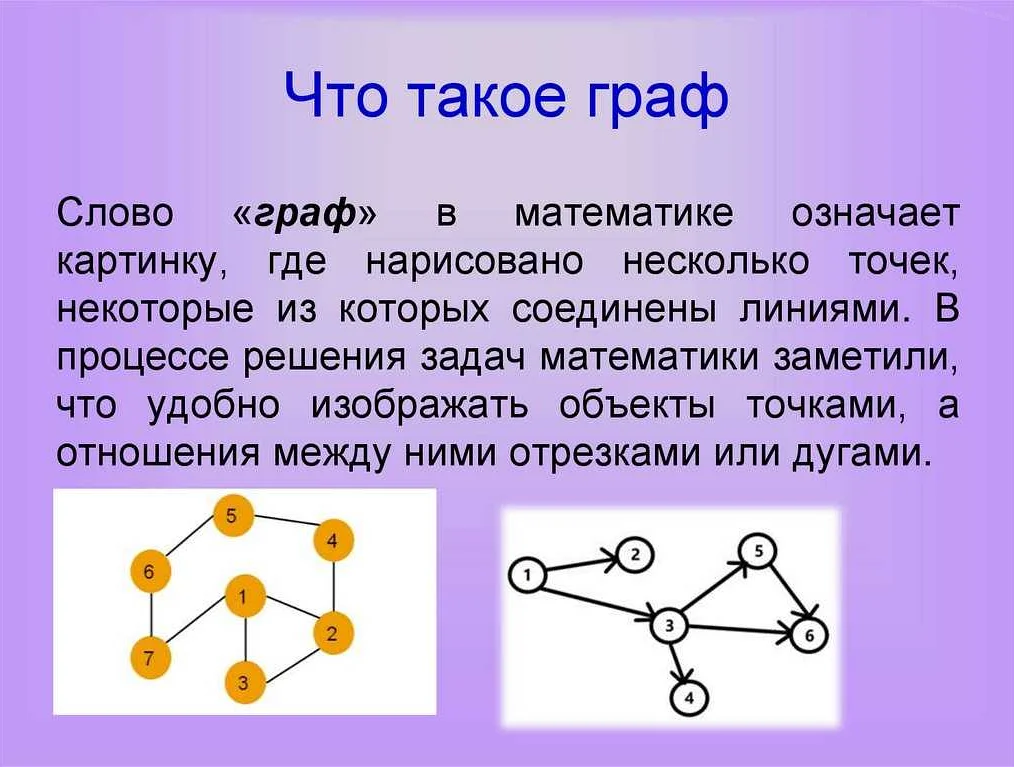
Круги Эйлера – это одна из самых интересных и полезных тем в математике. Они позволяют решать разнообразные задачи, связанные с графами и комбинаторикой. Основная идея заключается в том, чтобы найти пути, которые проходят по каждому ребру графа ровно один раз.

Одним из самых известных примеров применения кругов Эйлера являются задачи о поиске эффективных маршрутов для обхода нескольких городов или пунктов. Например, предположим, что у нас есть несколько городов, и мы хотим найти кратчайший путь, который пройдет через каждый город ровно один раз.

Круги Эйлера также находят применение в других областях математики, таких как теория графов, теория игр, криптография и даже в биологии. Это мощный инструмент, который позволяет решать сложные задачи и находить оптимальные решения.

В данной статье мы рассмотрим различные методы решения задач с использованием кругов Эйлера, а также приведем примеры их применения в реальной жизни. Надеемся, что эта информация будет полезной для всех, кто интересуется математикой и хочет научиться решать задачи более эффективно.

Понятие и применение кругов Эйлера

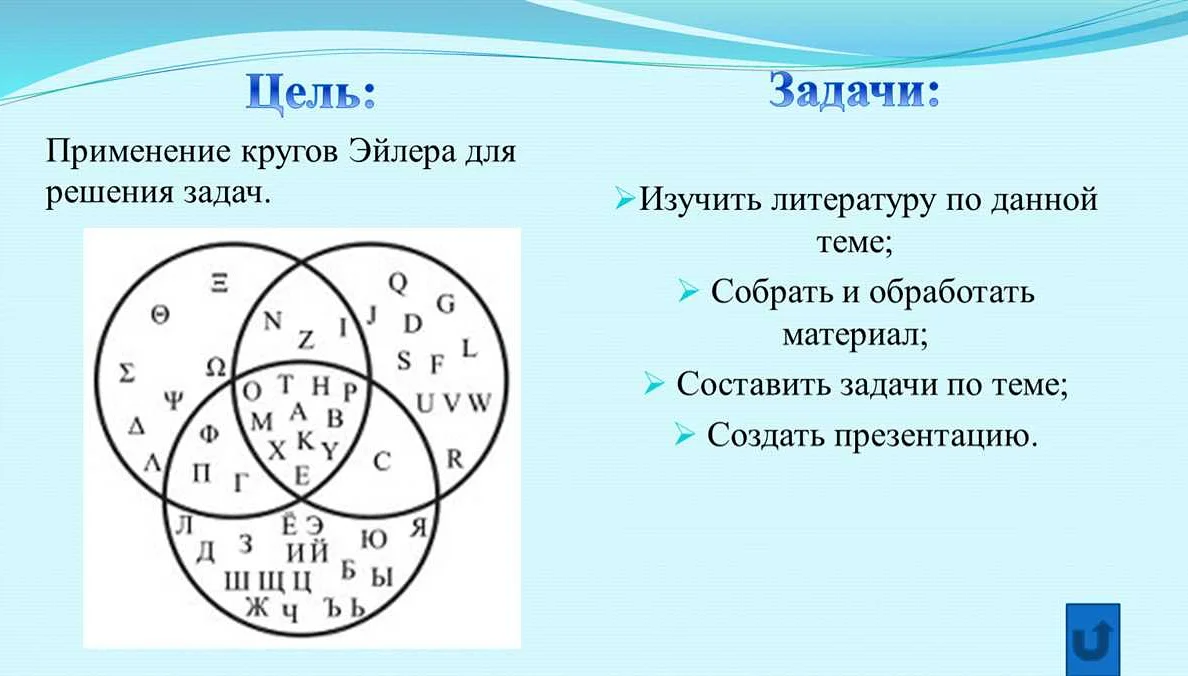
Основная идея кругов Эйлера заключается в изображении различных множеств и их пересечений в виде окружностей, которые пересекаются или не пересекаются друг с другом. Каждая окружность представляет отдельное множество, а пересечение окружностей показывает общие элементы двух или более множеств.

Круги Эйлера позволяют наглядно представить сложные отношения между множествами и их элементами. Они удобны для анализа объединений, пересечений, разности и подмножеств множеств. Круги Эйлера также помогают в построении логических диаграмм, принятии решений и решении задач с использованием формальной логики.

Применение кругов Эйлера может быть найдено в различных областях. Например, они используются в медицине и биологии для классификации и описания видов и их характеристик. В информационных технологиях они применяются для анализа баз данных и отношений между таблицами. В маркетинге круги Эйлера используются для анализа сегментации рынка и определения пересечений целевых аудиторий.

В заключение, круги Эйлера — это мощный инструмент для визуализации и анализа множеств и их отношений. Они помогают разбить сложные задачи на более простые и упрощают принятие решений. Понимание и применение кругов Эйлера полезно в различных областях и является важным навыком для математиков, ученых и аналитиков данных.

Определение и основные свойства

Основные свойства кругов Эйлера:

• Каждый круг представляет отдельное множество.
• Пересечение кругов показывает, что элементы принадлежат обоим множествам.
• Разность между кругами показывает элементы, которые принадлежат только одному множеству.
• Объединение всех кругов представляет собой объединение всех множеств.

Круги Эйлера позволяют наглядно представить сложные задачи по множествам и логическим операциям. Они также помогают визуализировать пересечения и различия между множествами.

Примеры задач, решаемых с помощью кругов Эйлера

Этот метод особенно полезен для решения задач на множествах, включающих элементы и подмножества. Круги Эйлера позволяют наглядно представить пересечения и объединения множеств, а также определить отношения между ними.

Рассмотрим несколько примеров задач, которые могут быть решены с помощью кругов Эйлера:

Пример 1: В классе 30 учеников. 15 из них занимаются футболом, 20 – играют в баскетбол. Сколько учеников занимаются и футболом, и баскетболом?

Для решения этой задачи можно использовать круги Эйлера. Нарисуем два круга – один для футболистов, другой для баскетболистов. Пересечение этих двух кругов покажет количество учеников, занимающихся и футболом, и баскетболом.

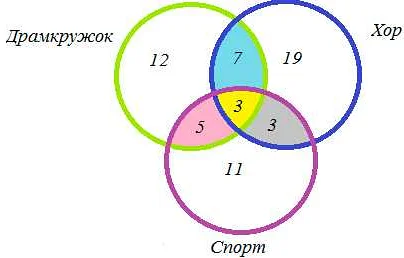
Пример 2: В магазине продается молоко, сыр и йогурт. 20% покупателей покупают только молоко, 30% покупают только сыр, а 10% покупают только йогурт. Сколько процентов покупателей покупают все три продукта?

Для решения этой задачи можно нарисовать три круга – для молока, сыра и йогурта. Пересечения этих кругов покажут процент покупателей, которые покупают все три продукта.

Пример 3: В городе 100 тысяч жителей. 40 тысяч жителей умеют плавать, 30 тысяч – умеют кататься на велосипеде, 20 тысяч – умеют играть на гитаре. Сколько жителей умеют плавать и кататься на велосипеде, но не умеют играть на гитаре?

Для решения этой задачи можно использовать круги Эйлера. Нарисуем три круга – для плавания, катания на велосипеде и игры на гитаре. Внешняя область, не пересекающая ни один из кругов, покажет количество жителей, которые умеют плавать и кататься на велосипеде, но не умеют играть на гитаре.

Таким образом, круги Эйлера представляют собой мощный графический инструмент для решения задач по математике, связанных с множествами и их отношениями. Они позволяют наглядно представить пересечения и взаимоотношения между различными множествами и помогают легко и точно решить задачу.

Методы решения задач с использованием кругов Эйлера

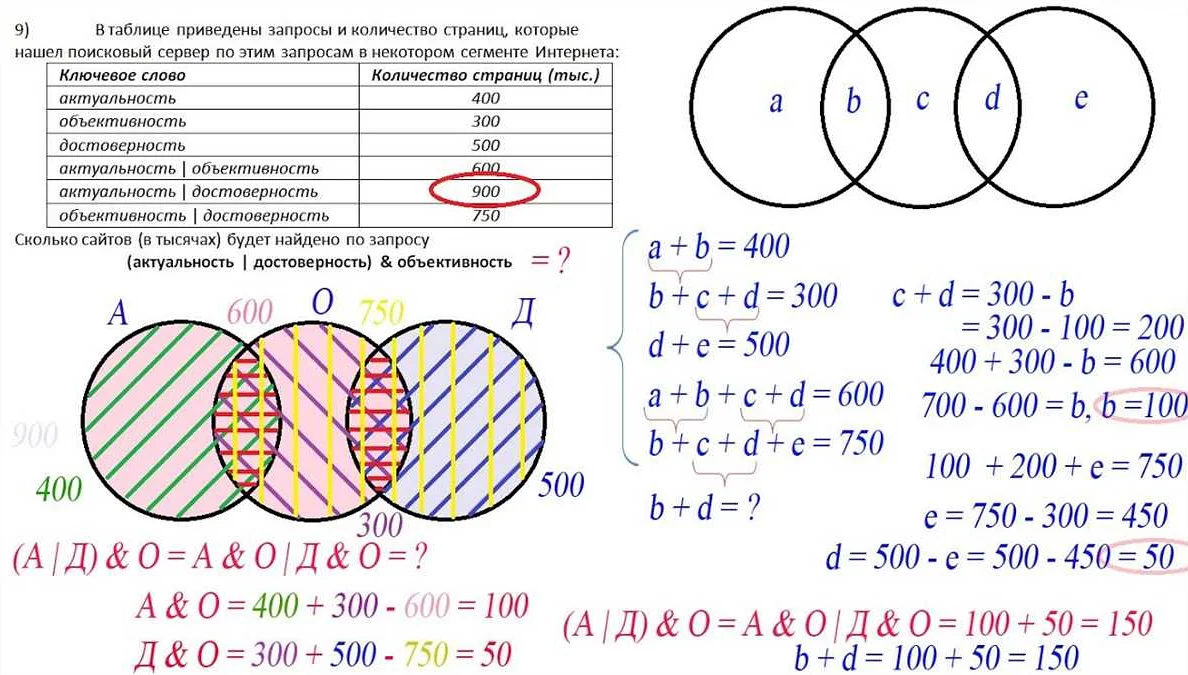
Метод основан на использовании специальных диаграмм, называемых кругами Эйлера, которые позволяют наглядно представить связи между множествами и выполнять операции с ними.

Основные операции, которые можно выполнять с помощью кругов Эйлера, включают:

• Объединение множеств: позволяет найти количество элементов, принадлежащих хотя бы одному из рассматриваемых множеств.
• Пересечение множеств: позволяет найти количество элементов, принадлежащих одновременно всем рассматриваемым множествам.
• Разность множеств: позволяет найти количество элементов, которые принадлежат одному множеству, но не принадлежат другому.

Для решения задач с использованием кругов Эйлера следует выполнить следующие шаги:

1. Нарисовать круги Эйлера, соответствующие рассматриваемым множествам, и заполнить их элементами.
2. Произвести необходимые операции над кругами, чтобы найти искомые значения.
3. Анализировать полученные результаты и делать выводы в соответствии с поставленной задачей.

Круги Эйлера являются удобным и эффективным инструментом для решения задач, связанных с множествами. Они позволяют наглядно представить информацию и легко выполнять операции над множествами. Использование кругов Эйлера может значительно упростить процесс решения задач и помочь получить точные и надежные результаты.

Метод включения-исключения

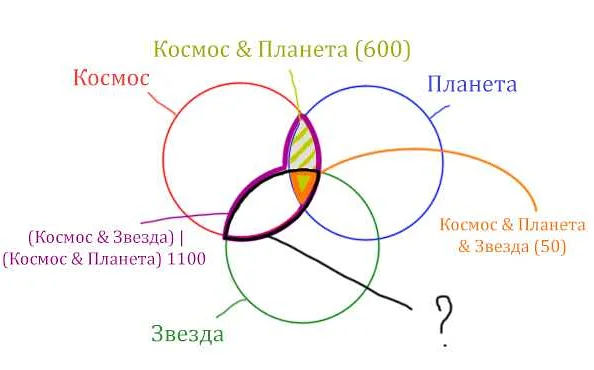
Для применения метода включения-исключения необходимо разбить задачу на подзадачи и выразить их через множества, используя операции объединения, пересечения и разности.

Основная идея метода заключается в следующем:

1. Включение: находим сумму мощностей каждого из подмножеств.

2. Исключение: вычитаем из этой суммы мощности каждого пересечения двух подмножеств.

3. Включение: прибавляем мощности каждого пересечения трех подмножеств.

4. Исключение: вычитаем мощности каждого пересечения четырех подмножеств.

И так далее, пока не пройдем по всем возможным комбинациям.

Применение метода включения-исключения позволяет разбить сложную задачу на более простые подзадачи и эффективно решить её, учитывая все возможные комбинации и исключая повторяющиеся элементы.

Одним из примеров применения метода включения-исключения является задача о раскраске графа: для решения этой задачи необходимо учесть все возможные цветовые комбинации, исключить повторяющиеся комбинации и определить минимальное количество цветов для раскраски графа.

Метод включения-исключения является мощным инструментом для решения задач по комбинаторике и теории вероятностей и находит применение в различных областях математики, экономики, информатики и других науках.

Метод решета

Для начала создается список чисел от 2 до заданного числа, которое хотим проверить на простоту. Затем мы начинаем с первого числа в списке (числа 2) и отмечаем все его кратные числа (числа, которые делятся на 2). После этого мы переходим к следующему нераскрашенному числу в списке (число 3) и отмечаем все его кратные числа. Процесс повторяется до тех пор, пока мы не достигнем конца списка.

В результате мы получаем список всех простых чисел до заданного числа. Этот метод эффективен, потому что мы не проверяем каждое число отдельно на простоту, а сразу отбрасываем множество составных чисел.

Программная реализация алгоритмов нахождения кругов Эйлера

Нахождение кругов Эйлера в графе может быть решено с помощью различных алгоритмов. При программной реализации этих алгоритмов необходимо учитывать особенности структуры данных и эффективность работы.

Один из наиболее распространенных алгоритмов для нахождения кругов Эйлера — алгоритм Флери. Он основывается на обходе графа с сохранением информации о пройденных ребрах. В процессе обхода алгоритм ищет эйлеров цикл, который является одним из кругов Эйлера. После нахождения эйлерова цикла, алгоритм ищет все другие циклы, которые не включены в эйлеров цикл, и объединяет их в круги Эйлера.

Для реализации алгоритма Флери необходимо использовать подходящую структуру данных, такую как граф или список смежности. Поэтому перед реализацией алгоритма необходимо представить граф в виде, удобном для работы с ним.

Еще одним алгоритмом для нахождения кругов Эйлера является алгоритм Хиршберга. Он основан на применении динамического программирования и позволяет находить все круги Эйлера в графе. Алгоритм Хиршберга эффективен при работе с большими графами, но требует дополнительных вычислительных ресурсов.

При реализации алгоритма Хиршберга также необходимо использовать подходящую структуру данных для представления графа и оптимизировать процесс вычислений.

Программная реализация алгоритмов нахождения кругов Эйлера требует глубокого понимания математической теории и алгоритмического подхода. При правильной реализации данных алгоритмов можно достичь высокой эффективности работы и точности результатов.

Важным аспектом программной реализации алгоритмов нахождения кругов Эйлера является их отладка и тестирование. Тщательное тестирование позволяет убедиться в корректности работы алгоритмов и их соответствии поставленным требованиям.

Выбор языка программирования и инструментов

При решении задач по математике с использованием Кругов Эйлера важно правильно выбрать язык программирования и инструменты для разработки. Это поможет повысить эффективность и удобство работы, а также обеспечить оптимальное использование ресурсов.

Один из ключевых факторов при выборе языка программирования — это его поддержка математических операций и алгоритмов. Некоторые языки, такие как Python, R или MATLAB, имеют встроенные функции для работы с математическими объектами, что упрощает разработку и ускоряет выполнение задач.

Важно также учесть специфические требования задачи. Если необходимо работать с большими объемами данных или выполнить сложные вычисления, то обращение к языкам программирования с высокой производительностью, например, C++ или Java, может быть предпочтительным. Эти языки позволяют эффективно использовать системные ресурсы и оптимизировать выполнение алгоритмов.

Помимо выбора языка программирования, также необходимо определиться с инструментами разработки. Например, будут использоваться интегрированные среды разработки (IDE) или текстовые редакторы. IDE обычно предоставляют более широкий набор функций, включая автозаполнение кода, отладку и удобную навигацию по проекту. Однако, для простых задач текстовые редакторы могут быть более легковесными и быстрыми в использовании.

Важным аспектом выбора инструментов является также их доступность и удобство использования. Некоторые языки программирования и инструменты имеют обширные сообщества разработчиков, что обеспечивает поддержку и быстрый доступ к ресурсам. Наличие документации, туториалов и примеров также может значительно облегчить процесс разработки и решения задач.

В итоге, выбор языка программирования и инструментов должен быть основан на требованиях конкретной задачи, а также наличии ресурсов и опыта разработчика. Важно учитывать особенности языка, его производительность, удобство использования и поддержку. Это поможет достичь максимальной эффективности и удобства при решении задач по математике с использованием Кругов Эйлера.

Вопрос-ответ:

Что такое круги Эйлера?

Круги Эйлера — это графический метод, позволяющий решать задачи по теории множеств. Он основан на использовании эйлеровых диаграмм, которые представляют собой пересекающиеся окружности, отображающие совокупности элементов множеств и их пересечения.

Как использовать круги Эйлера для решения математических задач?

Для решения задач с использованием кругов Эйлера необходимо сначала определить множества и их пересечения, а затем построить соответствующие эйлеровы диаграммы. Далее, используя правила эйлеровых диаграмм, можно выделить необходимые элементы и получить ответ на задачу.

Какие преимущества имеют круги Эйлера в сравнении с другими методами решения задач по математике?

Круги Эйлера обладают рядом преимуществ перед другими методами решения задач по математике. Они позволяют наглядно представить совокупности элементов множеств и их пересечения, что упрощает понимание задачи. Кроме того, круги Эйлера могут быть использованы не только для решения математических задач, но и для визуализации данных в других областях, таких как статистика и биология.

Можно ли использовать круги Эйлера для решения задач с большим количеством множеств?

Круги Эйлера могут быть использованы для решения задач с любым количеством множеств, однако их эффективность может снижаться при большом количестве элементов и пересечений. В таких случаях может быть полезно использовать другие методы, такие как матрицы или таблицы, для более удобного представления данных и решения задачи.

Какие сложности могут возникнуть при использовании кругов Эйлера для решения задач по математике?

При использовании кругов Эйлера для решения задач по математике могут возникнуть некоторые сложности. Например, сложно определить точные значения элементов множеств, если они представлены только в виде пересечений. Кроме того, при большом количестве элементов и пересечений может быть сложно сохранить наглядность и читаемость диаграммы. В таких случаях может потребоваться использование дополнительных инструментов, таких как цветовое обозначение или подписи, для удобства восприятия данных.

Примеры кода нахождения кругов Эйлера

Ниже приведены примеры кода на нескольких языках программирования для нахождения кругов Эйлера в графе:

Python:

def eulerian_circles(graph):
visited = set()
def dfs(v):
visited.add(v)
for u in graph[v]:
if u not in visited:
dfs(u)
eulerian_circles = []
for v in graph.keys():
dfs(v)
if len(visited) == len(graph):
eulerian_circles.append(v)
visited = set()
return eulerian_circles

Java:

import java.util.*;
public class EulerianCircles {
public static List<Integer> findEulerianCircles(Map<Integer, List<Integer>> graph) {
Set<Integer> visited = new HashSet<>();
void dfs(int v) {
visited.add(v);
for (int u : graph.get(v)) {
if (!visited.contains(u)) {
dfs(u);
}
}
}
List<Integer> eulerianCircles = new ArrayList<>();
for (int v : graph.keySet()) {
dfs(v);
if (visited.size() == graph.size()) {
eulerianCircles.add(v);
}
visited.clear();
}
return eulerianCircles;
}
}

C++:

#include <iostream>
#include <vector>
#include <unordered_set>
#include <unordered_map>
using namespace std;
vector<int> eulerianCircles(const unordered_map<int, vector<int>>& graph) {
unordered_set<int> visited;
void dfs(int v) {
visited.insert(v);
for (int u : graph.at(v)) {
if (visited.find(u) == visited.end()) {
dfs(u);
}
}
}
vector<int> eulerianCircles;
for (auto const&[v, _] : graph) {
dfs(v);
if (visited.size() == graph.size()) {
eulerianCircles.push_back(v);
}
visited.clear();
}
return eulerianCircles;
}
int main() {
unordered_map<int, vector<int>> graph = {
{1, {2, 3}},
{2, {1, 3}},
{3, {1, 2}}
};
vector<int> circles = eulerianCircles(graph);
for (int circle : circles) {
cout << circle << endl;
}
return 0;
}

Это лишь некоторые примеры кода нахождения кругов Эйлера. В зависимости от языка программирования и структуры данных, использованных для представления графа, код может отличаться.

Видео по теме: