Что такое остов дискретная математика

Остов дискретной математики — это подграф, полученный путем удаления нескольких ребер из заданного графа, при этом оставляя все вершины. Остов является связным подграфом и содержит все вершины исходного графа. Узнайте больше о понятии остова в дискретной математике и его применении.

Дискретная математика является одной из важнейших областей математики, изучающей дискретные объекты и структуры, такие как графы, комбинаторные структуры и логические системы. Одним из ключевых понятий в этой области является остов.

Остов графа – это подграф, содержащий все вершины исходного графа и некоторое подмножество его ребер. Остовы являются важным инструментом для изучения свойств графа и решения различных задач: поиска кратчайшего пути, построения оптимального дерева и многих других.

Одной из особенностей остовов является то, что они позволяют значительно упростить анализ графа, удалив избыточные ребра и сосредоточившись на наиболее важных связях.

Остовы активно применяются в различных областях, включая сетевые технологии, теорию кодирования, оптимизацию процессов и многие другие. Благодаря своей универсальности и простоте, они позволяют решать сложные задачи с минимальными затратами времени и ресурсов.

Определение остова

Остовом графа называется подграф, содержащий все вершины исходного графа, а также некоторое подмножество его ребер. В остове графа должно быть достаточно ребер, чтобы он оставался связным, но при этом не должно быть излишних ребер, которые могут быть удалены без нарушения связности графа.

Определение остова является одним из ключевых понятий в теории графов и находит широкое применение в различных областях, таких как транспортная логистика, компьютерные сети, маршрутизация и т. д.

Остовы графов используются для нахождения минимальных связных подграфов, которые содержат все вершины графа. Это позволяет оптимизировать использование ресурсов и улучшить эффективность различных алгоритмов, основанных на графовых структурах.

Свойства остовов

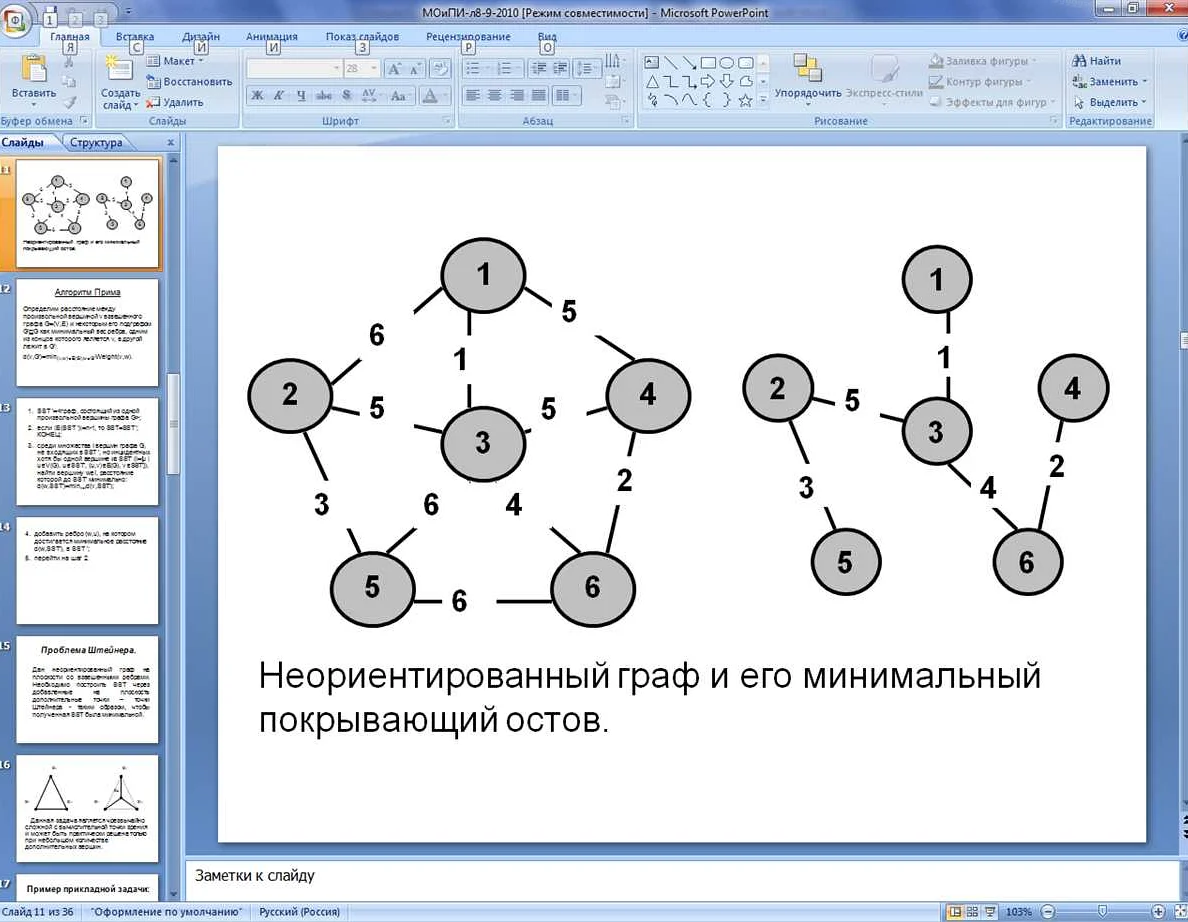
Свойства остовов:

1. Остов графа является подграфом исходного графа, то есть содержит его вершины и ребра.

2. Остов графа является связным графом, так как содержит все вершины исходного графа.

3. Остов графа имеет наименьшее возможное число ребер среди всех различных остовов данного графа. Если в остове удалить любое ребро, то граф перестанет быть связным.

4. Остов графа может быть не единственным, то есть граф может иметь несколько различных остовов.

5. Остов графа может содержать не все ребра исходного графа, но должен содержать достаточно ребер, чтобы быть связным.

6. Построение остова графа может быть полезным для решения различных задач, таких как оптимизация сетевых структур, минимальное остовное дерево и маршрутизация в компьютерных сетях.

Алгоритмы построения остовов

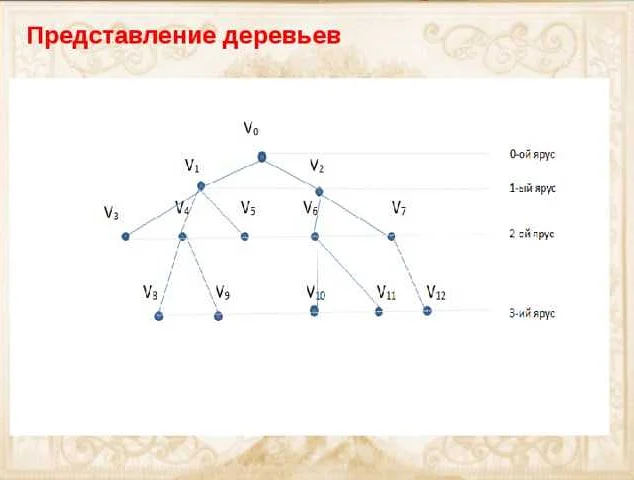
Остовом ориентированного или неориентированного графа называется его подграф, содержащий все вершины и некоторое подмножество ребер исходного графа, сохраняющий связность и не содержащий циклов.

Существует несколько алгоритмов для построения остовов:

1. Алгоритм Прима. Он начинает с некоторой начальной вершины и постепенно добавляет к остову новые ребра, соединяющие вершины уже имеющегося остова с вершинами, которые еще не входят в него. Процесс продолжается до тех пор, пока все вершины не будут включены в остов.

2. Алгоритм Краскала. Он строит остов на основе сортировки ребер по весу. Сначала все ребра сортируются по весу в неубывающем порядке. Затем алгоритм последовательно добавляет к остову ребра с наименьшим весом, при условии, что они не образуют цикл с уже добавленными ребрами.

3. Алгоритм Борувки. Он является модификацией алгоритма Краскала. Алгоритм последовательно строит компоненты связности графа и объединяет их, пока не останется единственная компонента, являющаяся остовом.

Алгоритмы построения остовов широко применяются в различных областях, таких как телекоммуникации, транспортная логистика, графовая оптимизация и другие. Они позволяют находить наименьшие остовы графов, которые могут использоваться для оптимизации сетей, маршрутизации и других задач.

Видео по теме:

Вопрос-ответ:

Что такое остов дискретной математики?

Остовом дискретной математики называется подграф, полученный из исходного графа путем удаления некоторых ребер. Остов содержит все вершины исходного графа и является связным, то есть между любыми двумя вершинами остова существует путь.

Какие особенности имеет остов дискретной математики?

Остов дискретной математики является связным подграфом, содержащим все вершины исходного графа. Остов имеет меньшее количество ребер, чем исходный граф, но при этом сохраняет связность между вершинами.

Зачем нужен остов в дискретной математике?

Остовы дискретной математики находят широкое применение в различных областях, таких как теория графов, сетевой анализ, оптимизация и др. Остовы позволяют упростить анализ графов и решение различных задач, таких как нахождение кратчайшего пути между вершинами или определение минимального остовного дерева.

Как вычислить остов дискретной математики?

Существует несколько алгоритмов для вычисления остовов дискретной математики, таких как алгоритм Прима, алгоритм Краскала и алгоритм Борувки. Все эти алгоритмы базируются на принципе «жадного выбора» и позволяют найти минимальный остов или остов, удовлетворяющий другим заданным условиям.

Какие задачи решаются с помощью остовов дискретной математики?

Остовы дискретной математики позволяют решать различные задачи, связанные с анализом графов. Например, с их помощью можно найти кратчайший путь между двумя вершинами, определить минимальное остовное дерево, найти цикл минимального веса и др. Остовы также применяются в сетевом анализе, чтобы оптимизировать распределение ресурсов и обеспечить эффективную передачу данных.

Что такое остов в дискретной математике?

Остовом графа называется его подграф, содержащий все вершины и некоторое подмножество ребер исходного графа, такое что остов остается связным, то есть между любыми двумя вершинами существует путь.

Какие особенности имеет остов в дискретной математике?

Остов графа может быть не единственным, так как можно удалить из него любое ребро и остов все равно останется связным. Остов может содержать некоторое подмножество ребер исходного графа или же быть полным, то есть содержать все ребра исходного графа. Остовы могут иметь различное количество ребер и вершин.

Применение остовов в дискретной математике

• Теория графов: Остовы помогают исследовать свойства графов и находить определенные пути и связи между вершинами. Они используются для анализа социальных сетей, транспортных систем, компьютерных сетей и других сложных структур.
• Кодирование и передача информации: Остовы применяются в теории кодирования и передачи информации для обнаружения ошибок и восстановления данных. Они позволяют найти минимальное покрытие вершинами и ребрами, что помогает обеспечить надежность и эффективность передачи информации.
• Алгоритмы и оптимизация: Остовы активно используются в алгоритмах для поиска минимального остовного дерева. Это помогает находить оптимальные пути и структуры в различных задачах, таких как коммивояжер, сетевой поток и маршрутизация.
• Системы безопасности и анализ рисков: Остовы применяются для выявления уязвимостей и анализа рисков в различных системах безопасности, таких как компьютерные сети, финансовые рынки и кибербезопасность. Они помогают определить наиболее критические точки и принять меры для предотвращения потенциальных угроз и атак.
• Математическое моделирование: Остовы используются для создания математических моделей сложных систем и их анализа. Они позволяют оценить важность и взаимодействие различных компонентов системы, что помогает принимать решения и оптимизировать процессы.

Применение остовов в дискретной математике весьма разнообразно и позволяет решать широкий спектр задач. Остовы являются одним из ключевых понятий в этой области и играют важную роль в анализе и оптимизации различных систем и структур.

Примеры использования остовов

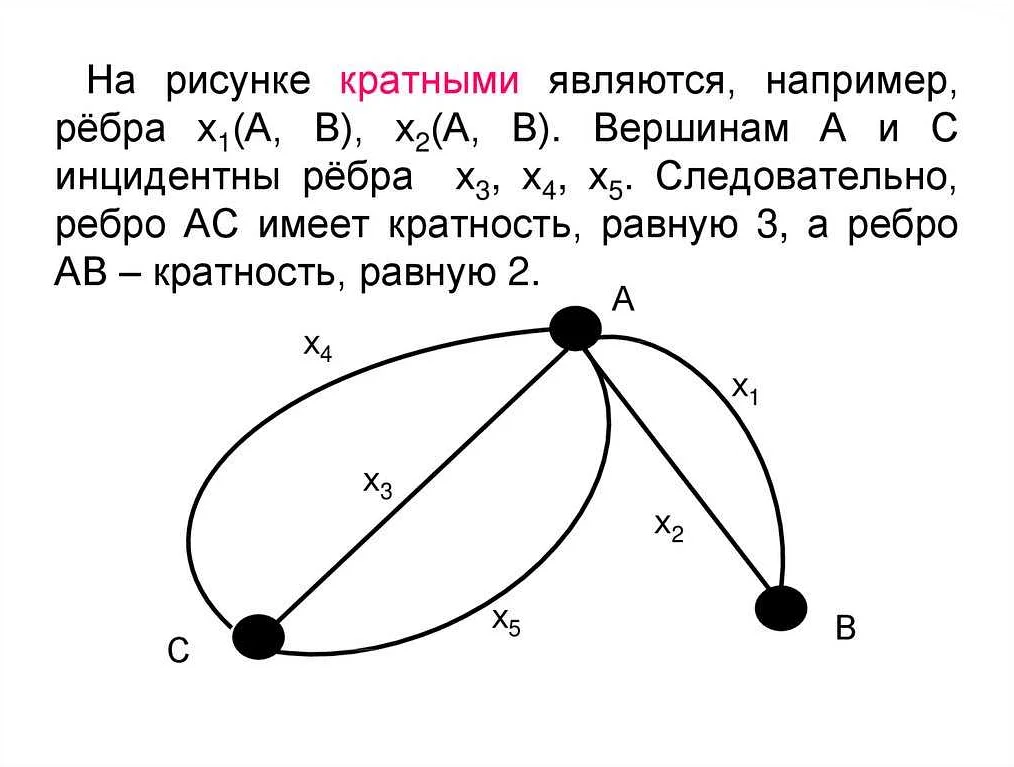
Остовы дискретных графов находят применение в различных областях, где важна связность и минимальность графа. Рассмотрим несколько примеров использования остовов:

ПримерОбласть применения

1	Телекоммуникации
2	Транспортная инфраструктура
3	Биоинформатика
4	Социальные сети

1. В телекоммуникациях остовы графов используются для оптимизации сетей. Они помогают выявить наиболее важные узлы и связи, обеспечивая стабильную передачу данных.

2. В транспортной инфраструктуре остовы графов помогают оптимизировать маршруты и улучшить эффективность транспортной системы. Они позволяют выявить наиболее важные дороги и пути сообщения.

3. В биоинформатике остовы графов используются для анализа генетических данных и выявления взаимосвязей между генами. Они помогают определить гены-маркеры и понять биологические процессы.

4. В социальных сетях остовы графов используются для анализа социальных связей и выявления ключевых акторов. Они помогают понять структуру сообществ и влияние отдельных пользователей.

Таким образом, остовы дискретных графов являются мощным инструментом для анализа и оптимизации различных систем. Они позволяют выявить наиболее важные элементы и связи, что является основой многих прикладных задач.