Круговые примеры математика 1 класс как решать

Узнайте, как решать круговые примеры в математике для первого класса. Научитесь использовать основные понятия, такие как радиус, диаметр и окружность, чтобы решать простые задачи. Получите полезные советы и стратегии для успешного решения круговых примеров.

Изучение математики в начальной школе является основой для понимания сложных концепций, которые будут встречаться детям в дальнейшем образовании. Одним из важных аспектов математики являются круговые примеры. Они не только помогают развить навыки счета и логического мышления, но и закладывают основы для дальнейших изучений геометрии.

Круговые примеры математики в 1 классе включают задачи, которые требуют от детей использования знаков операций (сложение, вычитание, умножение и деление) для решения проблем. Они также включают понятия о радиусе, диаметре и окружности. Дети должны уметь определить, какие из этих понятий применимы к конкретной задаче и как использовать их для решения.

Освоение правил решения круговых примеров математики в 1 классе требует понимания основных понятий и навыков счета. Дети должны быть знакомы с числами от 1 до 10, уметь складывать и вычитать числа до 10, а также понимать, что означают знаки операций. Для успешного освоения этих навыков необходимо практиковаться регулярно и использовать различные методы обучения, такие как игры и задачи на логическое мышление.

Как только дети освоят правила решения круговых примеров математики, они смогут применять эти навыки к решению более сложных задач. Это поможет им не только в математике, но и в других науках и повседневной жизни. Поэтому важно уделить достаточно времени и внимания изучению круговых примеров в начальной школе.

Основные понятия круговых примеров

Для правильного решения круговых примеров необходимо знать основные понятия, которые связаны с кругами. Вот некоторые из них:

• Длина окружности: это расстояние между двумя точками на окружности, которое проходит через центр окружности. Длину окружности обозначают буквой С.
• Радиус: это отрезок, соединяющий центр окружности с любой точкой на окружности. Радиус обозначается буквой R.
• Диаметр: это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Диаметр в два раза больше радиуса и обозначается буквой D.
• Площадь круга: это площадь, заключенная внутри окружности. Площадь круга обозначается буквой S.

Для решения круговых примеров нужно уметь применять формулы для нахождения длины окружности, площади круга, радиуса и диаметра. Также важно понимать, как связаны эти величины между собой.

При решении круговых примеров, необходимо учитывать, что значения радиуса, диаметра, длины окружности и площади круга могут быть даны в разных единицах измерения, например, в сантиметрах, метрах, дециметрах и т. д. Поэтому, при необходимости, нужно производить соответствующие преобразования.

Типы круговых примеров

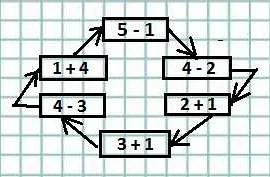
Существует несколько типов круговых примеров:

1. Нахождение длины окружности. В этом типе задач детям предлагается найти длину окружности по заданным данным, таким как радиус или диаметр круга.
2. Нахождение площади круга. В этом типе задач детям предлагается найти площадь круга по заданным данным, таким как радиус или диаметр круга.
3. Нахождение радиуса или диаметра круга. В этом типе задач детям предлагается найти радиус или диаметр круга по заданным данным, таким как длина окружности или площадь круга.
4. Решение задач на свойства круга. В этом типе задач детям предлагается использовать свойства круга для решения различных математических задач, таких как нахождение углов или длин отрезков.

Решение круговых примеров требует понимания основных правил и формул, связанных с кругом, а также умения применять их на практике. Постепенное освоение этих навыков поможет детям лучше понять геометрию и математику в целом.

Как решать примеры с кругами

Когда решаете примеры с кругами, необходимо использовать следующие правила:

1. Нахождение длины окружности:	Длина окружности вычисляется по формуле: L = 2 * π * r, где L – длина окружности, π – число Пи (примерно равно 3,14), r – радиус окружности.
2. Нахождение площади круга:	Площадь круга вычисляется по формуле: S = π * r^2, где S – площадь круга, π – число Пи, r – радиус окружности.
3. Решение задач, связанных с кругами:	Для решения задач, связанных с кругами, следует использовать знания о длине окружности и площади круга. Например, если известна длина окружности и требуется найти ее радиус, можно воспользоваться формулой L = 2 * π * r и выразить радиус r. Аналогично, если известна площадь круга и нужно найти его радиус, можно использовать формулу S = π * r^2 и выразить радиус r.

Правильное решение примеров с кругами требует внимательности и понимания основных правил и формул. С учетом этих знаний вы легко справитесь с заданиями, связанными с кругами, в математике 1 класса.

Правила выполнения круговых примеров

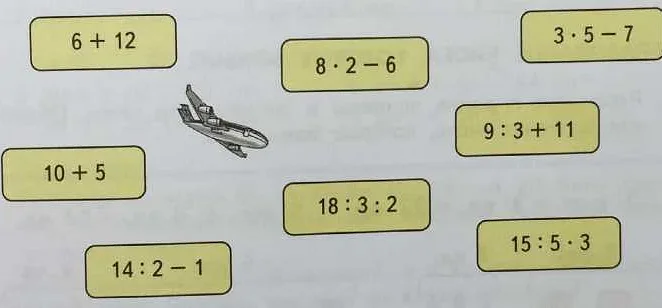
Круговые примеры в математике 1 класса представляют собой задачи, в которых необходимо найти значение неизвестного элемента в круговой диаграмме. Для успешного решения таких примеров, необходимо усвоить следующие правила:

1. Круговая диаграмма представляет собой круг, разделенный на секторы. Каждый сектор соответствует определенному значению или категории.

2. В круговом примере, один из секторов может быть неизвестным и обозначается буквой «х». Задача состоит в том, чтобы найти значение «х».

3. Для нахождения значения «х» необходимо использовать информацию, предоставленную в других секторах. Например, если известно, что сумма значений всех секторов равна 100%, можно использовать эту информацию для нахождения значения «х».

4. Для решения круговых примеров можно использовать различные математические операции, такие как сложение, вычитание, умножение и деление.

5. Важно внимательно анализировать предоставленные данные и правильно применять математические операции для нахождения значения «х».

6. После нахождения значения «х» необходимо проверить его правильность, используя предоставленные данные и математические операции.

7. Постоянная практика решения круговых примеров поможет улучшить навыки и повысить точность выполнения.

ПримерДаноРешение

Пример 1	В секторе «А» 30%, в секторе «В» 20%, в секторе «С» неизвестное значение «х». Сумма значений всех секторов равна 100%.	30% + 20% + «х» = 100% «х» = 100% — 30% — 20% «х» = 50%
Пример 2	В секторе «А» 40%, в секторе «В» неизвестное значение «х», в секторе «С» 10%. Сумма значений всех секторов равна 100%.	40% + «х» + 10% = 100% «х» = 100% — 40% — 10% «х» = 50%

Полезные советы по решению круговых примеров

Решение круговых примеров в математике может быть простым, если вы знаете правила и следуете нескольким полезным советам:

• Ознакомьтесь с основными терминами и определениями, связанными с кругами, такими как радиус, диаметр, окружность и центр.
• Помните, что радиус — это расстояние от центра круга до любой его точки, а диаметр — это отрезок, соединяющий две точки на окружности через ее центр.
• Узнайте формулы для вычисления длины окружности и площади круга. Эти формулы могут помочь вам решать задачи, связанные с кругами.
• Если вам дана площадь круга или длина окружности, используйте соответствующую формулу, чтобы найти радиус или диаметр.
• Если вам даны радиус или диаметр, используйте соответствующую формулу, чтобы найти площадь круга или длину окружности.
• При решении задач с круговыми примерами обратите внимание на единицы измерения. Убедитесь, что вы используете правильные единицы и правильно округляете результаты.
• Не забывайте проверять свои ответы, решая задачи с помощью различных методов. Это поможет вам увериться, что вы правильно понимаете и применяете правила для решения круговых примеров.

Следуя этим полезным советам, вы сможете успешно решать круговые примеры и легко освоить правила математики.

Примеры решения круговых задач

Круговые задачи в математике требуют знания основных правил и формул, связанных с окружностями. Рассмотрим несколько примеров решения круговых задач:

Пример 1: Дана окружность с радиусом 5 см. Найдите длину окружности. Решение: Длина окружности вычисляется по формуле L = 2πr, где L — длина окружности, π — число Пи (приближенно равно 3,14), r — радиус окружности. Подставляем известные значения в формулу: L = 2 * 3,14 * 5 = 31,4 см.

Пример 2: Дана окружность с диаметром 12 см. Найдите площадь круга, описанного около этой окружности. Решение: Площадь круга вычисляется по формуле S = πr^2, где S — площадь круга, π — число Пи (приближенно равно 3,14), r — радиус окружности. Так как диаметр окружности равен 12 см, то радиус будет равен половине диаметра, то есть 12 / 2 = 6 см. Подставляем известные значения в формулу: S = 3,14 * 6^2 = 113,04 см^2.

Пример 3: Дана окружность с радиусом 8 см. Найдите площадь сектора, если центральный угол составляет 60 градусов. Решение: Площадь сектора вычисляется по формуле S = (πr^2 * α) / 360, где S — площадь сектора, π — число Пи (приближенно равно 3,14), r — радиус окружности, α — центральный угол в градусах. Подставляем известные значения в формулу: S = (3,14 * 8^2 * 60) / 360 = 33,47 см^2.

Таким образом, знание основных правил и формул позволяет решать круговые задачи в математике. При решении задач важно внимательно читать условия, правильно применять формулы и проводить вычисления.

Тренировка и контрольные задания по круговым примерам

Для освоения правил решения круговых примеров в математике 1 класса необходимо проводить регулярную тренировку и выполнять контрольные задания. Только так можно закрепить полученные знания и умения.

Во время тренировки по круговым примерам рекомендуется использовать различные материалы, такие как учебники, рабочие тетради, интерактивные задачники и приложения. Важно разнообразить подходы к решению задач, чтобы ученик мог научиться применять различные стратегии и методы.

Контрольные задания позволяют оценить уровень усвоения материала и выявить пробелы в знаниях. Они могут быть представлены в форме тестовых заданий, задач на применение правил или задач на доказательство. Контрольные задания помогут ученику узнать, насколько хорошо он усвоил правила и умеет применять их на практике.

Для эффективной тренировки и выполнения контрольных заданий необходимо соблюдать следующие рекомендации:

1. Постепенно увеличивать сложность заданий, начиная с простых и постепенно переходя к более сложным.
2. Проводить тренировку и выполнение заданий регулярно, чтобы не терять навыки.
3. Обращать внимание на ошибки и искать способы их исправления. Разбирать с учеником ошибочные решения и объяснять, как правильно решать задачи.
4. Стимулировать ученика к самостоятельности и поощрять его за успешное выполнение заданий.

Тренировка и контрольные задания по круговым примерам помогут ученику закрепить и усовершенствовать полученные знания и навыки. Регулярные тренировки и выполнение задач помогут ученику стать уверенным в решении круговых примеров и успешно продолжать изучение математики.

Вопрос-ответ:

Какие примеры можно использовать для освоения кругов?

Для освоения кругов можно использовать различные примеры, такие как: нарисовать круг с заданным радиусом, найти длину окружности, найти площадь круга и т.д.

Как решать задачу на нахождение площади круга?

Для нахождения площади круга нужно умножить квадрат радиуса на число Пи (π). Формула для расчета площади круга: S = π * r^2, где S — площадь круга, r — радиус.

Как найти длину окружности?

Длина окружности можно найти по формуле L = 2 * π * r, где L — длина окружности, r — радиус. Нужно умножить диаметр окружности на число Пи (π).

Как решать задачу на нахождение радиуса круга?

Для нахождения радиуса круга, если известна длина окружности, нужно использовать формулу r = L / (2 * π), где r — радиус, L — длина окружности.

Какие еще правила есть для работы с кругами?

Помимо нахождения площади и длины окружности, с кругами можно работать с помощью правил: находить радиус по диаметру, находить диаметр по радиусу, находить площадь сектора круга и т.д.

Игры и задания для закрепления круговых примеров

Для того чтобы лучше запомнить и освоить правила решения круговых примеров, можно использовать различные игры и задания. Это поможет учащимся лучше понять материал и применять его на практике.

Одна из игр, которую можно провести на уроке, — «Кто быстрее». Учитель задает круговые примеры, а ученики должны решить их как можно быстрее. Победителем будет тот, кто первым правильно решит большинство примеров.

Другая игра — «Заполни пропуски». Учитель записывает несколько круговых примеров на доске, но оставляет пропуски в некоторых местах. Ученики должны правильно заполнить пропуски, используя правила решения круговых примеров. Такая игра поможет учащимся лучше запомнить и применять правила.

Еще одно задание — «Выбери правильный ответ». Учитель задает вопросы, касающиеся круговых примеров, и предлагает несколько вариантов ответов. Ученики должны выбрать правильный ответ. Такое задание поможет учащимся проверить свои знания и закрепить правила решения круговых примеров.

Видео по теме: