Круговые примеры что это 2 класс математика

Круговые примеры в математике для второго класса: что это такое, как их решать и зачем нужны. Узнайте, как решать задания с круговыми примерами и улучшите навыки своего ребенка в математике.

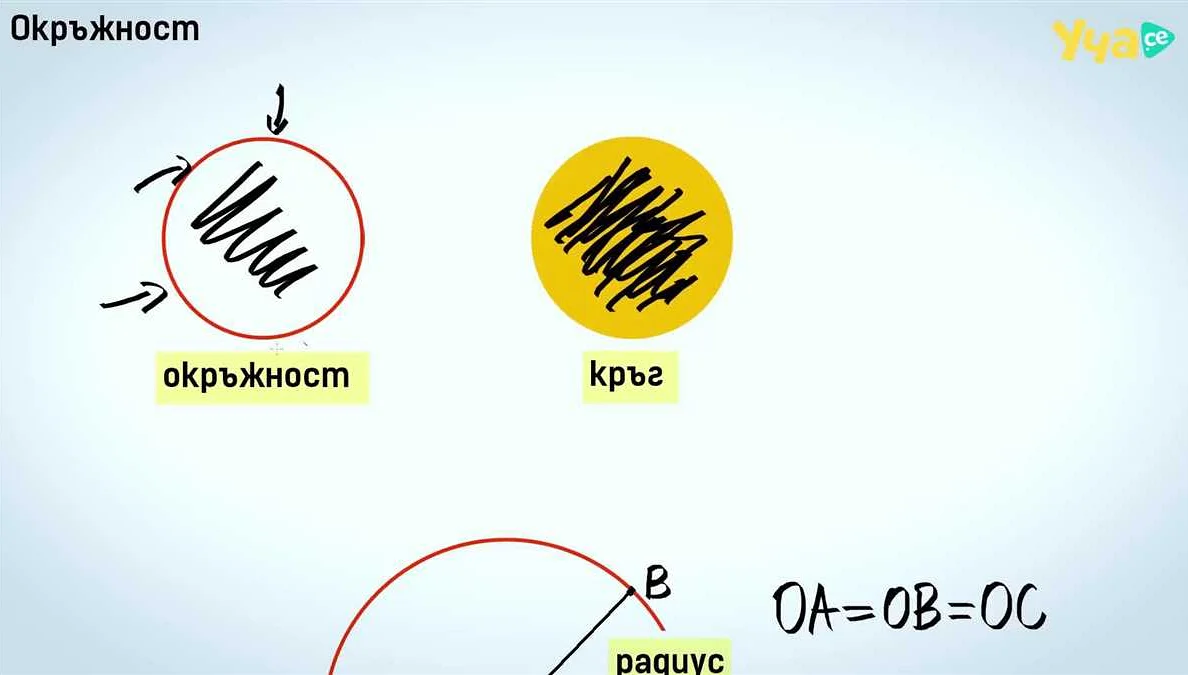
Математика является одним из главных предметов в школе, и круговые примеры играют важную роль в ее изучении. Круговые примеры помогают детям понять основные понятия геометрии, такие как радиус, диаметр и окружность.

Радиус — это линия, идущая от центра окружности до ее края. Диаметр — это линия, проходящая через центр окружности и соединяющая две ее точки. Окружность — это геометрическое место всех точек, находящихся на одинаковом расстоянии от центра.

Круговые примеры помогают детям понять взаимосвязь между этими понятиями. Например, чтобы найти длину окружности, нужно знать ее радиус или диаметр. Формула для расчета длины окружности — это 2πr, где r — радиус окружности.

Пример: если радиус окружности равен 5 см, то длина окружности будет 2 × 3.14 × 5 = 31.4 см.

Круговые примеры не только помогают детям развивать навыки решения задач, но и позволяют им увидеть, как математика применяется в реальной жизни. Например, круговые примеры могут быть использованы для измерения длины тела или объема контейнера.

Что такое круговые примеры в математике?

В круговых примерах ученикам могут предлагаться задачи на нахождение длины окружности, радиуса или диаметра круга, а также задачи, связанные с площадью круга. Они могут содержать вопросы о взаимосвязи между различными элементами круга и о применении этих понятий на практике.

Круговые примеры могут быть представлены в различных форматах: в виде текстовых задач, иллюстраций или графиков. Они могут быть как простыми, так и сложными, в зависимости от уровня подготовки и возраста учащихся.

Решение круговых примеров требует применения математических формул и правил, а также логического мышления. Ученикам необходимо уметь анализировать задачу, определять известные и неизвестные переменные, использовать соответствующие формулы и выполнять необходимые вычисления.

Круговые примеры помогают развивать не только математические навыки, но и умение применять полученные знания на практике. Они могут быть интересными и захватывающими для учеников, поскольку позволяют им увидеть практическое применение математики в реальной жизни.

Определение и объяснение

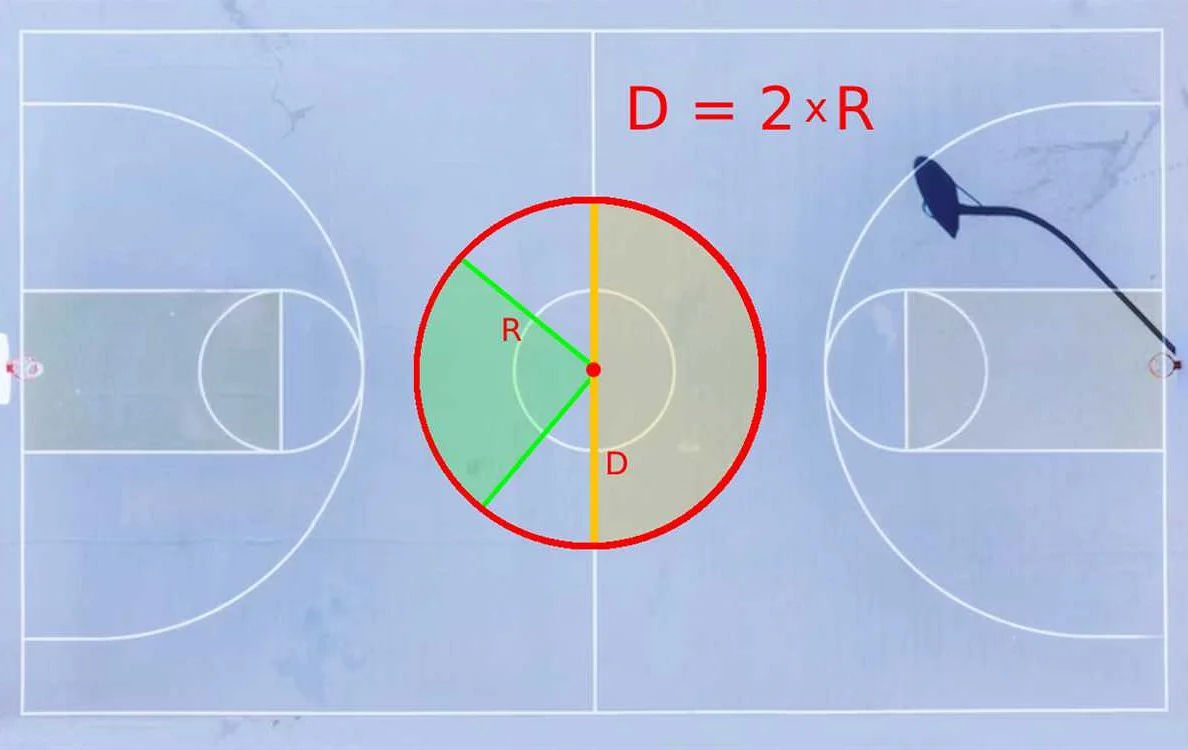
Радиус круга — это отрезок, соединяющий центр круга с любой точкой на его окружности. Диаметр круга — это отрезок, соединяющий две точки на окружности, проходящие через его центр. Диаметр всегда равен удвоенному радиусу.

Круг может быть использован для изучения различных математических понятий и задач, таких как измерение длины окружности, вычисление площади круга, а также для решения задач на нахождение периметра и площади фигур, основанных на круге.

Круговые примеры для 2 класса помогают детям понять основные концепции, связанные с кругом, и развивают их математические навыки. Они могут включать задачи на определение радиуса и диаметра круга, нахождение длины окружности, вычисление площади круга и другие задачи, требующие использования знаний о круге и его свойствах.

ТерминОпределение

Круг	Геометрическая фигура, которая состоит из всех точек на плоскости, расстояние от которых до центра круга равно его радиусу.
Радиус	Отрезок, соединяющий центр круга с любой точкой на его окружности.
Диаметр	Отрезок, соединяющий две точки на окружности круга, проходящие через его центр. Диаметр всегда равен удвоенному радиусу.

Зачем изучать круговые примеры во 2 классе?

Знание круговых примеров позволяет детям:

• Понимать основные элементы круга, такие как радиус, диаметр и окружность;
• Уметь измерять длину окружности и площадь круга;
• Решать задачи, связанные с круговыми примерами, например, находить длину окружности, если известен радиус.

Изучение круговых примеров во 2 классе также способствует развитию математического мышления у детей. Они учатся анализировать геометрические фигуры, решать проблемы и применять математические навыки на практике.

Важно отметить, что изучение круговых примеров имеет практическое применение в реальной жизни. Знания о круге и его элементах могут пригодиться при работе с круглыми предметами, такими как тарелки, колеса и монеты. Понимание круговых примеров также помогает учащимся в более сложных математических темах, таких как геометрия и тригонометрия.

В итоге, изучение круговых примеров во 2 классе имеет значительное значение для развития математического мышления, формирования представления о геометрических фигурах и подготовки учащихся к более сложным математическим темам в будущем.

Примеры круговых примеров

В математике существует несколько типов задач, связанных с кругами. Вот несколько примеров круговых задач, которые помогут вам лучше понять эту тему:

№ПримерРешение

1	Найдите площадь круга с радиусом 5 см.	Формула для площади круга: S = π * r^2. Подставляем значение радиуса: S = 3.14 * 5^2 = 3.14 * 25 = 78.5 см^2. Ответ: 78.5 см^2.
2	Найдите длину окружности с радиусом 8 м.	Формула для длины окружности: L = 2 * π * r. Подставляем значение радиуса: L = 2 * 3.14 * 8 = 50.24 м. Ответ: 50.24 м.
3	У Анны есть круглый торт диаметром 20 см. Она хочет разделить его на 8 равных частей. Какой будет площадь каждой части?	Сначала находим радиус круга: r = d / 2 = 20 / 2 = 10 см. Затем находим площадь круга: S = π * r^2 = 3.14 * 10^2 = 3.14 * 100 = 314 см^2. Делим площадь на количество частей: 314 / 8 = 39.25 см^2. Ответ: 39.25 см^2.

Это лишь некоторые из множества задач, связанных с кругами. Решая такие примеры, вы сможете лучше понять основные понятия и формулы, связанные с кругами, и применять их на практике.

Как решать круговые примеры?

Решение круговых примеров в математике для 2 класса основывается на знании основных понятий, связанных с кругом. При решении таких примеров необходимо учитывать следующие факты:

1. Радиус круга — это отрезок, соединяющий центр круга с любой точкой его окружности.
2. Диаметр круга — это отрезок, соединяющий две точки окружности и проходящий через его центр. Диаметр равен удвоенному значению радиуса.
3. Площадь круга — это количество площади, заключенной внутри его границы. Формула для вычисления площади круга: S = π * r^2, где S — площадь, π — математическая константа (приближенное значение 3,14), r — радиус круга.
4. Длина окружности — это длина границы круга. Формула для вычисления длины окружности: C = 2 * π * r, где C — длина окружности, π — математическая константа (приближенное значение 3,14), r — радиус круга.

Чтобы решить круговой пример, необходимо определить, какая информация известна, и что требуется найти. Затем можно использовать соответствующую формулу для вычисления искомой величины.

Например, если известен радиус круга и требуется найти его площадь, можно воспользоваться формулой для вычисления площади круга: S = π * r^2. Подставив известные значения, можно найти искомую площадь.

Важно помнить, что при решении круговых примеров необходимо учитывать единицы измерения, которые используются. Например, если радиус круга задан в сантиметрах, то и площадь будет выражена в квадратных сантиметрах.

Решая круговые примеры и изучая свойства круга, ученик развивает навыки логического мышления, а также способность применять математические знания на практике.

Развитие логического мышления через круговые примеры

Круговые примеры представляют собой задания, в которых детям предлагается рассмотреть различные объекты или явления, связанные с кругом. Например, они могут анализировать, какие предметы имеют форму круга, составлять списки или классифицировать их по разным признакам.

Такие задания помогают детям улучшить свою концентрацию, внимательность и способность к классификации и организации информации. Они учат детей различать геометрические формы, анализировать объекты и давать им определенные характеристики.

Круговые примеры также помогают развивать математические навыки у детей. Например, дети могут считать количество круговых предметов, сравнивать их размеры или находить различные способы комбинирования таких предметов.

Важно отметить, что круговые примеры могут быть представлены в различных форматах, таких как задачи, игры или головоломки. Это позволяет детям находить интересные и разнообразные способы решения заданий и развивать свою креативность.

Использование круговых примеров в обучении помогает детям не только развивать свое логическое мышление, но и улучшает их общую учебную мотивацию и интерес к изучению математики. Они становятся более уверенными в своих способностях и готовыми к новым трудностям и вызовам.

В итоге, использование круговых примеров в обучении помогает детям развивать логическое мышление, математические навыки и общую учебную мотивацию. Они учатся анализировать, делать выводы и применять полученные знания в реальной жизни.

Видео по теме:

Вопрос-ответ:

Зачем нужен круг в математике?

Круг в математике — это геометрическая фигура, которая имеет множество применений. Например, круг используется для изучения геометрических свойств, таких как диаметр, радиус, длина окружности и площадь. Он также играет важную роль в изучении углов, дуг и секторов. Круговые примеры помогают ученикам лучше понять эти концепции и применять их на практике.

Как можно объяснить диаметр круга детям 2 класса?

Диаметр круга — это отрезок, который проходит через центр круга и соединяет две противоположные точки на его окружности. Если представить, что круг это пирог, то диаметр — это линия, которую нужно провести от центра пирога до его края. Диаметр также является двойной длиной радиуса, то есть если радиус равен 5 сантиметров, то диаметр будет равен 10 сантиметрам.

Как вычислить длину окружности, если известен ее радиус?

Длину окружности можно вычислить по формуле: L = 2 * π * r, где L — длина окружности, π примерно равно 3,14, а r — радиус окружности. Если, например, радиус равен 4 сантиметрам, то длина окружности будет равна примерно 25,12 сантиметра. Эта формула помогает нам рассчитать длину окружности, зная только радиус, без необходимости измерять каждый отрезок.

Как найти площадь сектора круга?

Чтобы найти площадь сектора круга, нужно использовать формулу: S = (θ/360) * π * r^2, где S — площадь сектора, θ — центральный угол в градусах, π примерно равно 3,14, а r — радиус круга. Например, если центральный угол сектора равен 60 градусам, а радиус равен 7 сантиметрам, то площадь сектора будет равна примерно 22,99 квадратных сантиметра.

Какие примеры круговых задач можно использовать для объяснения во втором классе?

Во втором классе можно использовать примеры, связанные с изучением окружностей и их свойств. Например, можно показать детям разные объекты, имеющие форму окружности, и попросить их указать на эти объекты. Также можно задать вопросы о том, какие предметы можно нарисовать, используя только окружность, или попросить детей нарисовать разные окружности разного размера.

Как можно объяснить детям, что такое радиус и диаметр окружности?

Одним из способов объяснить детям, что такое радиус и диаметр окружности, является использование конкретных предметов. Например, можно взять разные круглые предметы разного размера, например, тарелку и крышку от банки, и показать детям, что радиус — это расстояние от центра окружности до ее края, а диаметр — это расстояние, проходящее через центр окружности и соединяющее противоположные края. Также можно использовать рисунки и схемы, чтобы наглядно показать разницу между радиусом и диаметром.

Практическое применение круговых примеров в жизни

Круговые примеры в математике не только помогают ученикам понять основные понятия о круге, но и имеют практическое применение в жизни. Рассмотрим несколько примеров:

ПримерПрактическое применение

Вычисление длины окружности	Знание формулы для вычисления длины окружности позволяет решать задачи, связанные с измерением и построением круговых объектов. Например, при изготовлении колес для транспортных средств необходимо знать длину окружности, чтобы правильно подобрать размер шины.
Вычисление площади круга	Знание формулы для вычисления площади круга помогает в решении задач, связанных с площадью круговых поверхностей. Например, при покраске стены, имеющей форму полукруга, нужно знать площадь этой поверхности, чтобы правильно рассчитать количество краски.
Измерение углов	Знание понятия радиана и его связи с градусами позволяет измерять и описывать углы не только в математике, но и в других областях. Например, в архитектуре и строительстве углы измеряются в градусах и радианах для точного позиционирования строительных элементов.

Таким образом, знание и понимание круговых примеров в математике имеет практическое применение в различных сферах нашей жизни.

Подготовка круговых примеров для домашнего задания

Перед тем как приступить к составлению примеров, необходимо убедиться в том, что ученики понимают основные понятия, такие как радиус, диаметр и окружность. Эти понятия могут быть объяснены с помощью наглядных материалов, таких как модели кругов и геометрических фигур.

После того, как ученики освоили основные понятия, можно приступать к формированию круговых примеров. Примеры могут быть различных типов: находить периметр круга, находить площадь круга, находить длину дуги, находить радиус или диаметр круга и т. д.

Важно учитывать, что примеры должны быть разнообразными и интересными для учеников. Также необходимо учитывать уровень подготовки каждого ученика и предлагать задания, соответствующие его знаниям и умениям.

Для того чтобы ученики могли успешно выполнить домашнее задание, необходимо предоставить им достаточное количество времени на его выполнение. Также можно предложить дополнительные материалы и задания для самостоятельной работы.

Важно помнить, что круговые примеры являются важной частью изучения математики и помогают развивать у учеников логическое мышление, творческое мышление и аналитические способности.

Таким образом, подготовка круговых примеров для домашнего задания требует тщательного планирования и организации. Необходимо учитывать основные понятия, уровень подготовки учеников и предоставить им достаточно времени и материалов для успешного выполнения задания.