Что такое площадь квадрата 2 класс правило математика

Площадь квадрата — это мера площади, которая выражает, сколько единиц площади может поместиться внутри квадрата. Правило площади квадрата для учеников 2 класса в математике.

Площадь — величина, которая характеризует размер поверхности фигуры. Одна из самых простых фигур, площадь которой можно вычислить, это квадрат. Квадрат — это четырехугольник, все стороны которого равны друг другу. У каждого квадрата есть своя площадь, которую можно выразить численным значением.

Во втором классе школы дети изучают правило для вычисления площади квадрата. Оно очень простое: площадь квадрата равна квадрату длины его стороны Другими словами, чтобы найти площадь квадрата, нужно умножить длину одной его стороны на саму себя. Например, если сторона квадрата равна 5 см, то его площадь будет 5 см * 5 см = 25 см².

Особенностью вычисления площади квадрата является то, что она измеряется в квадратных единицах. Например, если сторона квадрата измеряется в сантиметрах, то площадь будет измеряться в квадратных сантиметрах (см²). Это важно помнить при решении задач и записи ответов.

Определение площади квадрата

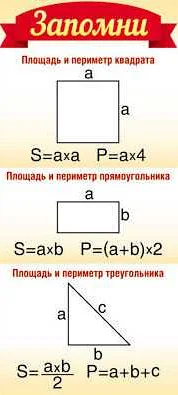
Площадь квадрата можно вычислить, зная длину его стороны. Для этого необходимо умножить длину стороны на саму себя, то есть возвести ее в квадрат. Формула для вычисления площади квадрата выглядит следующим образом:

S = a × a

где S — площадь квадрата, а — длина стороны.

Например, если сторона квадрата равна 5, то его площадь будет:

S = 5 × 5 = 25

Таким образом, площадь квадрата со стороной 5 равна 25 квадратным единицам.

Как вычислить площадь квадрата

Площадь квадрата можно вычислить, зная длину одной из его сторон. Для этого необходимо возвести длину стороны в квадрат, то есть умножить ее на саму себя.

Формула для вычисления площади квадрата:

S = a2

Где:

• S — площадь квадрата;
• a — длина стороны квадрата.

Например, если длина стороны квадрата равна 5 см, то его площадь будет:

S = 52 = 25 см2

Таким образом, площадь квадрата можно вычислить, зная длину одной из его сторон и применив формулу S = a2.

Формула площади квадрата

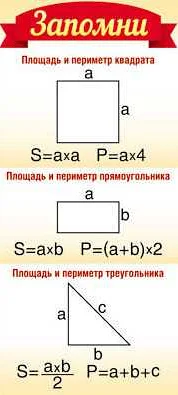
Площадь квадрата вычисляется по простой формуле: площадь равна квадрату длины стороны квадрата.

Формула площади квадрата записывается следующим образом:

П = a²

Где:

• П — площадь квадрата
• a — длина стороны квадрата

Для расчета площади квадрата нужно знать только длину одной его стороны. Поэтому, если известна длина стороны квадрата, достаточно возвести ее в квадрат, чтобы получить площадь.

Например, если сторона квадрата равна 5 сантиметров, то его площадь будет равна 5² = 25 сантиметров квадратных.

Примеры вычисления площади квадрата

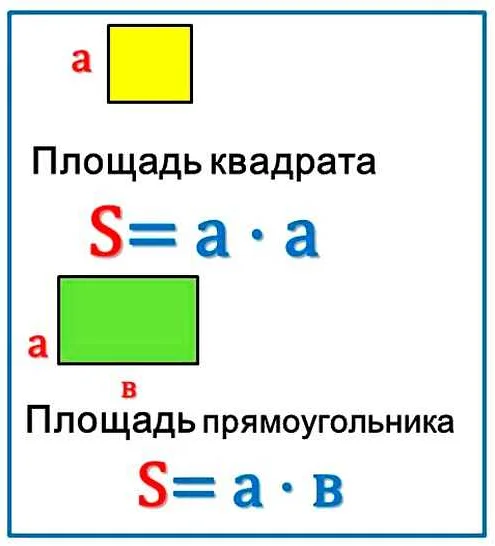
Рассмотрим несколько примеров вычисления площади квадрата по его стороне.

Пример 1:

Пусть сторона квадрата равна 5 см. Тогда площадь квадрата можно вычислить по формуле: Площадь = сторона * сторона. Подставим в формулу значение стороны: площадь = 5 см * 5 см = 25 см2. Таким образом, площадь квадрата равна 25 квадратным сантиметрам.

Пример 2:

Пусть сторона квадрата равна 8 см. Тогда площадь квадрата можно вычислить по формуле: Площадь = сторона * сторона. Подставим в формулу значение стороны: площадь = 8 см * 8 см = 64 см2. Таким образом, площадь квадрата равна 64 квадратным сантиметрам.

Пример 3:

Пусть сторона квадрата равна 10 см. Тогда площадь квадрата можно вычислить по формуле: Площадь = сторона * сторона. Подставим в формулу значение стороны: площадь = 10 см * 10 см = 100 см2. Таким образом, площадь квадрата равна 100 квадратным сантиметрам.

И таким образом, площадь квадрата можно вычислить, умножив значение его стороны на саму себя.

Свойства площади квадрата

Свойства площади квадрата:

• Площадь квадрата равна произведению длины его стороны на саму себя. Если сторона квадрата равна a, то площадь равна S = a × a или S = a².
• Все стороны квадрата равны между собой.
• Все углы квадрата прямые.
• Диагонали квадрата равны между собой и являются взаимно перпендикулярными. Длина диагонали можно найти с помощью теоремы Пифагора: d = a√2, где d — длина диагонали, а a — длина стороны квадрата.

Свойства площади квадрата очень полезны при решении задач на нахождение площади фигуры или нахождение длины стороны квадрата.

Единицы измерения площади квадрата

Площадь квадрата измеряется в квадратных единицах, которые обозначаются как кв. ед.

Наиболее распространенными единицами измерения площади квадрата являются:

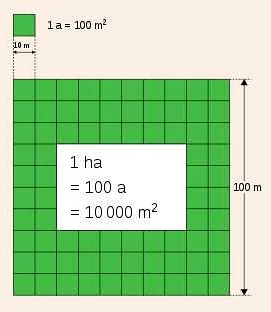
• Квадратный метр (м2)
• Квадратный сантиметр (см2)
• Квадратный дециметр (дм2)
• Квадратный миллиметр (мм2)

Квадратный метр (м2) является основной единицей измерения площади в СИ (Системе Международных единиц). Он равен площади квадрата со стороной в 1 метр.

Квадратный сантиметр (см2) является наиболее распространенной единицей измерения площади в повседневной жизни. Он равен площади квадрата со стороной в 1 сантиметр.

Квадратный дециметр (дм2) является единицей измерения площади, которая используется в некоторых странах. Он равен площади квадрата со стороной в 1 дециметр.

Квадратный миллиметр (мм2) является меньшей единицей измерения площади. Он равен площади квадрата со стороной в 1 миллиметр.

Знание единиц измерения площади квадрата позволяет корректно проводить измерения и сравнивать площади разных объектов.

Видео по теме:

Вопрос-ответ:

Как вычислить площадь квадрата?

Площадь квадрата вычисляется по формуле: сторона квадрата возводится в квадрат. Например, если сторона квадрата равна 5 см, то его площадь будет равна 25 квадратных сантиметров.

Какие особенности имеет площадь квадрата?

Особенностью площади квадрата является равенство площади всех его сторон. Это означает, что если сторона квадрата равна 5 см, то его площадь будет равна 25 квадратных сантиметров.

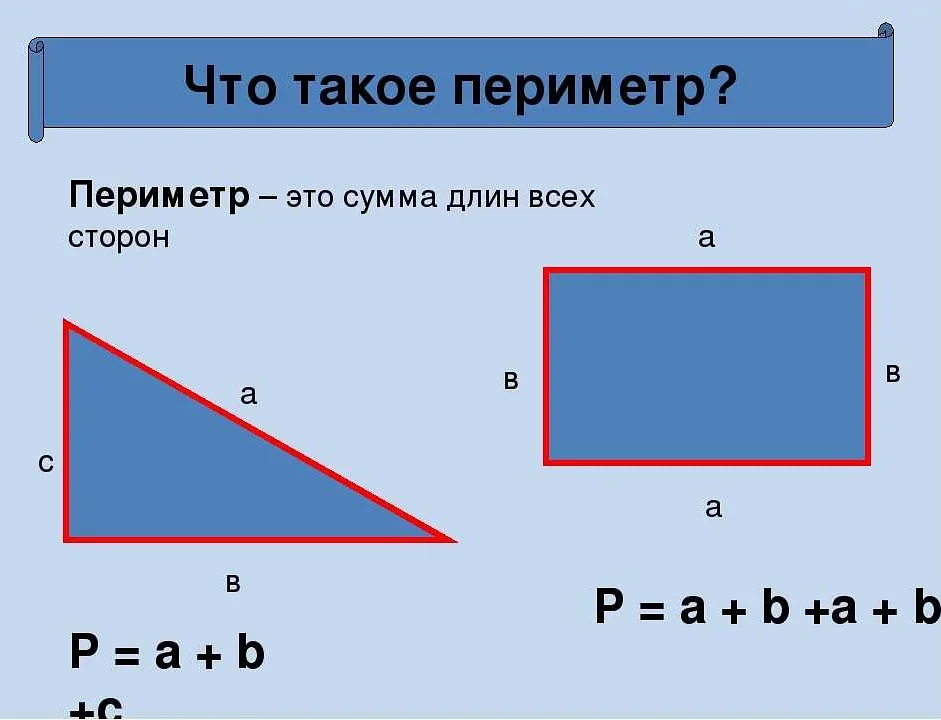
Можно ли вычислить площадь квадрата, зная его периметр?

Да, площадь квадрата можно вычислить, зная его периметр. Для этого нужно знать формулу, связывающую площадь и периметр квадрата. Формула выглядит так: площадь равна половине произведения периметра на длину стороны. Например, если периметр квадрата равен 20 см, то его сторона будет равна 5 см, а площадь — 25 квадратных сантиметров.

Какая единица измерения используется для площади квадрата?

Площадь квадрата измеряется в квадратных единицах. Например, квадратные сантиметры, квадратные метры и т. д.

Как можно найти сторону квадрата, если известна его площадь?

Для нахождения стороны квадрата по известной площади нужно извлечь корень из площади. Например, если площадь квадрата равна 36 квадратным сантиметрам, то его сторона будет равна 6 сантиметрам.

Как посчитать площадь квадрата?

Площадь квадрата рассчитывается по формуле: сторона квадрата в квадрате. Для этого необходимо умножить длину стороны на саму себя.

Какие особенности есть у площади квадрата?

Особенностью площади квадрата является то, что она всегда положительная и не может быть отрицательной. Также, площадь квадрата всегда выражается в квадратных единицах.

Задачи на вычисление площади квадрата

Задачи на вычисление площади квадрата могут быть различными. Вот некоторые из них:

Задача	Описание
Найти площадь квадрата	При данном значении стороны квадрата, необходимо найти его площадь. Формула для вычисления площади квадрата проста: площадь равна квадрату длины стороны.
Найти сторону квадрата	При заданной площади квадрата, необходимо найти длину его стороны. Для этого нужно извлечь квадратный корень из площади.
Найти площадь прямоугольника, зная сторону квадрата	При заданной стороне квадрата, найти площадь прямоугольника, у которого одна сторона равна стороне квадрата, а другая сторона задана.
Найти площадь фигуры, состоящей из нескольких квадратов	При заданном количестве квадратов и их стороне, найти площадь фигуры, состоящей из этих квадратов. Для этого нужно сложить площади всех квадратов.

Это лишь некоторые примеры задач на вычисление площади квадрата. В реальной жизни понимание площади квадрата может быть полезным при решении различных задач, связанных с планировкой, конструированием и измерением площадей.

Практическое применение площади квадрата

Одним из практических применений площади квадрата является расчет площади участка земли. Если участок имеет форму квадрата, то для определения его площади достаточно знать длину одной из его сторон. Площадь квадрата можно легко вычислить по формуле: площадь = сторона * сторона. Например, если сторона квадрата равна 5 метров, то его площадь будет равна 25 квадратным метрам.

Еще одним примером применения площади квадрата является расчет площади поверхности. Например, если известна площадь одной стороны квадрата, можно легко вычислить площадь поверхности куба, образованного этим квадратом. Для этого необходимо умножить площадь одной стороны на 6, так как куб имеет 6 граней. Например, если площадь одной стороны квадрата равна 9 квадратным метрам, то площадь поверхности куба будет равна 54 квадратным метрам.

Также площадь квадрата может использоваться для расчета площади других фигур. Например, площадь прямоугольника можно вычислить, зная площадь квадрата и соотношение сторон прямоугольника к стороне квадрата.