Математическая модель: понятие, виды и примеры применения в реальной жизни

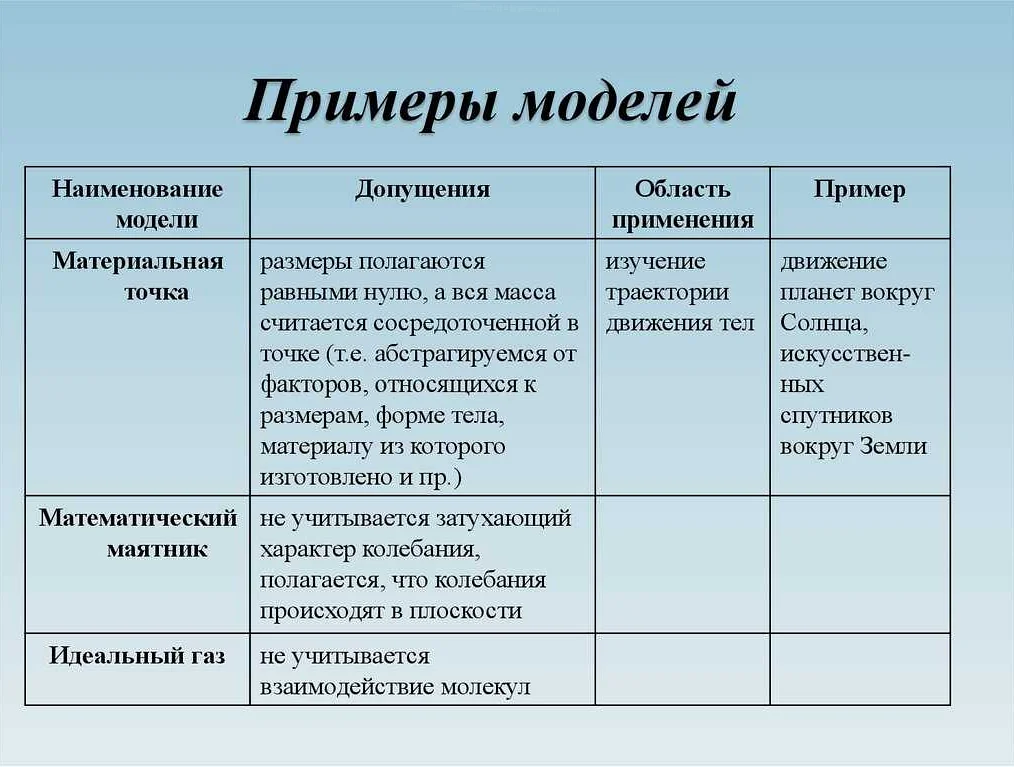
Математическая модель — это способ представления реальных явлений или объектов с помощью формализованных математических схем. Она позволяет упростить изучение и анализ конкретной ситуации и решить проблему в экономических, технических, медицинских и других областях. Статья расскажет, как строятся математические модели и какие виды они существуют.

Математическая модель представляет собой схему или формулу, которая описывает какую-либо систему или процесс. Это может быть абстрактный объект, который включает в себя физические, биологические, экономические и другие аспекты. Моделирование — это один из методов научных исследований, позволяющий анализировать данные и делать прогнозы.

Чтобы создать математическую модель, необходимо определить параметры, которые будут учитываться. Это может быть количество объектов, время, затраты, возможные риски и многое другое. Затем, используя математические методы, эти параметры будут связаны друг с другом.

Как только математическая модель создана, она может быть использована для прогнозирования возможных развитий событий, анализа исходов, выбора оптимальных решений и многое другое. Таким образом, математическая модель является неотъемлемой частью научных исследований и имеет широкое применение в различных сферах науки и технологий.

Определение математической модели

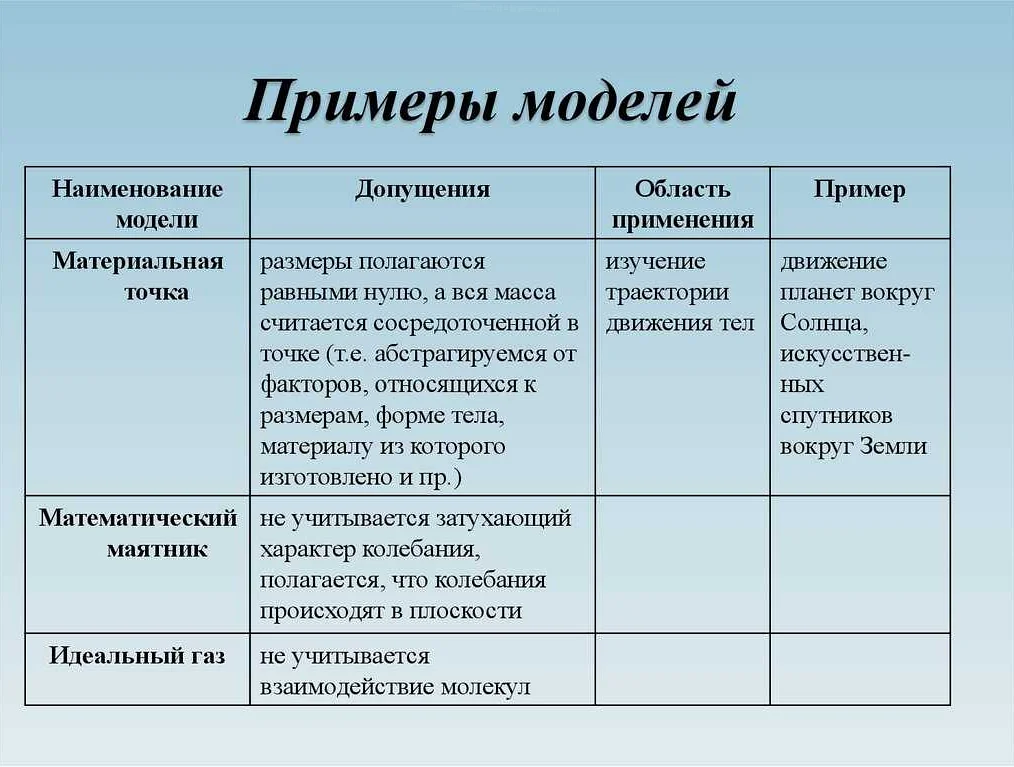
Математическая модель — это абстрактное описание реальной системы или явления, выраженное в математических терминах и символах.

Такая модель может быть использована для различных целей, например, для прогнозирования поведения системы в условиях изменения ее параметров, для оптимизации управления процессами, для проектирования новых технических устройств и многих других приложений.

Одной из особенностей математических моделей является их способность обобщать информацию о системе, содержащей множество факторов и вариантов развития, в относительно простую формулу или уравнение, что позволяет более эффективно изучать и анализировать объекты и явления реального мира.

Однако важно понимать, что математическая модель всегда является лишь приближением к реальной системе, и ее точность и предсказательная способность зависят от корректности выбранных параметров и определяющих ее законов и формул.

Создание математической модели является важным этапом в решении задач, связанных с изучением и управлением сложными системами, и требует глубоких знаний исследуемого объекта и математических методов его описания и анализа.

Видео по теме:

Зачем нужна математическая модель

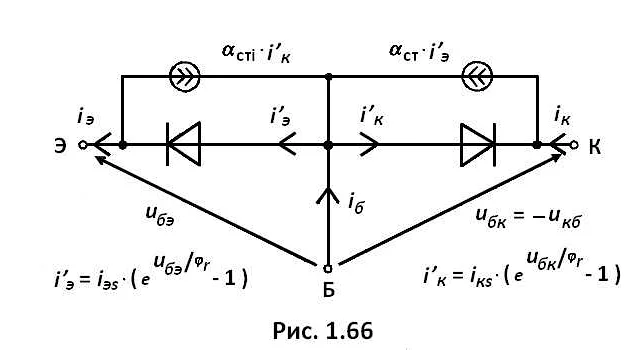
Математическая модель — это упрощенное описание реального объекта или процесса, которое позволяет проводить исследования и прогнозировать результаты без необходимости проведения экспериментов на реальных объектах.

Создание математической модели позволяет оценить эффективность различных решений на основе имитационного моделирования и проведения компьютерных экспериментов. Это особенно важно в областях, где проведение реальных экспериментов невозможно или нецелесообразно, например, в медицине, экологии, финансах, аэрокосмической промышленности и многих других областях.

Математическая модель может также помочь улучшить производительность сложных систем и процессов, выявить узкие места в работе системы, спрогнозировать поведение системы в условиях переменных факторов.

В общем, создание математических моделей является неотъемлемой частью научного и технологического прогресса, позволяя более глубоко понимать реальные системы и процессы, повышать их эффективность и оптимизировать работу в широком спектре областей.

Основные принципы создания математической модели

1. Определение цели моделирования. Необходимо понять, для чего создается математическая модель, какую задачу она должна решить. Определить цель моделирования помогает анализ проблемной ситуации и выделение ключевых вопросов.

2. Выбор переменных и их определение. Математическая модель описывает процесс или явление с помощью переменных, значения которых зависят друг от друга. Переменные могут быть качественными и количественными. Необходимо определить выбранные переменные и их значения.

3. Формулировка уравнений модели. На основе выбранных переменных и их значений формулируются уравнения, описывающие взаимосвязь между ними. Уравнения должны быть логически связаны и отражать основные аспекты процесса или явления.

4. Проверка и анализ модели. Созданную математическую модель необходимо проверить на корректность и адекватность. Для этого используются различные методы, например, аналитический анализ, численное решение, эксперименты. По результатам анализа модель может быть уточнена или изменена.

5. Использование и интерпретация результатов. Полученные результаты при помощи математической модели важно правильно интерпретировать и использовать. Они могут помочь в принятии решений, определении стратегии развития, выявлении проблемных зон и т.д.

Вопрос-ответ:

Что такое математическая модель?

Математическая модель — это абстрактное представление реального объекта, явления или системы, которое включает в себя математические формулы, уравнения и графики, описывающие конкретные характеристики этого объекта или системы. Эта модель может использоваться для предсказания поведения этого объекта в различных условиях и для принятия решений по его управлению.

Зачем создавать математическую модель?

Создание математической модели позволяет упростить и наглядно представить сложные процессы и явления, а также проводить эксперименты и исследования в виртуальной среде, что экономит время и ресурсы. Кроме того, создание математической модели помогает выявить закономерности и зависимости между переменными и предсказать возможные последствия изменения этих переменных.

Как создать математическую модель?

Для создания математической модели нужно сначала определить цель моделирования и выбрать данные, которые будут использоваться для построения модели. Затем нужно выбрать математические методы и модели, которые наилучшим образом соответствуют цели моделирования и выбранным данным. После этого нужно произвести анализ полученных результатов и провести калибровку модели, чтобы проверить ее точность и соответствие реальным данным.

Какие математические модели наиболее часто используются?

Наиболее часто используемые математические модели включают в себя дифференциальные уравнения, вероятностные модели, линейную алгебру, статистические модели, модели оптимизации и теорию игр. Конкретный выбор модели зависит от целей моделирования и типа данных, использованных для построения модели.

Какие программы и инструменты могут использоваться для создания математических моделей?

Существует множество программ и инструментов для создания математических моделей, включая MATLAB, R, Python, Wolfram Mathematica и Octave. Каждый из этих инструментов имеет свои особенности и преимущества, и конкретный выбор зависит от задачи и опыта пользователя.

Как проверить точность математической модели?

Для проверки точности математической модели нужно провести калибровку модели. Это можно сделать путем сравнения результатов, полученных с помощью модели, с реальными данными или результатами других моделей. Также можно провести чувствительностный анализ математической модели, чтобы определить, как сильно изменение начальных данных или параметров повлияет на результаты моделирования.

Могу ли я использовать математическую модель для прогнозирования будущих событий?

Да, математическая модель может использоваться для прогнозирования будущих событий и трендов на основе известных данных и статистических методов. Однако следует понимать, что математическая модель не учитывает неопределенность и случайные факторы, которые могут повлиять на результаты. Поэтому прогнозирование на долгосрочный период может быть неточным.

Особенности математической моделирования в разных областях науки

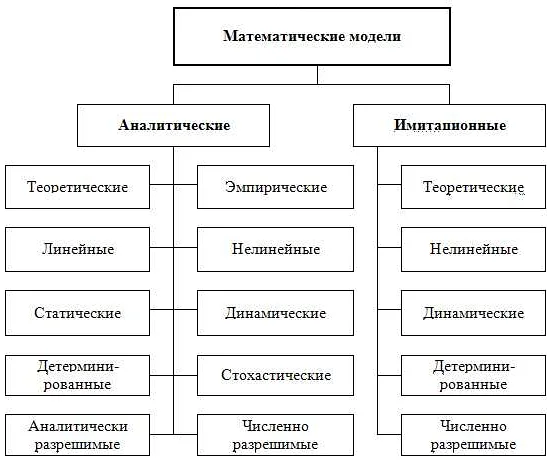
Математическое моделирование – это один из основных способов исследования сложных процессов, которые скрыты от нашего невооруженного глаза. Таким образом, математическое моделирование является незаменимым инструментом в различных областях науки, включая физику, биологию, экономику, социологию и др.

Каждая область науки имеет свои особенности, которые должны быть учтены при создании математической модели. В физике, например, математические модели используются для описания движения объектов, определения свойств веществ и т.д. В то же время, математические модели в биологии помогают выявлять закономерности в функционировании живых организмов и т.д.

В экономике математические модели используются для анализа экономических процессов, прогнозирования экономического развития и т.д. В социологии детальное математическое моделирование может помочь в выявлении тенденций поведения в различных социальных группах и формировании социальных систем.

Из всего вышесказанного можно заключить, что математическое моделирование – это очень важный инструмент в методологии исследования в разных областях науки. Однако, также следует отметить, что каждая область науки имеет свои особенности, которые требуют изменения подхода к моделированию.

Стадии создания математической модели: от формулирования задачи до анализа результатов

Создание математической модели — это постоянный процесс, который проходит через несколько этапов. Начиная от формулирования задачи, заканчивая анализом результатов. Рассмотрим эти этапы подробнее.

Формулирование задачи — первый этап создания математической модели. На этом этапе нужно точно определить, в чем заключается задача, какие данные необходимо использовать и какие результаты нужно получить.

Сбор данных — следующий этап создания модели. Здесь необходимо собрать все данные, которые будут использоваться в модели. Это могут быть данные из источников внутри организации, такие как базы данных или файлы Excel, а также данные из внешних источников, таких как отчеты или статистические данные.

Построение модели — третий этап, который включает разработку математических формул и алгоритмов, которые будут использоваться для обработки данных. На этом этапе модель может быть разработана в виде программного обеспечения, которое может быть запущено на компьютере.

Наглядное отображение модели – на этом этапе реализуется отображение модели в удобной форме, которую легко понять пользователю. Для этого можно использовать диаграммы, графики, таблицы, расчетные листы и другие инструменты.

Анализ результатов — последний этап создания математической модели, на котором производится анализ полученных результатов, делаются выводы и расчеты, позволяющие определить эффективность модели. Если результаты не соответствуют требованиям, модель может быть откорректирована согласно формулировке задачи.

Таким образом, каждый этап создания математической модели является неотъемлемой частью всего процесса и важен для достижения цели.

Математические методы, используемые при создании моделей

Создание математической модели – это процесс, который требует знания различных математических методов. Некоторые из них используются в любой математической модели, а некоторые зависят от конкретной области применения модели.

Вот несколько методов, которые обычно используются при создании математических моделей:

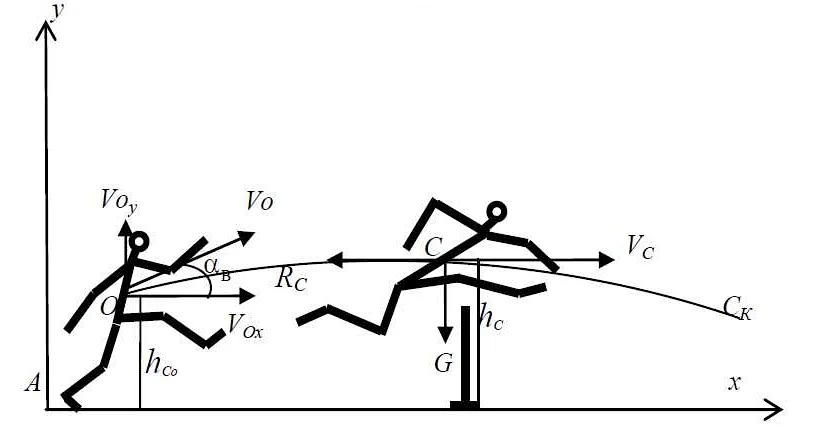
• Аналитическая геометрия – это метод, который используется для изучения геометрических объектов и их свойств, используя математические уравнения. Аналитическая геометрия часто используется при создании моделей, в которых нужно работать с геометрическими объектами, например, при создании моделей движения твердых тел.
• Дифференциальные уравнения – это метод, который используется для описания изменения одной или нескольких переменных с течением времени. Они часто используются при создании моделей, связанных с движением тел или изменениями в состоянии объекта со временем, таких как распространение заболевания.
• Статистика – это метод, который используется для изучения свойств и закономерностей случайных явлений. Статистические методы могут быть полезны при создании математических моделей, например, в экономике или социальных науках.
• Оптимизация – это метод, используемый для нахождения наилучшего решения для определенной задачи при заданных ограничениях. Оптимизация может быть полезна при создании математических моделей, например, при проектировании бизнес-процессов или оптимизации производства.

Примеры практического применения математических моделей

Математические модели широко используются в различных областях науки, техники и бизнеса. Некоторые примеры применения математических моделей включают:

1. Прогнозирование погоды: Метеорологические службы используют математические модели для прогнозирования погоды на основе данных о температуре, барометрическом давлении и других факторах.
2. Финансовая аналитика: Банки, инвестиционные фирмы и другие компании используют математические модели для предсказания цен на акции, оценки рисков и определения оптимальных стратегий инвестирования.
3. Медицинская диагностика: Математические модели используются для анализа медицинских данных и предсказания заболеваний. Например, моделирование распространения болезней позволяет прогнозировать и контролировать их распространение.
4. Транспорт и логистика: Математические модели используются для оптимизации маршрутов, расписаний и других аспектов операций транспортных компаний.
5. Конструирование изделий и материалов: Математические модели используются для определения оптимальных параметров производства и дизайна новых продуктов и материалов.

В целом, математические модели являются универсальным инструментом для анализа и решения разнообразных проблем в науке и бизнесе. Как правило, их создание требует глубоких знаний в области математики, статистики и программирования, но в результате они могут принести значительные выгоды и экономические выгоды.

Преимущества и недостатки математических моделей

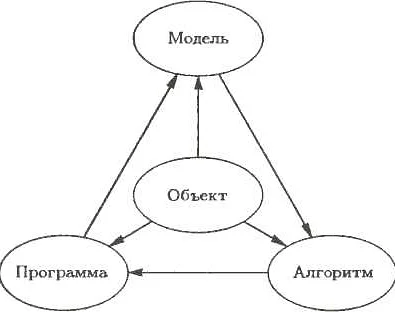
Преимущества:

• Математические модели позволяют анализировать и прогнозировать поведение системы при изменении параметров, что помогает в принятии решений;
• Математические модели позволяют проводить исследования в условиях экономии времени и финансовых ресурсов, которые в противном случае требовали бы больших затрат;
• Математические модели являются инструментом для нахождения оптимальных решений задач, особенно в случаях, когда аналитические методы не позволяют это сделать;
• Математические модели могут служить основой для создания программ и компьютерных систем управления, что позволяет автоматизировать ряд процессов.

Недостатки:

• Математические модели могут быть не совсем точными из-за ограниченности информации и неучтенных факторов;
• Иногда математические модели требуют сложных вычислений и наличия специализированного оборудования для их создания и работы;
• В случае неточности модели или изменения входных данных, ее результаты могут быть неправильными и привести к ошибкам при принятии решений;
• Не все процессы могут быть описаны и моделированы с помощью математических методов, что может приводить к ограничению возможностей моделирования.

Сравнение математических моделей с другими методами исследования

Математическое моделирование – это один из самых сильных инструментов исследования сложных процессов и явлений. С помощью математических моделей можно прогнозировать различные эффекты, которые могут возникнуть в реальной жизни. Однако, существуют и другие методы исследования, которые необходимо рассмотреть.

Например, эксперименты могут дать более точные результаты, особенно если их проводят в контролируемых условиях. Однако, проведение экспериментов может быть дорогим и времязатратным процессом. Кроме того, некоторые процессы невозможно воспроизвести в лаборатории, что делает математическое моделирование единственным способом их изучения.

Другим методом исследования является наблюдение. Наблюдение позволяет получить данные о процессе или явлении непосредственно в реальном мире. Однако, наблюдение может быть непродуктивным или привести к неполным или неточным результатам, если процесс не может быть наблюдаемым в течение достаточно длительного периода времени.

В целом, каждый метод исследования имеет свои преимущества и недостатки, и эффективный выбор метода зависит от характера исследуемого процесса или явления. Однако, математические модели могут быть использованы в большинстве случаев, и они могут быть особенно полезны, когда другие методы недоступны или неэффективны.

Разработка математических моделей в будущем: возможные направления

Искусственный интеллект и машинное обучение. Разработка математических моделей для обучения компьютеров обнаруживает все больший интерес у специалистов. В будущем математические модели машинного обучения будут нужны не только программистам, но и специалистам по медицине, финансам, производству, науке и технике.

Развитие квантовых технологий. Квантовые компьютеры идеально подходят для того, чтобы решать сложные математические проблемы, для которых обычные компьютеры могут потребовать миллионы лет. Разработка математических моделей для квантовых компьютеров будет важным направлением развития науки и технологий в будущем.

Системы управления и оптимизации. Развитие математических моделей, которые позволят выявлять оптимальные решения в тех или иных областях жизни, будет востребовано в будущем. Модели управления и оптимизации могут быть использованы в области транспорта, промышленности, энергетики, финансов и многих других сферах.

Моделирование и исследование мозга. Разработка математических моделей для мозга — одно из перспективных направлений. Эти модели могут помочь понять, как работает наш мозг, что возможно, открыть путь к разработке новых методов лечения различных заболеваний.

Большие данные. В будущем математические модели будут использоваться для анализа больших данных. Это поможет разработать новые методы машинного обучения, выделить новые тенденции в определенных сферах деятельности для улучшения качества жизни людей.

Криптография. Разработка математических моделей для криптографии будет востребована на протяжении всего будущего. Это направление становится все более актуальным, учитывая рост числа кибератак, грабежей и хакерских атак.

• В итоге, разработка математических моделей будет продолжаться в различных направлениях
• в том числе в области машинного обучения, квантовых технологий, систем управления и оптимизации, моделирования мозга, анализа больших данных и криптографии.