Как создать математическую модель объекта представления: полное руководство

Узнайте, как математическая модель объекта представляется, что это такое и как ее использование помогает в разных областях науки и техники. Получите подробную информацию и примеры математических моделей в нашей статье.

Представление объекта в математической форме это необходимый этап при решении многих задач. Оно упрощает анализ объекта и позволяет получать ценные выводы, которые даже не учитывались на первый взгляд. Но как правильно представить объект в математической форме и какие инструменты использовать для решения задач?

В данной статье мы рассмотрим основные понятия и методы представления объектов в математическом виде, а также покажем, как использовать эти знания на практике. Вы узнаете, что такое математическое моделирование и какие задачи оно позволяет решать. Мы рассмотрим различные типы моделей и детально разберем примеры из реальной жизни.

Кроме того, в статье будет дано описание математических понятий, которые необходимы при работе с моделями. Вы узнаете, что такое функция, график, дифференциал и производная. Эти концепции помогут вам понимать математическую модель объекта и использовать ее для решения задач.

Концепция математической моделирования

Математическая модель представляет собой абстрактное описание реального объекта или явления. Концепция математической моделирования заключается в том, что путем использования математических методов можно разработать такую модель, которая будет отражать основные характеристики и закономерности объекта.

С помощью математической модели можно проводить исследования и эксперименты, не задействуя реальный объект. Это сокращает затраты на исследования и позволяет быстрее получать результаты.

Математическая модель может служить инструментом прогнозирования поведения объекта в различных условиях или при изменении параметров. Таким образом, она позволяет принимать решения на основе предсказаний и минимизировать риски.

Важным аспектом при создании математической модели является ее проверка и верификация. Это достигается сравнением результатов, полученных при использовании модели, с реальными данными и экспериментами.

Использование математической модели позволяет оптимизировать процессы и повысить эффективность работы объекта. Она также помогает улучшить понимание объекта и открыть новые закономерности и связи.

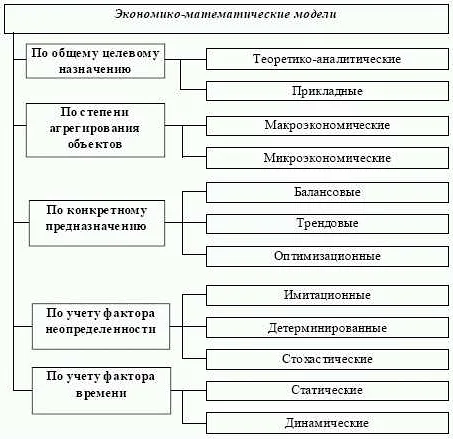
Основные типы математических моделей

1. Эмпирические модели

Эмпирические модели основаны на данных, экспериментальных наблюдениях и статистических методах. Они описывают зависимости между переменными на основе фактических данных. Этот тип моделей используется там, где необходимо проанализировать и предсказать поведение системы на основе имеющихся данных.

2. Аналитические модели

Аналитические модели строятся на основе математических уравнений. Они позволяют найденные решения для системы, описывающей ее поведение во времени. Этот тип моделей используется там, где известны математические свойства системы и её поведение на основе этих свойств.

3. Геометрические модели

Геометрические модели позволяют представить структуру системы и описать ее форму. Они могут использоваться для анализа геометрических параметров системы, способов расположения элементов, формы объекта и т.д. Этот тип моделей используется во многих областях, включая архитектуру, машиностроение, компьютерное моделирование.

4. Случайные модели

Случайные модели используют методы статистики, чтобы описать системы, в которых процессы не могут быть точно предсказаны, так как они подвержены случайным факторам. Этот тип моделей может быть полезен для анализа систем с многомерными параметрами или систем, которые подвержены риску или неопределенности.

5. Физические модели

Физические модели описывают законы физики и используются для анализа физических свойств системы. Этот тип моделей используется в тех областях, где необходимо анализировать и предсказывать поведение системы на основе физических законов, таких как механика, электроника, тепловые и ядерные процессы и т.д.

Процесс построения математической модели

Математическая модель позволяет описать исследуемый объект в виде формул, уравнений и графиков. Она является математическим представлением объекта, которое упрощает его изучение и анализ.

Построение математической модели начинается с определения цели, которую необходимо достичь при ее создании. Далее осуществляется сбор и анализ данных, которые будут использованы для создания модели.

После этого выбирается тип математической модели и, если необходимо, осуществляется подбор параметров. Важную роль в создании модели играет выбор математических операций, которые будут использоваться для ее описания.

Полученная математическая модель тестируется на данных, которые не использовались при ее создании, и проводятся оценки ее точности и эффективности. Если модель не удовлетворяет поставленным целям, необходимо внести изменения в параметры или математические операции.

Важно понимать, что математическая модель является лишь абстракцией объекта и не может описать все его свойства и характеристики. Также при создании модели необходимо учитывать ее ограничения и возможности для применения на практике.

Критерии выбора математических моделей

При выборе математической модели для конкретного объекта нужно учитывать ряд критериев. Важными факторами являются:

• Точность модели – чем меньше ошибок в расчетах, тем точнее модель. Но при этом необходимо не переусердствовать, чтобы модель не стала избыточной и не потребляла больше ресурсов, чем необходимо.
• Простота модели – чем проще модель, тем проще ее использовать и меньше ошибок при ее применении. Однако недостаточно простая модель может не учитывать все факторы, влияющие на объект, и давать неточные результаты.
• Доступность данных – модели должны иметь доступ к нужным данным для расчетов. Если данные недоступны или неточны, то это может сильно повлиять на точность модели.
• Время расчетов – некоторые модели требуют больше времени на расчеты, чем другие. При выборе модели необходимо учитывать время, которое требуется для ее применения.
• Сложность объекта – объекты различной сложности требуют разные модели. Например, для простой механической системы подойдет более простая модель, чем для сложных химических процессов.

Оценивая и учитывая все эти критерии, можно выбрать наиболее подходящую математическую модель для конкретного объекта, учитывая все его особенности и требования.

Примеры применения математического моделирования в реальной жизни

1. Прогноз погоды. Математические модели используются для прогнозирования погоды, что помогает сообществу и экономике адаптироваться к изменению погодных условий. Математические модели используют информацию о метеорологических условиях, таких как температура, давление, скорость ветра и влажность воздуха, для создания точных прогнозов погоды.

2. Авиационный транспорт. Математические модели используются для оптимизации маршрутов авиарейсов, расхода топлива, скорости и т. д. Они также могут предоставлять методы прогнозирования внезапных изменений погоды и технических сбоев, что помогает улучшить безопасность полетов.

3. Медицинские исследования. Математические модели используются для моделирования человеческих органов и тканей, что помогает ученым понимать функционирование органов и создавать новые лекарства и методы лечения. Они также могут использоваться для оптимизации расписания приема лекарств и дозировки.

4. Экономика. Математические модели используются для прогнозирования экономических трендов, создания инвестиционных стратегий и оценки финансовых рисков. Они также могут использоваться для анализа рыночных трендов, выявления потенциальных рисков и разработки стратегий маркетинга для компаний.

5. Спортивные мероприятия. Математические модели используются для прогнозирования и определения вероятности успеха в спортивных соревнованиях. Они также могут использоваться для определения оптимального состава команды, разработки стратегий и определения лучших подходов для подготовки и тренировки спортсменов.

Методы анализа математических моделей

Математическая модель объекта — это формализованное описание, которое описывает какие-то физические или технические процессы в виде связей между элементами модели. После создания модели можно приступать к ее анализу.

Существуют различные методы анализа математических моделей, которые позволяют оценить, насколько корректно отражена реальность в модели и насколько точно ею можно пользоваться для проведения различных исследований.

Метод линеаризации используется для оценки линейной зависимости между элементами модели. В процессе линеаризации модель приводится к виду, когда легко выражаются зависимости между ее элементами.

Метод статистического анализа используется для оценки ошибок и погрешностей модели, а также для анализа вариации параметров модели.

Метод чувствительности позволяет оценить надежность и точность результатов, получаемых на основе модели. Он основывается на анализе того, насколько точно должны быть определены начальные параметры модели для получения точного результата.

Методы оптимизации применяются для нахождения оптимальных параметров модели, чтобы достичь максимальной точности и эффективности работы модели.

Метод численного интегрирования используется для расчета динамических процессов, которые невозможно аналитически выразить. Он предполагает создание специальных программ, которые вычисляют значения параметров модели в определенных точках времени.

Таким образом, выбор методов анализа математической модели должен зависеть от конечной цели исследования, доступной математической базы и уровня подготовки исследователя.

Оценка качества математической модели

Оценка качества математической модели необходима для определения ее соответствия реальному объекту или явлению. Для этого можно использовать различные методы и показатели.

Один из важных показателей качества модели является ее точность. Для оценки точности модели используются среднеквадратическая ошибка, средняя ошибка, коэффициент корреляции и другие статистические показатели.

Кроме того, для оценки качества математической модели необходимо проводить сравнение ее прогнозных значений с результатами эксперимента или наблюдений. Если расхождение между прогнозом модели и реальным результатом большое, то модель нуждается в корректировке.

Важно также учитывать реализуемость модели. Для этого необходимо проверить, насколько легко и быстро модель может быть реализована в виде программы или алгоритма.

В целом, оценка качества математической модели является важным этапом ее разработки и используется для того, чтобы убедиться в ее пригодности для решения конкретной задачи.

Способы верификации и валидации математических моделей

Верификация математической модели является процессом проверки ее корректности и соответствия математическим принципам и законам. Для этого проводятся различные тесты и сравнения с реальными наблюдениями и экспериментальными данными.

Валидация математической модели предполагает проверку ее точности и надежности в предсказании результатов, основываясь на сравнении с реальными наблюдениями и экспериментальными данными. Данный процесс требует установления критериев сравнения и метрик для оценки точности и надежности модели.

Существует несколько методов, которые могут быть использованы для верификации и валидации математической модели:

1. Аналитические методы – основанные на математическом анализе и решении уравнений, формулирующих модель. Они позволяют вычислить точные значения и провести формальную проверку соответствия модели математическим принципам.
2. Экспериментальные методы – основанные на наблюдениях и экспериментах, проведенных с реальным объектом или его аналогом. Эти методы позволяют проверить соответствие модели реальным данным и дать возможность оценить ее точность.
3. Компьютерное моделирование – позволяет создать виртуальную среду, где модель будет работать, и оценить ее точность и надежность в различных условиях. Этот метод может быть основан на численных расчетах, статистических методах или методах машинного обучения.

Процесс верификации и валидации математической модели является очень важным и может занять значительное время и усилия, но он необходим для того, чтобы обеспечить достоверность и точность результатов, получаемых с помощью модели.

Проблемы математического моделирования

Математическое моделирование – это процесс создания математической модели объекта или явления с целью упрощения, исследования и прогнозирования его поведения. Однако, проблемы в математическом моделировании возникают неизбежно. Среди них:

• Недостаток точных данных – при моделировании реальных объектов невозможно учесть все их свойства и характеристики из-за нехватки информации или сложности.
• Сложность моделей – Иногда создание точной математической модели сложно ввиду сложности применения или же длительного времени применения.
• Непредусмотренные факторы – реальность диктует свои условия, поэтому некоторые факторы могут не учитываться или возникают непредвиденные ситуации при использовании моделей.
• Трудность интерпретации результатов – использование математических моделей требует знания математических методов, что может создавать трудности в интерпретации результатов моделирования и принятии решений.

Несмотря на эти проблемы, математическое моделирование считается одним из самых эффективных и экономических методов в науке и технике. Оно позволяет прогнозировать поведение объектов в различных условиях и ускоряет процесс разработки и создания новых технологий.

Видео по теме:

Вопрос-ответ:

Зачем нужна математическая модель объекта?

Математическая модель объекта необходима для проведения анализа свойств и характеристик этого объекта при помощи математического аппарата. Это позволяет проводить различные исследования и оптимизировать процессы, связанные с данной системой.

Какова структура математической модели объекта?

Структура математической модели объекта включает в себя описание всех его элементов, свойств и закономерностей, которые влияют на его функционирование. Также в структуру входят математические выражения, уравнения и формулы, которые описывают поведение объекта и его взаимодействие с окружающей средой.

Как представить математическую модель объекта в виде графа?

Математическую модель объекта можно представить в виде графа, где каждый элемент модели будет представляться узлом графа, а связи между элементами — ребрами. Таким образом, граф будет отображать все зависимости и взаимодействия между элементами модели.

Как выбрать подходящую математическую модель для конкретного объекта?

Выбор подходящей математической модели зависит от цели и задач, которые ставятся перед исследованием данного объекта. Необходимо учитывать особенности объекта, его свойства и взаимодействие с окружающей средой. Также важно оценить точность и достоверность выбранной модели.

Какие методы могут быть использованы для создания математической модели объекта?

Для создания математической модели объекта могут быть использованы различные методы, такие, как методы оптимизации, кластеризации, регрессионный анализ, анализ временных рядов и другие. Каждый метод имеет свои особенности и может быть применен только для конкретных задач и целей.

Как использовать математическую модель объекта для прогнозирования его поведения?

Для прогнозирования поведения объекта необходимо использовать математическую модель, которая описывает закономерности и зависимости между элементами объекта и его окружающей средой. Для прогнозирования будущего поведения, необходимо провести анализ и оценить динамику изменения параметров модели, а также использовать методы прогнозирования на основе статистических данных.

Как проверить достоверность математической модели объекта?

Для проверки достоверности математической модели объекта необходимо провести ее верификацию и валидацию. Верификация — это проверка корректности модели, то есть соответствия ее математическому описанию. Валидация — это проверка соответствия поведения модели реальному поведению объекта. Также необходимо провести анализ погрешностей и оценить точность прогнозных расчетов.

Преимущества и недостатки математического моделирования

Преимущества:

• Математическая модель позволяет облегчить понимание сложных процессов и явлений, которые нельзя наблюдать непосредственно.
• Моделирование помогает прогнозировать поведение объектов в разных условиях, что дает возможность принимать решения о допустимости различных вариантов развития событий.
• С помощью математических моделей можно проводить эксперименты без риска для жизни и здоровья людей или животных и/или существенного ущерба для окружающей среды или социума.
• Моделирование может быть использовано в обучающих целях, чтобы дать доступ к знаниям, которые могут быть известны только специалистам в определенной области.
• Математическое моделирование может помочь в создании новых технологий, улучшении существующих или разработке новых технических устройств и систем.

Недостатки:

• Математические модели могут быть неточными из-за ограничений наших знаний и опыта в определенной области.
• Моделирование может быть дорогостоящим, так как требует выделения большого количества времени на сбор данных, проведение научных исследований и разработку соответствующих компьютерных программ.
• Ошибка разработчика в начальных данных может привести к искажению результата, а неверная интерпретация моделирования может стать причиной неправильного принятия решений.
• Моделирование не всегда может учитывать все факторы, влияющие на поведение объекта, что может снизить точность прогноза.
• Высокая сложность моделей может сделать их непригодными для использования в практических целях, так как они потребуют значительных ресурсов для вычисления и применения.

Будущее математического моделирования

Математическое моделирование является неотъемлемой частью современной науки и техники. Без математических моделей сложно представить себе развитие науки таких областей, как физика, механика, биология, экономика и т.д. Однако с развитием технологий возникают новые вызовы для математического моделирования.

Увеличение объема данных и расширение инструментов и технологий обработки данных позволяют собирать все более точную информацию о реальных системах. В связи с этим, широко распространенными становятся нейронные сети и алгоритмы машинного обучения, которые позволяют выделить закономерности в данных. В будущем, математическое моделирование будет еще более тесно связано с анализом больших объемов данных и будут создаваться более сложные модели для обработки данных.

Также, в будущем математическое моделирование будет тесно связано с развитием квантовых вычислений. Это позволит создавать более точные и эффективные модели для анализа сложных систем и прогнозирования их поведения. Квантовое моделирование уже используется в таких областях, как молекулярное моделирование и симуляции сложных химических реакций.

Таким образом, будущее математического моделирования будет тесно связано с развитием технологий обработки данных и квантовых вычислений. Это позволит создавать более точные и эффективные модели для анализа и прогнозирования поведения сложных систем.