Математические модели в которых случайные факторы учитываются

Математические модели, в которых учитываются случайные факторы, представляют собой эффективный инструмент для анализа и прогнозирования различных явлений. Узнайте, какие методы и подходы используются для моделирования случайных процессов и как это помогает улучшить точность прогнозов и принимать более обоснованные решения.

Математическое моделирование является важным инструментом для изучения и понимания сложных явлений в различных областях науки и техники. Однако, часто в реальном мире существуют случайные факторы, которые могут влиять на результаты моделирования. Для учета этих случайных факторов используются математические модели с учетом случайности.

Математические модели с учетом случайных факторов основаны на теории вероятностей и статистике. Они позволяют учесть случайные воздействия на систему и предсказать вероятные результаты в различных сценариях. Такие модели широко применяются в физике, экономике, финансах, биологии, и других научных и технических областях.

Применение математических моделей с учетом случайных факторов имеет большое значение в прогнозировании и принятии решений. Они позволяют оценить вероятности различных событий и их влияние на систему. Например, в экономике такие модели используются для прогнозирования курсов валют, цен на акции, рисков финансовых инструментов и т.д. В биологии они помогают изучать эволюцию популяций, распространение инфекционных заболеваний и другие биологические процессы.

Использование математических моделей с учетом случайных факторов требует не только знаний в области математики и статистики, но и умения анализировать и интерпретировать полученные результаты. Кроме того, такие модели требуют большого объема данных для точных и достоверных прогнозов. Однако, они позволяют получить более реалистичные и полные представления о системе, что делает их незаменимыми инструментами для прогнозирования и принятия решений в современном мире.

Роль математических моделей в анализе случайных факторов

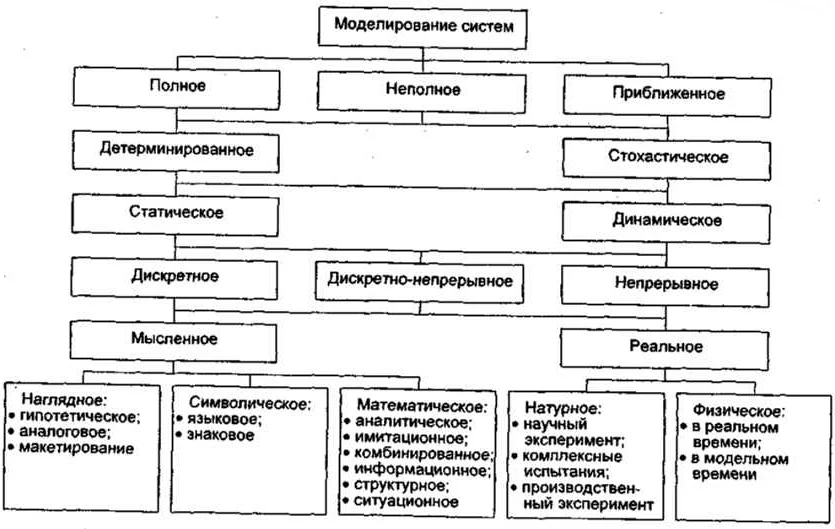
Случайные факторы играют важную роль во многих областях жизни, от финансовых рынков до биологических процессов. Они могут вносить неопределенность и усложнять анализ и прогнозирование. Для того чтобы лучше понять и управлять случайными факторами, используются математические модели.

Математические модели позволяют описывать и предсказывать поведение случайных факторов с помощью формул, уравнений и статистических методов. Они позволяют анализировать вероятности различных событий, оценивать риски, строить прогнозы и принимать решения на основе данных.

Математические модели с учетом случайных факторов основаны на теории вероятностей и статистике. Они позволяют строить вероятностные распределения, моделировать случайные величины и исследовать их взаимосвязи. Это помогает улучшить понимание случайных факторов и сделать более точные прогнозы.

Применение математических моделей с учетом случайных факторов распространено во многих областях, таких как финансы, экономика, климатология, медицина и технические науки. Например, в финансовой сфере моделирование случайных факторов помогает оценивать риски инвестиций и прогнозировать доходность портфеля. В медицине моделирование случайных факторов может помочь предсказать эффективность лекарственных препаратов и оценить вероятность возникновения побочных эффектов.

Использование математических моделей с учетом случайных факторов позволяет сделать анализ и прогнозирование более точными и надежными. Они помогают улучшить понимание случайных факторов и принимать рациональные решения на основе вероятностных оценок. Таким образом, математические модели играют важную роль в анализе случайных факторов и помогают управлять рисками и неопределенностью в различных областях жизни.

Статистические методы моделирования случайных процессов

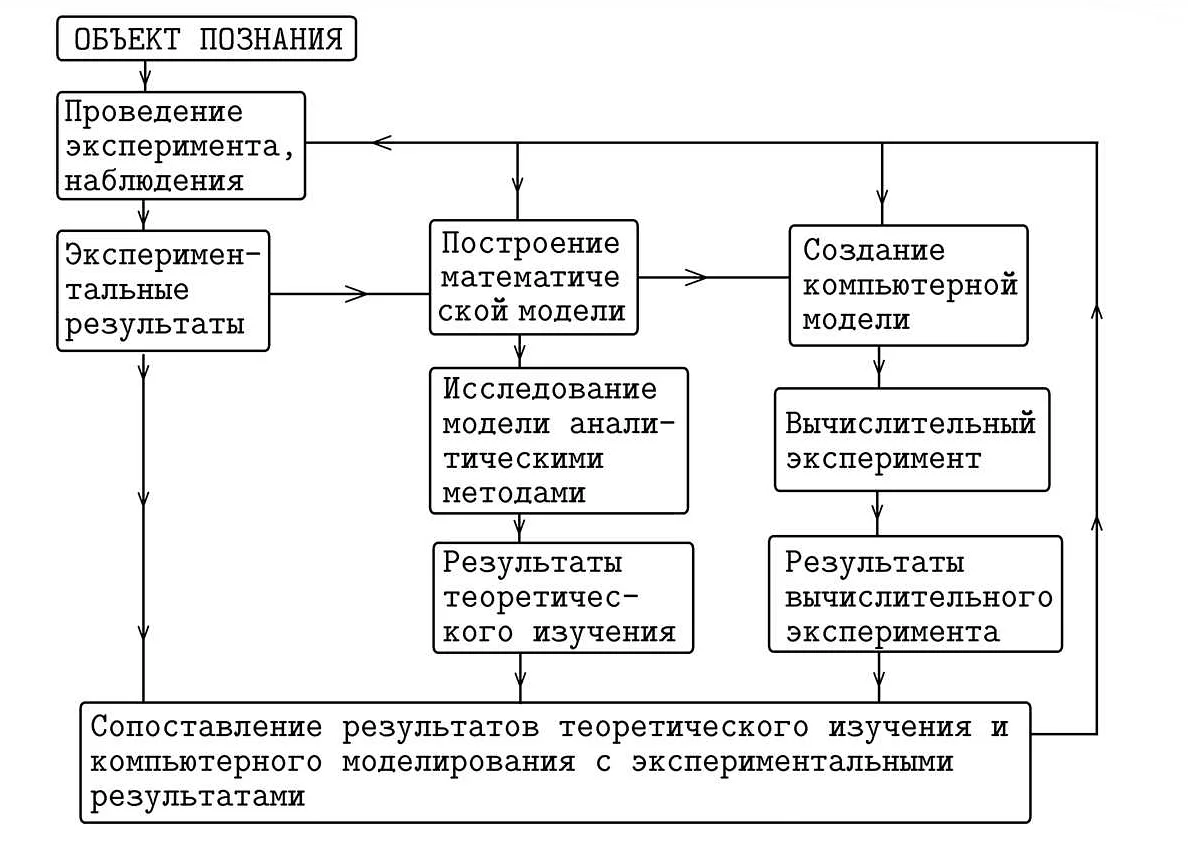
Одним из основных инструментов статистического моделирования является построение вероятностных моделей. Вероятностная модель представляет собой математическую модель, которая описывает случайный процесс в терминах вероятностных закономерностей.

Для построения вероятностной модели необходимо иметь статистические данные о случайном процессе. Эти данные могут быть получены путем наблюдения случайного процесса или путем проведения экспериментов. На основе этих данных можно построить эмпирическое распределение, которое описывает вероятностные закономерности случайного процесса.

Одним из основных подходов в статистическом моделировании является метод максимального правдоподобия. Суть метода заключается в поиске таких параметров модели, при которых вероятность наблюдаемых данных будет максимальной. Это позволяет найти наиболее вероятные значения параметров модели и смоделировать случайный процесс с их помощью.

Кроме метода максимального правдоподобия, существует также ряд других статистических методов моделирования случайных процессов, таких как метод моментов, метод наименьших квадратов и методы байесовской статистики. Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной задачи моделирования.

МетодОписание

Метод максимального правдоподобия	Нахождение параметров модели, при которых вероятность наблюдаемых данных будет максимальной
Метод моментов	Нахождение параметров модели, при которых статистические моменты наблюдаемых данных будут равны соответствующим моментам модели
Метод наименьших квадратов	Нахождение параметров модели, при которых сумма квадратов отклонений наблюдаемых данных от значений модели будет минимальной
Методы байесовской статистики	Использование априорной информации о параметрах модели для получения апостериорных распределений этих параметров

Статистические методы моделирования случайных процессов широко применяются в различных областях, таких как финансы, экономика, метеорология, биология и многие другие. Они позволяют анализировать и предсказывать различные случайные явления и принимать обоснованные решения на основе статистических данных.

Важность учета случайных факторов в прогнозировании

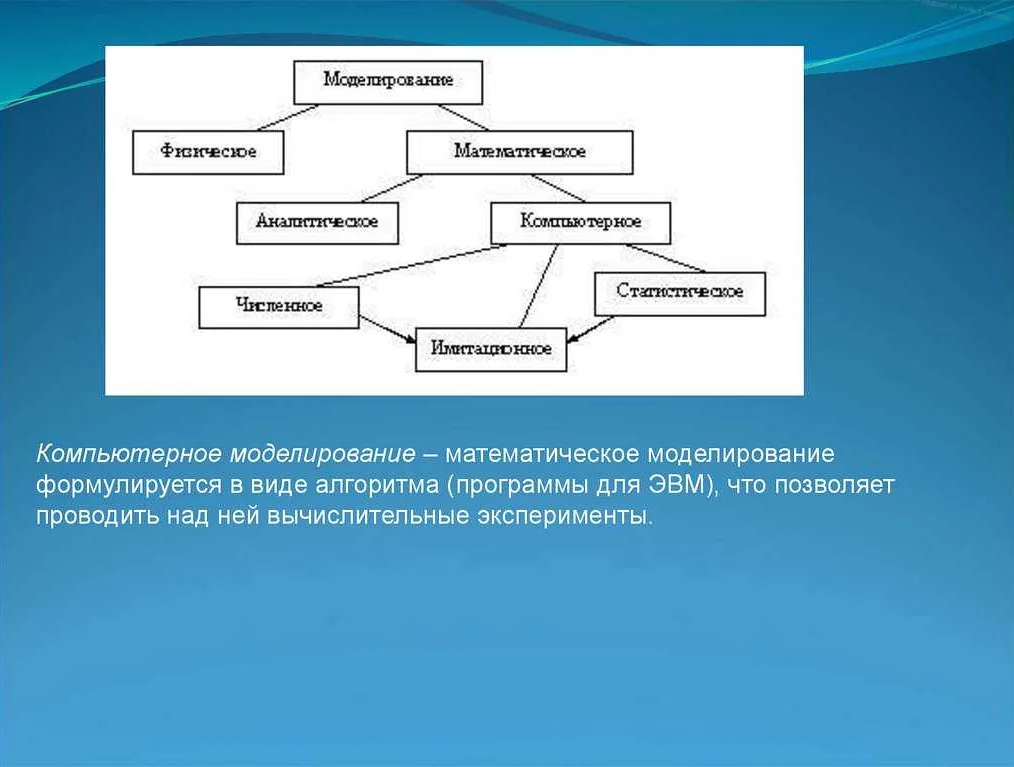
Случайные факторы могут включать в себя такие переменные, как случайные изменения в спросе и предложении, случайные колебания на финансовых рынках, случайные изменения в погодных условиях и т.д. Эти факторы могут быть непредсказуемыми и изменяться во времени, что затрудняет точное прогнозирование.

Учет случайных факторов в математических моделях позволяет улучшить точность прогнозирования. Случайные факторы могут быть моделированы с помощью вероятностных распределений, таких как нормальное распределение или распределение Пуассона. Эти распределения позволяют оценить вероятность различных значений случайных факторов и учесть их в прогнозе.

Кроме того, учет случайных факторов позволяет оценить риски и неопределенности прогноза. Вероятностные модели позволяют проводить анализ чувствительности и оценивать вероятность возникновения различных сценариев. Это помогает принимать более обоснованные решения на основе прогнозов.

В целом, учет случайных факторов является неотъемлемой частью прогнозирования и позволяет улучшить точность и надежность прогнозов. Он позволяет учитывать непредсказуемость и изменчивость реального мира, что особенно важно в условиях неопределенности.

Применение математических моделей в финансовой сфере

Одной из самых распространенных математических моделей, используемых в финансовой сфере, является модель Блэка-Шоулза. Она используется для оценки цен на опционы, которые являются финансовыми инструментами, дающими право на покупку или продажу активов (например, акций) по заранее оговоренной цене в определенный момент времени. Модель Блэка-Шоулза учитывает различные факторы, включая текущую цену актива, ставку процента, волатильность рынка и время до истечения опциона.

Еще одним примером применения математических моделей в финансовой сфере является модель Варда-Максимова, используемая для оценки кредитного риска. Она позволяет оценить вероятность дефолта заемщика и определить размер кредитного портфеля, который позволит минимизировать риск. Модель Варда-Максимова учитывает различные факторы, такие как кредитный рейтинг заемщика, долговую нагрузку, прибыльность бизнеса и макроэкономические показатели.

Примеры математических моделей в финансовой сфере:Области применения:

Модель Блэка-Шоулза	Оценка цен на опционы
Модель Варда-Максимова	Оценка кредитного риска

Это лишь некоторые примеры применения математических моделей в финансовой сфере. С каждым годом все больше и больше компаний и организаций используют математическое моделирование для принятия решений и улучшения своих финансовых показателей. При этом важно иметь понимание ограничений моделей и учитывать возможные риски, связанные с прогнозированием и принятием решений на основе математических моделей.

Моделирование случайных процессов в экономике

Математическое моделирование играет важную роль в экономике, поскольку позволяет анализировать и прогнозировать случайные процессы, которые влияют на экономическую деятельность. Случайные процессы в экономике могут быть связаны с изменением цен на товары и услуги, колебаниями валютных курсов, флуктуациями рыночных индексов и другими факторами.

Одним из основных инструментов для моделирования случайных процессов в экономике являются стохастические дифференциальные уравнения. Эти уравнения описывают изменение экономических показателей во времени с учетом случайных факторов. Например, модель Блэка-Шоулза используется для оценки цен на финансовые опционы, учитывая случайное движение цены базового актива.

Еще одним методом моделирования случайных процессов в экономике является использование статистических моделей. Например, модель ARIMA (авторегрессионная интегрированная скользящая средняя) может быть применена для анализа и прогнозирования временных рядов с учетом случайных шумов. Эта модель позволяет учитывать тренды и сезонность в данных и предсказывать их будущие значения.

Кроме того, с помощью случайных процессов можно моделировать риски в экономической деятельности. Например, модель Value at Risk (VaR) используется для оценки потенциальных убытков в портфелях инвестиций с учетом случайных колебаний цен на активы. Это позволяет инвесторам принимать взвешенные решения о распределении своих инвестиций и управлении рисками.

В заключение, моделирование случайных процессов в экономике является мощным инструментом для анализа и прогнозирования экономических явлений. Оно позволяет учитывать случайные факторы, которые могут влиять на экономическую деятельность, и принимать взвешенные решения на основе математической модели. Это помогает бизнесам и инвесторам справляться с неопределенностью и рисками, связанными с экономической деятельностью.

Прогнозирование погоды с помощью математических моделей

Математические модели погоды основываются на фундаментальных уравнениях физики атмосферы и океана. Они учитывают такие факторы, как температура, давление, влажность, скорость и направление ветра, а также солнечная радиация. Однако, прогнозирование погоды связано с большим количеством неопределенности и случайных факторов, которые не всегда можно точно учесть.

Для учета случайных факторов в математических моделях используются стохастические методы. Они позволяют учесть случайные колебания в атмосферных условиях и предсказывать вероятность различных погодных событий. Стохастические модели погоды основаны на статистическом анализе и предполагают наличие вероятностных закономерностей в погодных процессах.

Прогнозирование погоды с помощью математических моделей включает несколько этапов. Сначала собираются данные о текущих погодных условиях, включая данные с метеорологических станций, спутников и радаров. Затем эти данные вводятся в математическую модель, которая осуществляет расчеты на основе физических уравнений и статистических методов.

Полученные результаты представляются в виде числовых значений, графиков или карт, которые облегчают интерпретацию и позволяют делать прогнозы на различных временных и пространственных шкалах. Однако, следует отметить, что прогнозы погоды всегда сопряжены с определенной степенью неопределенности и могут быть непрогнозируемыми в случае экстремальных погодных событий.

В целом, прогнозирование погоды с помощью математических моделей является сложной задачей, требующей учета множества факторов и использования стохастических методов. Однако, развитие математических моделей позволяет повысить точность прогнозов и обеспечить более надежные данные для принятия решений в различных сферах деятельности.

Математические модели в медицине: учет случайных воздействий

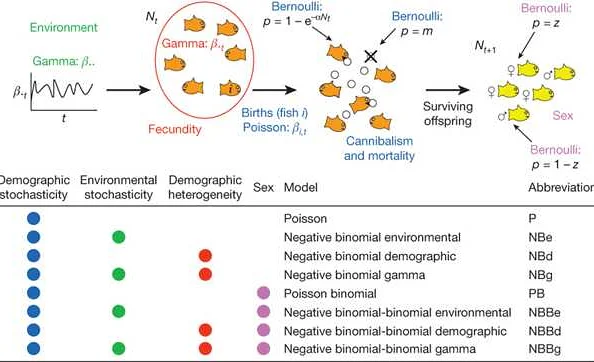
Для того чтобы более точно предсказывать и анализировать такие сложные системы, используются математические модели. Одной из ключевых особенностей таких моделей является учет случайных воздействий.

Случайные факторы в медицине могут быть связаны с различными аспектами, такими как генетическая предрасположенность, окружающая среда, психологические факторы и прочие. Они могут оказывать как положительное, так и отрицательное влияние на состояние пациента или эффективность лечения.

Для учета случайных воздействий в математических моделях в медицине используются различные статистические методы и вероятностные расчеты. Например, метод Монте-Карло позволяет моделировать случайные события и прогнозировать их вероятность в рамках системы.

Математические модели с учетом случайных факторов помогают врачам и исследователям принимать более информированные решения в области диагностики, прогнозирования и планирования лечения. Они позволяют учесть множество факторов, которые могут повлиять на результаты, и предсказать их вероятность или влияние на пациента.

Такие модели могут быть полезными инструментами для разработки индивидуализированного подхода к лечению, а также для оптимизации исследований и экспериментов в медицине.

Вопрос-ответ:

Зачем использовать математические модели с учетом случайных факторов?

Математические модели с учетом случайных факторов позволяют учесть неопределенности и случайности в реальных процессах и явлениях. Они помогают прогнозировать вероятности различных исходов и принимать решения на основе статистических данных.

Какие принципы лежат в основе математических моделей с учетом случайных факторов?

Основными принципами математических моделей с учетом случайных факторов являются вероятностный подход и статистические методы. Вероятностный подход позволяет моделировать случайные величины и оценивать их распределение вероятностей. Статистические методы позволяют анализировать статистические данные и делать выводы о вероятностях различных событий.

Какие области науки применяют математические модели с учетом случайных факторов?

Математические модели с учетом случайных факторов применяются во многих областях науки, включая физику, экономику, финансы, биологию, медицину, психологию и социологию. Они помогают исследователям и практикам прогнозировать вероятности различных событий, оценивать риски и принимать решения на основе статистических данных.

Как можно использовать математические модели с учетом случайных факторов в бизнесе?

В бизнесе математические модели с учетом случайных факторов могут быть использованы для прогнозирования спроса на товары и услуги, оценки рисков инвестиций, оптимизации процессов производства и логистики, анализа данных о клиентах и многих других целей. Они помогают предсказывать вероятности различных исходов и принимать решения на основе статистических данных, что может повысить эффективность и прибыльность бизнеса.

Моделирование рисков в инженерии и строительстве

Моделирование рисков играет важную роль в инженерии и строительстве, поскольку позволяет предсказать и оценить возможные негативные последствия различных событий и принять соответствующие меры для их снижения или предотвращения. Риски в инженерии и строительстве могут быть связаны с различными факторами, такими как нестабильность грунта, неблагоприятные погодные условия, ошибки проектирования или строительства, финансовые проблемы и другие.

Для моделирования рисков в инженерии и строительстве используются различные методы и математические модели. Одним из наиболее распространенных методов является метод Монте-Карло, который позволяет моделировать случайные события и оценивать вероятность их возникновения. Этот метод основан на генерации большого количества случайных чисел и проведении итераций для анализа различных сценариев.

Другим важным инструментом для моделирования рисков в инженерии и строительстве является анализ чувствительности. Этот метод позволяет определить, какие параметры или переменные влияют на результаты моделирования наибольшим образом. Таким образом, можно сосредоточиться на наиболее важных факторах и разработать стратегии для их управления и контроля.

Моделирование рисков также может быть использовано для определения оптимальных решений в инженерных и строительных проектах. Например, можно провести моделирование различных вариантов проекта с учетом возможных рисков и выбрать наилучшее решение, которое минимизирует потенциальные негативные последствия и максимизирует ожидаемую пользу.

В заключение, моделирование рисков является важным инструментом в инженерии и строительстве, который позволяет предсказывать и оценивать возможные негативные последствия и разрабатывать стратегии для их управления. Это помогает повысить эффективность и безопасность инженерных и строительных проектов и минимизировать потери.

Видео по теме: