Что является целью моделирования математики как науки
Содержимое
- 1 Что является целью моделирования математики как науки
- 1.1 Моделирование математики: цель и задачи
- 1.2 Видео по теме:
- 1.3 Поиск истины в математике
- 1.4 Прогнозирование с помощью математических моделей
- 1.5 Вопрос-ответ:
- 1.5.0.1 Зачем математикам нужно моделирование?
- 1.5.0.2 Какие примеры применения моделирования в математике?
- 1.5.0.3 Какие инструменты используются для математического моделирования?
- 1.5.0.4 Как математическое моделирование помогает прогнозировать будущие события?
- 1.5.0.5 Зачем нужно моделирование в математике?
- 1.5.0.6 Какие методы используются в математическом моделировании?
- 1.5.0.7 Как моделирование помогает в поиске истины в математике?
- 1.6 Оптимизация процессов с помощью математического моделирования
- 1.7 Математическое моделирование в научных исследованиях
- 1.8 Применение математических моделей в физике и химии
- 1.9 Математическое моделирование в экономике и финансах
- 1.10 Математическое моделирование в медицине и биологии
Целью моделирования математики как науки является разработка абстрактных и формальных моделей, которые могут быть использованы для анализа и понимания реальных явлений и процессов. Математические модели помогают улучшить наше понимание мира, предсказывать его поведение и принимать обоснованные решения в различных областях знания и применения, включая физику, экономику, биологию и технику.
Математика — это наука, которая изучает структуру, свойства и взаимоотношения чисел, фигур, пространств и других абстрактных объектов. Одним из главных аспектов математики является моделирование, которое позволяет создавать формальные представления реальности и анализировать их с помощью математических методов.
Цель моделирования в математике состоит в поиске истины. Математика стремится открыть фундаментальные принципы, которые описывают нашу вселенную и устанавливают правила, с которыми она функционирует. Моделирование позволяет математикам формулировать гипотезы и выводить логические следствия, которые могут быть проверены экспериментально или доказаны аналитически.
Однако моделирование математики не ограничивается только поиском истины. Оно также используется для прогнозирования будущих событий и оптимизации процессов. Математические модели могут помочь предсказать развитие сложных систем, таких как погода, финансовые рынки или популяция живых организмов. Они также могут быть использованы для оптимизации различных процессов, например, в производстве или логистике, чтобы достичь наилучших результатов при заданных ограничениях.
Моделирование математики является мощным инструментом, позволяющим исследовать и понимать сложные явления и процессы. Оно помогает нам не только понять мир вокруг нас, но и принимать обоснованные решения, которые могут положительно влиять на нашу жизнь и окружающую среду.
В итоге, моделирование в математике играет важную роль в науке, позволяя нам углубиться в понимание фундаментальных законов природы, предсказывать будущие события и оптимизировать различные процессы. Оно помогает нам расширить границы нашего познания и применить наше знание для достижения значимых результатов.
Моделирование математики: цель и задачи

Целью моделирования математики является поиск истины. Математические модели разрабатываются для того, чтобы понять и объяснить законы и принципы, лежащие в основе реальности. Моделирование позволяет исследовать сложные системы, предсказывать их поведение и прогнозировать будущие события.
Основной задачей моделирования математики является оптимизация. Математические модели позволяют найти наилучшие решения, оптимальные стратегии и оптимальные условия для различных задач. Они позволяют улучшить процессы и результаты в различных областях, включая экономику, науку, технику, физику и многие другие.
Моделирование математики имеет широкий спектр применений. Оно используется в различных областях науки и техники для решения сложных задач и улучшения процессов. Благодаря моделированию математики мы можем получить новые знания, предсказывать будущие события и улучшать наши жизни во многих аспектах.
Видео по теме:
Поиск истины в математике
Математика изначально задумана как наука, направленная на поиск истины. Цель математиков заключается в открытии и доказательстве математических фактов, которые считаются истинными независимо от человеческого мнения. Математические теоремы основываются на логическом рассуждении и строгих доказательствах, что позволяет прийти к истинным выводам.
Поиск истины в математике основан на аксиоматическом подходе. Математические системы строятся на основе некоторого набора аксиом, которые принимаются без доказательства. Затем, с помощью логических законов и рассуждений, выводятся новые утверждения, которые могут быть доказаны или опровергнуты.
Доказательства играют ключевую роль в поиске истины в математике. Доказательство математической теоремы — это логическая цепочка рассуждений, которая позволяет убедиться в истинности данного утверждения. Доказательства могут быть построены различными способами, включая индукцию, от противного, конструктивные и не конструктивные доказательства.
Математическая истина является абсолютной и неизменной. Если математическое утверждение доказано, то оно считается истинным в рамках данной математической системы. Однако, существуют математические проблемы, которые до сих пор остаются нерешенными, и вопрос о их истинности остается открытым.
Поиск истины в математике также связан с понятием неразрешимости. Некоторые математические проблемы невозможно решить с помощью существующих математических методов. Это открытые вопросы, требующие новых идей и подходов для их решения.
В итоге, поиск истины в математике является основной целью математической науки. Открытие новых математических фактов и доказательство их истинности позволяют расширять наше понимание мира и применять математику в различных областях, включая физику, экономику, информатику и другие.
Прогнозирование с помощью математических моделей
Прогнозирование с помощью математических моделей основано на анализе и обработке статистических данных. В основе прогнозов лежат закономерности, выявленные в исторических данных. С помощью математических методов, таких как регрессионный анализ, временные ряды, искусственные нейронные сети и другие, строятся модели, которые позволяют предсказывать будущие значения переменных.
Прогнозирование имеет большое значение в науке и практике. С помощью прогнозов можно определить будущую тенденцию развития явления, принять обоснованные решения и планировать дальнейшие действия. Например, в экономике прогнозы позволяют прогнозировать рост или спад рынка, в финансах – предсказывать курс валют и цены на акции.
Однако прогнозы не всегда являются абсолютно точными. Они основаны на имеющихся данных и предположениях о закономерностях. В реальности могут возникать непредвиденные обстоятельства, которые могут изменить предсказанные результаты. Поэтому важно использовать прогнозы как инструмент, а не единственный источник информации при принятии решений.
Прогнозирование с помощью математических моделей является существенной частью научного исследования и практической деятельности. Оно позволяет предсказывать будущие события и явления, оптимизировать процессы и принимать обоснованные решения. С каждым годом развитие математических моделей и методов прогнозирования становится все более точным и эффективным, что позволяет улучшить качество прогнозов и повысить эффективность принимаемых решений.
Преимущества прогнозирования с помощью математических моделей:Недостатки прогнозирования с помощью математических моделей:
| — Возможность предсказывать будущие значения переменных | — Прогнозы могут быть неточными из-за непредвиденных обстоятельств |
| — Объективность и научная обоснованность | — Необходимость наличия достаточного объема исходных данных |
| — Возможность оптимизации процессов и принятия обоснованных решений | — Возможность ошибок в выборе математической модели |
Вопрос-ответ:
Зачем математикам нужно моделирование?
Математики используют моделирование для решения различных задач. Во-первых, моделирование помогает им исследовать и понять сложные системы, которые могут быть слишком сложными для анализа аналитическими методами. Во-вторых, моделирование позволяет математикам прогнозировать поведение системы в будущем и оптимизировать ее работу. Наконец, моделирование является инструментом для поиска математической истины и проверки гипотез.
Какие примеры применения моделирования в математике?
Примеры применения моделирования в математике многочисленны. Например, моделирование используется для изучения физических процессов, таких как движение тела или распространение звука. Оно также применяется в экономике для анализа рыночных трендов и прогнозирования экономического развития. Еще одним примером является использование моделирования в биологии для изучения эволюции и распространения заболеваний.
Какие инструменты используются для математического моделирования?
Для математического моделирования используются различные инструменты. Одним из основных инструментов является символьное и численное программное обеспечение, такое как MATLAB, Mathematica и Python. Эти программы позволяют математикам создавать и решать математические модели. Кроме того, используются такие методы, как дифференциальные уравнения, статистика и оптимизация, которые помогают анализировать и решать моделировочные задачи.
Как математическое моделирование помогает прогнозировать будущие события?
Математическое моделирование позволяет математикам анализировать данные и строить модели, которые описывают поведение системы. Затем эти модели могут быть использованы для прогнозирования поведения системы в будущем. Например, моделирование может использоваться для прогнозирования погоды, финансовых рынков или распространения эпидемий. Важно отметить, что прогнозы могут быть приближенными и зависеть от точности модели и входных данных.
Зачем нужно моделирование в математике?
Моделирование в математике выполняет несколько целей. Во-первых, оно позволяет исследовать и понять сложные системы и явления, которые нельзя изучить напрямую. Модели помогают нам визуализировать и анализировать эти системы, выявлять их закономерности и свойства. Во-вторых, моделирование позволяет прогнозировать будущие события и результаты на основе имеющихся данных и известных законов. Это особенно полезно в науках, где важно предсказать поведение системы или сделать выводы о ее будущих состояниях. И, наконец, моделирование позволяет оптимизировать процессы и принимать научно обоснованные решения. Математические модели помогают нам найти оптимальные решения, минимизирующие затраты или максимизирующие выгоды.
Какие методы используются в математическом моделировании?
В математическом моделировании используются различные методы в зависимости от системы или явления, которые мы изучаем. Одним из основных методов является дифференциальное моделирование, когда система описывается с помощью дифференциальных уравнений. Этот метод широко используется для моделирования динамических процессов. Другим популярным методом является статистическое моделирование, когда мы используем статистические методы для анализа данных и построения модели на основе этих данных. Существуют также методы математического программирования, оптимизации и теории игр, которые используются для решения оптимизационных задач. Все эти методы имеют свои преимущества и ограничения, и выбор метода зависит от конкретной задачи.
Как моделирование помогает в поиске истины в математике?
Моделирование в математике позволяет нам исследовать различные гипотезы и проверять их на истинность. Мы можем создавать математические модели, которые описывают различные явления или системы, и затем проверять их с помощью математического анализа и экспериментов. Если модель соответствует наблюдаемым данным и прогнозирует будущие события, то мы можем считать ее истинной или, по крайней мере, приближенной к истине. Однако важно помнить, что математическая истина не всегда совпадает с реальной истиной, поэтому моделирование всегда является лишь приближением.
Оптимизация процессов с помощью математического моделирования
Одной из основных целей оптимизации процессов является достижение максимальной эффективности при ограниченных ресурсах. Математическое моделирование позволяет учесть все факторы, влияющие на процесс, и найти такие параметры, при которых достигается наилучший результат.
Математическое моделирование процессов может быть представлено в виде функциональной зависимости между входными и выходными параметрами. С помощью этой модели можно оптимизировать различные параметры процесса, такие как время выполнения, стоимость ресурсов, качество продукции и другие.
Для проведения оптимизации процессов необходимо разработать математическую модель, которая адекватно описывает процесс и учитывает все его особенности и ограничения. Затем проводится анализ модели, находятся оптимальные значения параметров и определяются наилучшие стратегии действий.
Применение математического моделирования для оптимизации процессов позволяет сократить время и затраты на испытания и эксперименты на практике. Более того, такой подход позволяет получить результаты, которые могут быть трудно или невозможно получить с помощью других методов.
Таким образом, математическое моделирование является мощным инструментом для оптимизации процессов в различных областях. Он позволяет находить наилучшие решения, учитывая все факторы и ограничения, и достигать максимальной эффективности процессов при ограниченных ресурсах.
Математическое моделирование в научных исследованиях
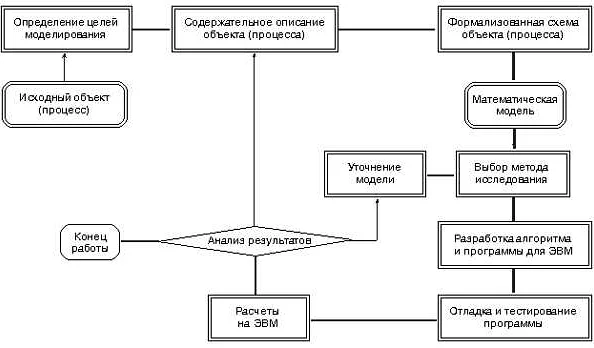
Математическое моделирование позволяет ученым формализовать проблему и выразить ее в виде математических уравнений или неравенств. Затем эти уравнения решаются с использованием различных методов, таких как численные методы или аналитические методы. Полученные результаты позволяют ученым делать выводы о поведении системы и предсказывать ее будущие состояния.
Одной из основных целей математического моделирования в научных исследованиях является поиск истины. Математические модели позволяют ученым проверять гипотезы и делать выводы на основе математических доказательств. Это позволяет ученым получать новые знания и расширять свою область исследований.
Еще одной важной целью математического моделирования является прогнозирование. Ученые используют математические модели для предсказания будущих состояний системы или для оценки вероятности различных событий. Это позволяет принимать более обоснованные решения и планировать действия на основе предсказанных результатов.
Оптимизация также является важной целью математического моделирования. Ученые исследуют различные параметры и варианты системы, чтобы найти оптимальные решения или стратегии. Математические модели позволяют ученым проводить различные эксперименты и анализировать результаты, чтобы найти наилучшие варианты и оптимизировать систему.
В заключение, математическое моделирование играет важную роль в научных исследованиях. Оно позволяет ученым исследовать сложные системы и явления, анализировать и предсказывать их поведение, а также находить оптимальные решения. Математическое моделирование помогает достичь целей истинности, прогнозирования и оптимизации в научных исследованиях.
Применение математических моделей в физике и химии
Математические модели имеют широкое применение в физике и химии. Они позволяют ученым лучше понять и объяснить физические и химические процессы, предсказывать результаты экспериментов и оптимизировать различные системы.
В физике математические модели используются для описания физических явлений, таких как движение тел, электромагнитные поля, взаимодействие частиц и т.д. Они позволяют ученым вывести уравнения, которые описывают эти явления и позволяют делать прогнозы о их поведении в различных условиях. Например, модели Максвелла описывают электромагнитные поля и позволяют предсказывать их взаимодействие с различными материалами.
В химии математические модели применяются для изучения химических реакций, кинетики и равновесия химических систем. Они позволяют ученым оптимизировать процессы синтеза новых веществ, предсказывать их свойства и влияние на окружающую среду. Например, модель Кинетической теории Больцмана описывает движение молекул в газе и позволяет предсказать термодинамические свойства газовых смесей.
Применение математических моделей в физике и химии позволяет ученым проводить виртуальные эксперименты, которые могут быть невозможны или слишком дороги в реальности. Они также позволяют экономить время и ресурсы при исследовании различных систем. Благодаря математическим моделям ученые могут предсказывать результаты своих исследований и принимать обоснованные решения на основе полученных данных.
Таким образом, математические модели играют важную роль в физике и химии, помогая ученым понять сложные физические и химические процессы, предсказать результаты экспериментов и оптимизировать различные системы. Их применение позволяет сделать науку более точной, эффективной и практичной.
Математическое моделирование в экономике и финансах
Математическое моделирование играет важную роль в экономике и финансах, позволяя анализировать и прогнозировать различные экономические и финансовые процессы. Оно основано на применении математических методов и инструментов для описания, анализа и оптимизации экономических систем.
Одной из основных задач математического моделирования в экономике и финансах является прогнозирование. Математические модели позволяют строить прогнозы различных показателей, таких как цены на товары, инфляция, доходность акций и другие финансовые показатели. Это позволяет принимать обоснованные решения и планировать долгосрочные стратегии в экономической и финансовой деятельности.
Еще одной важной задачей математического моделирования в экономике и финансах является оптимизация. Математические модели позволяют оптимизировать различные экономические и финансовые процессы, например, оптимизировать распределение ресурсов, максимизировать прибыль, минимизировать затраты и т.д. Это позволяет эффективно управлять экономическими и финансовыми ресурсами и достигать желаемых результатов.
Математическое моделирование в экономике и финансах также позволяет проводить анализ и исследования различных экономических и финансовых явлений. Математические модели позволяют анализировать взаимосвязи между различными переменными, выявлять закономерности и причинно-следственные связи. Это позволяет более глубоко понять и объяснить экономические и финансовые явления, а также предложить различные стратегии и политики для их улучшения.
Преимущества математического моделирования в экономике и финансах:Примеры применения
| Позволяет проводить точный анализ и прогнозирование экономических и финансовых процессов | Прогнозирование цен на товары, прогнозирование рыночной конъюнктуры |
| Позволяет оптимизировать экономические и финансовые процессы | Оптимизация портфеля инвестиций, оптимизация распределения ресурсов |
| Позволяет проводить анализ и исследования экономических и финансовых явлений | Анализ взаимосвязей между переменными, выявление закономерностей |
Таким образом, математическое моделирование является важным инструментом для анализа, прогнозирования и оптимизации экономических и финансовых процессов. Оно позволяет более глубоко понять и объяснить экономические и финансовые явления, а также принимать обоснованные решения и планировать долгосрочные стратегии в экономической и финансовой деятельности.
Математическое моделирование в медицине и биологии

В медицине математическое моделирование активно применяется для исследования различных заболеваний и их динамики, прогнозирования эффективности лечения, оптимизации дозировок лекарственных препаратов и разработки новых методов диагностики. Математические модели позволяют смоделировать и проанализировать различные процессы, такие как диффузия лекарственных веществ в организме, рост и развитие опухолей, электрическая активность сердца и мозга, популяционную динамику инфекционных заболеваний и многое другое.
В биологии математическое моделирование позволяет исследовать сложные биологические системы, такие как генетические сети, клеточные процессы, развитие и эволюция организмов. Моделирование позволяет увидеть, как различные факторы взаимодействуют внутри системы и как изменения одного параметра могут влиять на всю систему в целом. Математические модели позволяют проводить виртуальные эксперименты, которые помогают понять основные принципы функционирования и развития биологических систем.
Математическое моделирование в медицине и биологии играет важную роль в развитии новых методов исследования и лечения, а также в повышении эффективности существующих методов. Оно позволяет проводить более глубокий анализ и предсказание результатов, что помогает улучшить диагностику, предупредить возможные осложнения и выбрать наиболее эффективное лечение. Благодаря математическому моделированию ученые и врачи могут получить новые знания, которые помогут бороться с болезнями и улучшить качество жизни людей.


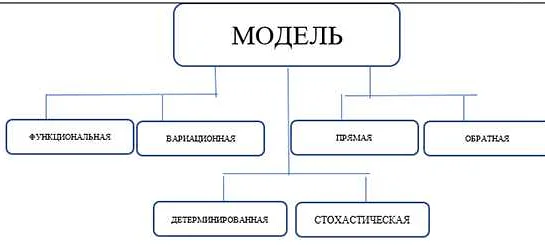

Математика — это не просто набор формул и алгоритмов, это наука, которая позволяет нам понять и объяснить мир вокруг нас. Главная цель моделирования в математике — найти истину. Математические модели помогают нам описывать и предсказывать различные явления, от движения планет до поведения финансовых рынков. Благодаря моделированию мы можем лучше понять и предсказать развитие событий и принимать обоснованные решения. Еще одна важная цель — оптимизация. Математические модели помогают нам найти оптимальные решения в различных областях, от логистики до экономики. Все это делает математику незаменимым инструментом для научных исследований и принятия обоснованных решений в различных сферах жизни.
Статья очень интересная и актуальная. Моделирование математики является важной научной дисциплиной, позволяющей нам понять и описать сложные явления в нашем мире. Целью такого моделирования является не только поиск истины, но и прогнозирование будущих событий, а также оптимизация процессов и решение различных задач. Математические модели помогают нам предсказывать поведение физических систем, структуры ДНК, экономические тренды и многое другое. Благодаря моделированию математики мы можем лучше понимать наш мир и принимать взвешенные решения на основе фактов и данных. Таким образом, моделирование математики играет важную роль в нашей жизни и помогает нам справиться с сложными задачами. Я очень рада, что существует такая наука, и надеюсь, что ее развитие будет продолжаться и в будущем.