Что такое математические основы информатики

Математические основы информатики — это основные математические концепции и методы, которые лежат в основе компьютерных наук и информационных технологий. В этой статье мы рассмотрим ключевые понятия, такие как алгоритмы, логика, теория графов и теория вероятностей, и объясним, как они связаны с информатикой и программированием.

Информатика — это наука о методах обработки информации, развивающаяся совместно с развитием компьютерных технологий. Однако, за основу информатики были взяты математические принципы и понятия. Математика играет важную роль в понимании и применении информатики, так как она предоставляет инструменты для анализа и описания данных, алгоритмов и структур данных.

В теории информатики математические основы используются для моделирования и формализации информационных процессов с помощью математических объектов, таких как графы, множества и логические выражения. Математика также помогает анализировать и оптимизировать алгоритмы, что позволяет создавать эффективные программы и системы.

Алгоритмы — это последовательность инструкций, определенных математически, которые решают определенную задачу. Они образуют основу для программирования и разработки компьютерных систем.

Математические основы информатики также применяются в криптографии для защиты информации. Криптографические алгоритмы основаны на математических принципах, таких как модулярная арифметика и теория чисел, и используются для шифрования данных и аутентификации.

Таким образом, понимание и применение математических основ информатики играют важную роль в разработке компьютерных систем, программировании и защите информации. Они позволяют создавать эффективные и безопасные решения, а также анализировать сложные информационные процессы. Без математических основ информатики невозможно представить себе современный мир информационных технологий.

Роль математики в информатике

Одной из главных областей, где математика играет ключевую роль, является разработка алгоритмов. Алгоритмы — это последовательность математических шагов, которые позволяют решать различные задачи. Математические концепции, такие как логика, алгебра и теория чисел, помогают разработчикам создавать эффективные и оптимизированные алгоритмы.

В структурах данных также широко используются математические принципы. Структуры данных — это способы организации и хранения данных в компьютере. Математическое понимание таких концепций, как графы, деревья и матрицы, позволяет разработчикам создавать эффективные и удобные структуры данных.

Теория графов — это еще одна область, где математика играет важную роль. Графы представляют собой совокупность вершин и ребер, которые используются для моделирования и анализа различных систем. Математические методы, такие как теория графов и алгебраические графы, позволяют решать широкий спектр задач, связанных с графами, например, поиск кратчайшего пути или определение связности.

Криптография — это область информатики, посвященная защите информации и обеспечению конфиденциальности. Математические методы, такие как теория чисел и модулярная арифметика, используются в криптографии для разработки алгоритмов шифрования и дешифрования. Математическая сложность некоторых задач помогает обеспечить безопасность информации и защитить данные от несанкционированного доступа.

Таким образом, математика играет важную роль в информатике, предоставляя основы для разработки алгоритмов, структур данных, анализа графов и криптографии. Понимание математических концепций и применение математических методов помогают информатикам создавать эффективные и надежные системы, обеспечивая безопасность и оптимизацию работы компьютерных систем.

Основные математические понятия в информатике

Математические понятия играют важную роль в информатике. Они обеспечивают основу для разработки алгоритмов, моделирования данных и решения различных задач.

Одно из ключевых понятий — это число. Числа используются для представления количественной информации. В информатике используются различные типы чисел, такие как целые числа, вещественные числа и комплексные числа.

Другое важное понятие — это операция. Операции позволяют производить различные действия над числами. В информатике наиболее часто используются операции сложения, вычитания, умножения и деления.

Также в информатике широко применяются понятия переменной и функции. Переменные используются для хранения значений, а функции позволяют выполнять определенные действия над этими значениями.

Для организации и структурирования данных в информатике используется структура данных. Структуры данных позволяют хранить и обрабатывать большие объемы информации эффективным и удобным способом. Одной из наиболее распространенных структур данных является таблица, которая представляет собой двумерный массив.

Также в информатике важным понятием является алгоритм. Алгоритм представляет собой последовательность шагов, которые позволяют решить определенную задачу. Алгоритмы используются для решения различных задач, таких как сортировка данных, поиск информации и т. д.

В заключение, математические понятия являются основой для разработки и применения информатики. Они позволяют представлять и обрабатывать информацию, разрабатывать алгоритмы и решать различные задачи. Понимание основных математических понятий в информатике является важным для успешной работы в этой области.

Теория множеств и ее применение

Множество в математике представляет собой совокупность элементов, которые мы рассматриваем как единое целое. Операции над множествами включают объединение, пересечение, разность и дополнение. Теория множеств также изучает отношения и функции между множествами.

В информатике теория множеств играет важную роль. Множества могут быть использованы для моделирования различных структур данных, таких как списки, графы и деревья. Операции над множествами могут быть использованы для фильтрации, сортировки и поиска данных. Множества также позволяют определить логические операции, такие как логическое И, ИЛИ и отрицание.

При разработке алгоритмов и программ теория множеств может использоваться для оптимизации процесса обработки данных. Например, при поиске дубликатов в больших наборах данных можно использовать операции пересечения и разности множеств для выявления повторяющихся элементов.

Теория множеств также применяется в теории формальных языков и автоматов. Множества символов могут быть использованы для определения алфавита, а множества строк — для определения языка. Операции над множествами строк могут быть использованы для проверки вхождения строки в язык или для генерации всех возможных комбинаций символов.

Таким образом, теория множеств играет важную роль в информатике и предоставляет мощный инструментарий для моделирования, обработки и анализа данных.

Дискретные структуры данных

Дискретные структуры данных играют важную роль в информатике. Они позволяют представлять и организовывать информацию в компьютерных системах.

Одним из основных примеров дискретных структур данных является таблица. Таблица представляет собой набор строк и столбцов, где каждая ячейка содержит определенное значение. Таблицы широко используются в базах данных и электронных таблицах.

Еще одной распространенной дискретной структурой данных является граф. Граф представляет собой совокупность вершин и ребер, которые соединяют эти вершины. Графы используются, например, для моделирования сетей, социальных связей и дорожных карт.

Другим примером дискретной структуры данных является дерево. Дерево состоит из узлов и ребер, где каждый узел имеет ровно одного родителя, за исключением корневого узла. Деревья широко применяются в информатике, включая структуры данных такие как бинарные деревья и синтаксические деревья.

Дискретные структуры данных играют важную роль в алгоритмах и программировании. Для эффективной обработки и анализа данных необходимо выбрать подходящую дискретную структуру данных, учитывая свойства и требования задачи.

Структура данныхОписаниеПримеры применения

Таблица	Набор строк и столбцов с ячейками, содержащими значения	Базы данных, электронные таблицы
Граф	Совокупность вершин и ребер	Моделирование сетей, социальных связей, дорожных карт
Дерево	Совокупность узлов и ребер с определенной иерархией	Бинарные деревья, синтаксические деревья

Алгоритмы и их математическая основа

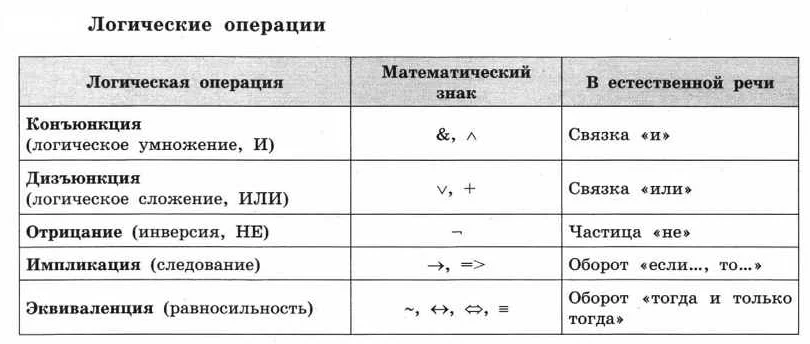
Математические основы алгоритмов включают в себя такие понятия, как логика, алгебра, теория графов и вероятность. Логика позволяет формулировать условия и правила, которым должны удовлетворять данные и операции, выполняемые алгоритмом. Алгебра предоставляет инструменты для работы с числами, переменными и операциями над ними.

Теория графов является одной из ключевых математических основ алгоритмов. Она изучает свойства и структуру графов, которые широко используются для моделирования различных задач. Алгоритмы на основе теории графов позволяют находить кратчайшие пути, оптимальные расписания и многое другое.

Вероятность и статистика также являются важной математической основой алгоритмов. Они позволяют учитывать случайные факторы и прогнозировать вероятность различных событий. Алгоритмы, основанные на вероятностных моделях, используются в статистике, машинном обучении и других областях, где важна оценка рисков и прогнозирование результатов.

Изучение и применение математических основ алгоритмов позволяет разработчикам создавать эффективные и надежные программы. Они позволяют оптимизировать процессы, решать сложные задачи и улучшать качество работы систем. Понимание математических основ алгоритмов является неотъемлемой частью образования в области информатики и помогает развивать аналитическое мышление и творческий подход к решению задач.

Теория вероятности и статистика в информатике

Теория вероятности изучает случайные события и их вероятности. В информатике она применяется, например, при моделировании случайных процессов, разработке алгоритмов случайных чисел и оценке вероятностей в задачах принятия решений.

Статистика, в свою очередь, занимается сбором, анализом и интерпретацией данных. В информатике статистика играет важную роль при обработке больших объемов данных, прогнозировании, машинном обучении и создании алгоритмов классификации.

Основные понятия теории вероятности, такие как вероятность события, условная вероятность и независимость событий, позволяют оценивать вероятности различных исходов и принимать взвешенные решения.

Статистика предоставляет инструменты для анализа данных, включая среднее значение, медиану, дисперсию и корреляцию. Они позволяют описывать данные и выявлять закономерности и связи между ними.

Использование теории вероятности и статистики в информатике позволяет решать задачи принятия решений, оптимизации алгоритмов, анализа данных и прогнозирования. Они являются неотъемлемой частью инструментария информатика и позволяют получать более точные и надежные результаты.

Математическая логика и формальные языки

Одним из основных понятий математической логики является понятие формулы. Формула представляет собой выражение, состоящее из символов и операций, которое может быть истинным или ложным в зависимости от значений переменных. Формулы могут быть построены с использованием логических операций, таких как конъюнкция, дизъюнкция, отрицание и импликация.

Формальные языки предназначены для описания структуры и семантики информации. Они состоят из алфавита, множества символов, и правил, определяющих, какие последовательности символов являются валидными выражениями. Формальные языки используются для описания программирования, командных языков, языков запросов к базам данных и других областей информатики.

Формальные языки могут быть классифицированы по различным критериям, таким как контекстно-свободные языки, регулярные языки, формальные грамматики и т.д. Каждый класс формальных языков имеет свои особенности и ограничения в использовании.

Математическая логика и формальные языки играют важную роль в информатике, так как они позволяют формализовать и структурировать информацию, а также разрабатывать алгоритмы и программы для обработки данных. Изучение математической логики и формальных языков является неотъемлемой частью образования в области информатики.

Линейная алгебра и ее роль в информатике

Линейная алгебра широко используется в компьютерной графике, машинном обучении, криптографии и других областях информатики. Она предоставляет инструменты для анализа и решения задач, связанных с линейными системами уравнений, векторами, матрицами и преобразованиями координат.

В компьютерной графике линейная алгебра используется для работы с трехмерными объектами, их поворотами, масштабированием и проекциями. Она позволяет создавать реалистичные модели и эффекты, а также обрабатывать и визуализировать данные.

В машинном обучении линейная алгебра используется для работы с матрицами и векторами, которые представляют данные и параметры моделей. Она позволяет выполнять операции над данными, такие как умножение матриц, решение систем уравнений и вычисление собственных значений.

В криптографии линейная алгебра применяется для защиты информации путем шифрования и дешифрования. Она помогает разрабатывать и анализировать криптографические алгоритмы, основанные на матричных операциях и линейных преобразованиях.

Таким образом, линейная алгебра играет важную роль в информатике, предоставляя математический аппарат и инструменты для решения различных задач. Понимание основных понятий и методов линейной алгебры является необходимым для успешного применения информатических решений в различных областях.

Вопрос-ответ:

Что такое математические основы информатики?

Математические основы информатики — это раздел математики, который изучает основные понятия, методы и модели, используемые в информатике. Они включают в себя такие области математики, как дискретная математика, математическая логика, теория множеств и теория графов.

Какие практические применения имеют математические основы информатики?

Математические основы информатики имеют широкий спектр практических применений. Они используются в разработке алгоритмов, программировании, криптографии, искусственном интеллекте, компьютерной графике и многих других областях информатики. Без математических основ информатики невозможно решать сложные задачи в области компьютерных наук.

Какие основные понятия изучаются в дискретной математике?

В дискретной математике изучаются такие понятия, как множества, отношения, функции, комбинаторика, теория графов и логика. Эти понятия играют важную роль в различных областях информатики, например, при решении задач поиска, сортировки, оптимизации и других.

Какие методы используются в математической логике?

Математическая логика использует такие методы, как символическая логика и формальные системы. Символическая логика изучает формальные языки и правила вывода, которые позволяют строить математические доказательства и рассуждения. Формальные системы представляют собой набор аксиом и правил вывода, которые используются для формализации математических теорий и построения математических моделей.

Какие задачи можно решать с помощью теории графов?

С помощью теории графов можно решать различные задачи, связанные с сетями, маршрутизацией, планированием и оптимизацией. Например, с ее помощью можно найти кратчайший путь между двумя вершинами в графе, определить наименьшее остовное дерево или решить задачу коммивояжера.

Какие математические основы лежат в основе информатики?

Математические основы информатики включают в себя такие разделы математики, как логика, теория множеств, алгебра, графы и теория вероятностей. Эти разделы математики используются для анализа и решения задач, связанных с обработкой информации и программированием.

Какие применения имеют математические основы информатики?

Математические основы информатики имеют широкий спектр применений. Они используются для разработки и анализа алгоритмов, построения и оптимизации дискретных моделей, создания и анализа сетей, решения задач оптимизации, а также для разработки криптографических методов и анализа данных. Кроме того, математические основы информатики играют важную роль в разных областях информационных технологий, таких как искусственный интеллект, машинное обучение, компьютерное зрение и другие.

Видео по теме: