Что такое математический анализ в 10 классе
Содержимое
- 1 Что такое математический анализ в 10 классе
Математический анализ в 10 классе — это раздел математики, в котором изучаются основные понятия и методы математического анализа. Ученики узнают о пределах функций, производных и интегралах, а также о применении этих понятий в различных задачах. Изучение математического анализа помогает ученикам развить логическое мышление и аналитические навыки.
Математический анализ – одна из важнейших дисциплин, изучаемых в школе. В 10 классе учащиеся знакомятся с основными понятиями и методами математического анализа, которые позволяют решать сложные задачи и проводить анализ функций.
Основные понятия включают в себя такие термины, как функция, производная и интеграл. Функция – это зависимость одной переменной от другой. Производная – это показатель скорости изменения функции в каждой ее точке. Интеграл – это площадь, заключенная между кривой графика функции и осью абсцисс.
Для того чтобы успешно решать задачи по математическому анализу, необходимо уметь применять методы математического анализа. Один из них – это метод дифференцирования, который позволяет найти производную функции. Другой метод – это метод интегрирования, который позволяет найти интеграл функции. Знание этих методов позволяет учащимся решать различные задачи, например, определять максимумы и минимумы функций или вычислять площадь фигур.
Примеры задач по математическому анализу в 10 классе: определить производную функции, найти точки экстремума, вычислить определенный интеграл и т.д. Решение таких задач требует понимания основных понятий и применения методов математического анализа.
Математический анализ в 10 классе

Основные понятия, изучаемые в математическом анализе в 10 классе, включают:
- Предел функции. Ученики узнают, как определить предел функции и как его использовать для решения различных задач.
- Производная функции. В ходе изучения производной функции ученики научатся определять ее и использовать для анализа поведения функции.
- Интеграл функции. Ученики узнают, как определить интеграл функции и как его использовать для вычисления площади под графиком функции.
- Приложения математического анализа. В рамках этого раздела ученики изучат приложения математического анализа в различных областях, таких как физика, экономика и другие науки.
В процессе изучения математического анализа в 10 классе, ученики решают множество задач, которые помогают им закрепить полученные знания и навыки. Примеры задач могут включать нахождение пределов функций, определение производных функций, вычисление интегралов и решение прикладных задач.
Изучение математического анализа в 10 классе является важным шагом в формировании математической культуры учеников. Этот предмет позволяет им развить абстрактное мышление, умение анализировать и решать сложные задачи. Кроме того, математический анализ является основой для дальнейшего изучения более сложных математических дисциплин, таких как аналитическая геометрия и математический анализ в старших классах.
Видео по теме:
Основные понятия

Предел функции – это значение, к которому функция стремится при приближении аргумента к определенной точке.
Производная функции – это показатель ее изменения в определенной точке. Она позволяет найти угол наклона касательной к графику функции в этой точке.
Интеграл функции – это площадь, ограниченная графиком функции и осью абсцисс на определенном отрезке.
Для решения задач по математическому анализу необходимо уметь находить пределы функций, находить производные и интегралы, а также применять эти знания для анализа и решения различных задач.
Важным понятием в математическом анализе является также непрерывность функции. Функция называется непрерывной, если ее график не имеет разрывов и перепрыгиваний.
Математический анализ играет важную роль в физике, экономике, информатике и других науках, где требуется анализировать и описывать различные явления и процессы.
Арифметические операции
Сложение – это операция, при которой два или более числа складываются, чтобы получить сумму. Например, 2 + 3 = 5.
Вычитание – это операция, при которой из одного числа вычитается другое число, чтобы получить разность. Например, 5 — 2 = 3.
Умножение – это операция, при которой одно число умножается на другое число, чтобы получить произведение. Например, 2 * 3 = 6.
Деление – это операция, при которой одно число делится на другое число, чтобы получить частное. Например, 6 / 2 = 3.
При выполнении арифметических операций важно помнить о приоритете операций. В математике существует определенный порядок выполнения операций: сначала выполняются операции в скобках, затем умножение и деление, и наконец сложение и вычитание.
Например, в выражении 2 + 3 * 4, сначала выполняется умножение (3 * 4 = 12), а затем сложение (2 + 12 = 14). Если нужно изменить порядок выполнения операций, можно использовать скобки. Например, (2 + 3) * 4 = 20.
Знание арифметических операций и правила их выполнения позволяет решать различные задачи и вычислять значения выражений.
Геометрические фигуры

В математике мы изучаем различные геометрические фигуры и их свойства. Геометрические фигуры могут быть двумерными или трехмерными, и они имеют разные формы и размеры.
Одной из основных геометрических фигур является окружность. Окружность — это множество точек в плоскости, равноудаленных от определенной точки, называемой центром окружности. Окружность имеет свойства, такие как радиус (расстояние от центра до любой точки окружности) и диаметр (расстояние между двумя точками на окружности через ее центр).
Прямоугольник — это четырехугольник с прямыми углами. У прямоугольника есть две пары параллельных сторон и все углы равны 90 градусам. Прямоугольник имеет свойства, такие как длины сторон, площадь (произведение длин сторон) и периметр (сумма длин всех сторон).
Треугольник — это фигура с тремя сторонами и тремя углами. В зависимости от длин сторон и величины углов, треугольник может быть разных типов: прямоугольный (один из углов равен 90 градусам), остроугольный (все углы меньше 90 градусов) или тупоугольный (один из углов больше 90 градусов).
Круг — это множество точек в пространстве, равноудаленных от определенной точки, называемой центром круга. У круга есть радиус и диаметр, так же как у окружности в двумерном пространстве.
Квадрат — это четырехугольник с равными сторонами и прямыми углами. Квадрат имеет свойства, такие как длина стороны, площадь (квадрат длины стороны) и периметр (сумма длин всех сторон).
Это только несколько примеров геометрических фигур, которые мы изучаем в математическом анализе. Изучение свойств и применение этих фигур помогает нам понять и анализировать различные проблемы и вопросы в геометрии и других областях математики.
Функции и их свойства
Функции могут иметь различные свойства, которые позволяют изучать их поведение и связь с другими функциями:
1. Определение функции: функция f(x) называется определенной, если для любого значения x из области определения существует единственное значение функции.
2. Область определения функции: это множество значений аргумента x, для которых функция определена.
3. Значение функции: это результат вычисления функции для заданного значения аргумента.
4. График функции: это геометрическое представление функции на координатной плоскости. График функции показывает, как значения функции зависят от значений аргумента.
5. Четность функции: функция f(x) называется четной, если для любого значения x верно, что f(-x) = f(x), и функция называется нечетной, если для любого значения x верно, что f(-x) = -f(x).
6. Монотонность функции: функция f(x) называется монотонно возрастающей, если для любых двух значений x1 и x2 из области определения, таких что x1 < x2, выполняется неравенство f(x1) < f(x2). Функция называется монотонно убывающей, если для любых двух значений x1 и x2 из области определения, таких что x1 < x2, выполняется неравенство f(x1) > f(x2).
7. Периодичность функции: функция f(x) называется периодической, если для любого значения x и некоторого положительного числа p выполняется равенство f(x+p) = f(x).
Изучение свойств функций позволяет анализировать их поведение, находить значения функций в различных точках, а также строить графики функций и решать уравнения и неравенства, связанные с функциями.
Производная и ее применение
Производная функции может быть использована для решения различных задач. Во-первых, она позволяет найти точки экстремума функции — максимумы и минимумы. Для этого необходимо найти точки, в которых производная равна нулю или не существует. Эти точки могут быть использованы для оптимизации процессов в различных областях, например, в экономике или физике.
Во-вторых, производная может использоваться для аппроксимации функций. Касательная к графику функции в определенной точке совпадает с графиком производной в этой точке. Это свойство позволяет использовать производную для приближенных вычислений значений функции. Например, при решении задачи о движении материальной точки можно использовать производную для нахождения скорости или ускорения в каждый момент времени.
Также производная может использоваться для исследования графика функции на монотонность и выпуклость. Знак производной показывает, в какую сторону функция возрастает или убывает, а вторая производная позволяет определить выпуклость или вогнутость графика. Это свойство производной позволяет анализировать поведение функции и делать выводы о ее свойствах.
В заключение, производная является мощным инструментом математического анализа, который находит широкое применение в различных областях науки и техники. Она позволяет определить скорость изменения функции и использовать эту информацию для решения задач и анализа поведения функции.
Интеграл и его применение
Для нахождения интеграла используется процесс интегрирования. Существуют различные методы интегрирования, такие как методы замены переменных, интегрирование по частям и расщепление на простые дроби.
Интегралы широко применяются в различных областях науки и техники. Например, в физике интегралы используются для расчета площади под графиком зависимости величины от времени, для определения работы и энергии, а также для решения дифференциальных уравнений.
В экономике интегралы помогают рассчитать общую прибыль или потери компании, а также определить площадь под спросом или предложением на рынке. В биологии интегралы используются для моделирования популяционной динамики и оценки площади под кривой распределения вероятностей.
Интегралы также применяются в теории вероятностей, финансовой математике, медицине и других областях. Знание интегралов и их применения является важным элементом математической подготовки и позволяет решать разнообразные задачи, связанные с анализом данных и моделированием.
Важно помнить, что для корректного решения задач, связанных с интегралами, необходимо обладать хорошими навыками алгебры, геометрии и аналитической геометрии, а также понимать основные понятия и свойства функций.
Графики и их анализ
Анализ графика функции позволяет определить основные характеристики функции, такие как ее область определения, область значений, экстремумы, точки пересечения с осями координат и другие.
Одной из основных задач анализа графиков функций является определение наличия и местоположения экстремумов. Экстремумы – это точки, в которых функция достигает своих максимальных или минимальных значений.
Точки пересечения графика с осями координат также являются важными характеристиками функции. Если точка пересечения с осью OX имеет координаты (а,0), то она называется корнем функции, а значение а – корнем уравнения f(x) = 0.
Помимо этого, анализ графика функции позволяет определить возрастание или убывание функции на заданном интервале и определить интервалы, на которых функция принимает положительные или отрицательные значения.
Изучение графиков функций помогает понять и запомнить основные свойства и закономерности, которые они проявляют. Графики часто используются для иллюстрации математических концепций и решения задач различной сложности.
Примеры задач

Ниже приведены несколько примеров задач, которые могут встретиться в курсе математического анализа в 10 классе:
- Найти предел функции f(x) при x стремящемся к некоторому значению a.
- Найти производную функции f(x) в заданной точке x=a.
- Решить уравнение f(x) = 0 и найти корни функции f(x).
- Исследовать функцию f(x) на экстремумы и точки перегиба.
- Найти площадь фигуры, ограниченной графиком функции f(x) и координатными осями.
Это лишь некоторые примеры задач, с которыми можно столкнуться в курсе математического анализа в 10 классе. Каждая из них требует применения определенных методов и инструментов анализа функций. Для успешного решения задач необходимо уметь применять знания о пределах, производных, уравнениях и графиках функций.
Вопрос-ответ:
Какие основные понятия изучаются в математическом анализе в 10 классе?
В математическом анализе в 10 классе изучаются такие основные понятия, как функция, предел функции, производная и интеграл. Ученики узнают, как определять их значения и использовать их в решении задач.
Что такое функция в математическом анализе?
Функция в математическом анализе — это соответствие между двумя множествами, в котором каждому элементу одного множества ставится в соответствие элемент другого множества. Функция может быть задана формулой, графиком или таблицей значений.
Что такое предел функции и как его вычислять?
Предел функции — это значение, к которому стремится функция при приближении аргумента к определенной точке или бесконечности. Вычисление предела функции можно осуществить с помощью различных методов, таких как подстановка, арифметические свойства пределов или использование известных пределов базовых функций.
Какие задачи можно решать с помощью производных и интегралов?
С помощью производных и интегралов можно решать множество задач различной сложности. Например, производная функции позволяет найти скорость изменения ее значения в каждой точке, а интеграл функции может использоваться для вычисления площади под ее графиком или решения задач на определенный интеграл.

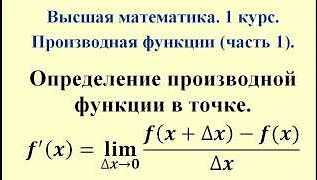


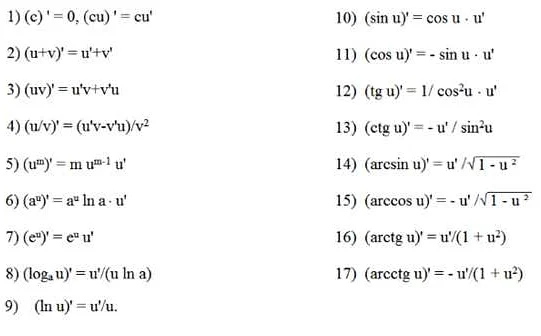
Статья очень полезная для родителей и учащихся. Математический анализ в 10 классе — это сложная и важная дисциплина, которая требует серьезного подхода. В статье хорошо разъяснены основные понятия и приведены примеры задач, с которыми можно столкнуться во время учебного процесса. Я нашла для себя много полезной информации и теперь лучше понимаю, какие навыки и знания мне необходимо приобрести. Было бы замечательно, если бы в статье было больше примеров и подробных объяснений решения задач. Тем не менее, я благодарна автору за его труд и рекомендую эту статью всем, кто хочет успешно освоить математический анализ в 10 классе.