Что такое d в математике производная
Содержимое
- 1 Что такое d в математике производная
- 1.1 Определение производной в математике
- 1.2 Принципы производной в математике
- 1.3 Важность производной в математике
- 1.4 Применение производной в математике
- 1.5 Точка экстремума в математике и производная
- 1.6 Правила нахождения производной в математике
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.9 Производная сложной функции в математике
- 1.10 Производная и график функции в математике
Производная в математике — это концепция, которая измеряет скорость изменения одной величины относительно другой. d обозначает дифференциал, который представляет собой малое изменение величины. Узнайте, как работает производная и как ее можно применять в различных областях математики и физики.
Производная является основным понятием математического анализа. Она позволяет определить скорость изменения функции в каждой точке ее области определения. Изучение производной играет важную роль в различных областях науки, включая физику, экономику, инженерию и многое другое.
Производная обозначается символом d и рассчитывается как предел отношения изменения функции к изменению ее аргумента, по мере приближения изменения к нулю. Она позволяет определить, насколько быстро функция меняется в данной точке и какие изменения могут произойти при небольшом изменении аргумента.
Производная функции может быть положительной, отрицательной или равной нулю. Если производная положительна, это означает, что функция возрастает в данной точке. Если производная отрицательна, то функция убывает. Если производная равна нулю, это может указывать на экстремум функции — максимум или минимум.
Изучение производной позволяет решать различные задачи, такие как определение точек экстремума функции, нахождение касательной к графику функции, анализ поведения функции и многое другое. Понимание производной d является важным элементом в освоении математического анализа и позволяет более глубоко понять исследуемые функции и их изменения.
Определение производной в математике
Формально, производная функции f(x) в точке x=a определяется как предел отношения изменения функции к изменению аргумента при стремлении изменения аргумента к нулю:
| d | f(x) |
| – | ––– |
| dx | dx |
Если этот предел существует, то он называется производной функции f(x) в точке x=a. Производная обозначается различными способами, например, d/dx(f(x)), f'(x), или dy/dx. Она позволяет нам понять, как ведет себя функция в каждой точке, и находит множество применений в различных областях математики и физики.
Принципы производной в математике
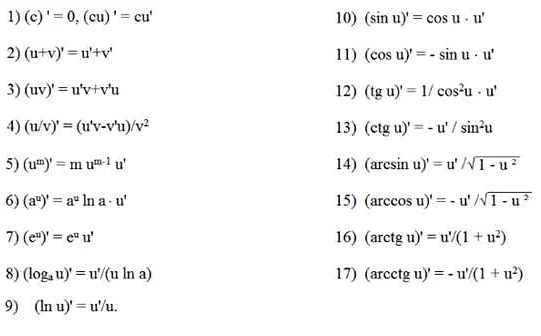
Существует несколько принципов, которыми руководствуются при работе с производными:
1. Принцип локальности: производная функции в точке характеризует ее поведение в этой точке. Она позволяет определить, является ли функция возрастающей или убывающей, а также найти точки экстремума.
2. Принцип линейности: производная суммы или разности функций равна сумме или разности их производных. То есть, если f(x) и g(x) — функции, их сумма или разность f(x) ± g(x) имеет производную, равную сумме или разности производных f'(x) ± g'(x).
3. Принцип дифференцирования сложной функции: если f(x) и g(x) — функции, и f(g(x)) — их композиция, то производная сложной функции равна произведению производной внешней функции f'(x) и производной внутренней функции g'(x).
4. Принцип дифференцирования произведения функций: производная произведения двух функций f(x) и g(x) равна сумме произведений первой функции на производную второй функции и второй функции на производную первой функции.
5. Принцип дифференцирования частного функций: производная частного двух функций f(x) и g(x) равна разности произведения производной первой функции на вторую функцию и произведения первой функции на производную второй функции, деленной на квадрат второй функции.
Знание данных принципов является основой для понимания и применения производных в математике. Они позволяют упростить вычисления и дать более полное представление о функциях и их свойствах.
Важность производной в математике
Производная функции в конкретной точке показывает, как быстро функция изменяется в этой точке. Это позволяет определить, например, экстремумы функции — точки, где функция принимает наибольшие или наименьшие значения, а также точки перегиба функции.
Производные также используются для решения различных задач в физике, экономике, статистике и других областях науки. Например, они позволяют определить скорость и ускорение движения тела, рост или падение цен на рынке, изменение показателей заболеваемости и многое другое.
Без производных многие математические модели и методы были бы непригодны для практического применения. Они позволяют упростить и анализировать сложные функции, описывающие реальные явления, и строить более точные прогнозы и модели.
Важность производной в математике несомненна, и она продолжает играть ключевую роль в различных областях знания. Понимание и применение производной позволяет углубиться в изучение математических закономерностей и найти решения сложных задач.
Применение производной в математике
Одной из главных областей, где используется производная, является оптимизация функций. Производная позволяет найти точки экстремума (минимума или максимума) функции, что позволяет оптимизировать процессы и решать различные задачи в экономике, физике, инженерии и других областях. Например, при оптимизации производственных процессов можно использовать производную для нахождения оптимальных значений параметров.
Также производная широко применяется в финансовой математике. Она помогает анализировать и моделировать финансовые рынки, определять риски и рентабельность инвестиций. Например, производная используется для определения моментов изменения тренда на финансовом рынке, а также для расчета граничных значений величин при определении стоимости опционов.
Еще одним примером применения производной является физика. Производная позволяет определить скорость изменения физической величины и связать ее с другими параметрами. Например, производная используется для определения скорости движения тела, ускорения, момента инерции и других характеристик.
Кроме того, производная играет важную роль в математическом моделировании. Она позволяет описывать изменение величин во времени и прогнозировать их поведение в будущем. Производная используется в моделях популяционной динамики, распространения эпидемий, а также в задачах управления трафиком, проектирования сооружений и других.
Таким образом, производная является мощным инструментом, который позволяет анализировать и оптимизировать различные процессы в различных областях знаний.
Точка экстремума в математике и производная

Чтобы найти точки экстремума функции с помощью производной, необходимо вычислить производную функции и найти ее корни. Для этого равняем производную функции нулю и решаем полученное уравнение. Корни данного уравнения будут значением аргумента, в которых функция имеет экстремумы.
Существуют два типа экстремумов: максимум и минимум. Если при переходе через экстремум функции меняет свой знак, то это будет точка максимума. Если же при переходе через экстремум знак функции не меняется, то это будет точка минимума.
Для вычисления точек экстремума функции с использованием производной, следует учесть следующие моменты:
- Если производная равна нулю, это может быть точкой экстремума, но не всегда.
- Производная может быть равна нулю в точке, где экстремума нет.
- Функция может иметь несколько экстремумов на одном интервале.
- Первая производная позволяет определить точки экстремума, но не дает информации о типе экстремума (максимум или минимум).
- Чтобы определить тип экстремума, необходимо анализировать вторую производную и проверять знаки.
Таким образом, производная функции позволяет находить точки экстремума и определять их типы. Это важный инструмент в математическом анализе, который позволяет исследовать поведение функций и находить оптимальные значения.
Правила нахождения производной в математике

- Правило линейности: производная линейной комбинации функций равна линейной комбинации производных этих функций. Если f(x) и g(x) являются дифференцируемыми функциями, а a и b — произвольными числами, то производная функции h(x) = a*f(x) + b*g(x) равна h'(x) = a*f'(x) + b*g'(x).
- Правило суммы и разности: производная суммы (или разности) двух функций равна сумме (или разности) их производных. Если f(x) и g(x) дифференцируемы, то производная функции h(x) = f(x) ± g(x) равна h'(x) = f'(x) ± g'(x).
- Правило произведения: производная произведения двух функций равна произведению производной первой функции на вторую и производной второй функции на первую. Если f(x) и g(x) дифференцируемы, то производная функции h(x) = f(x) * g(x) равна h'(x) = f'(x) * g(x) + f(x) * g'(x).
- Правило частного: производная частного двух функций равна разности произведения производной первой функции на вторую и произведения первой функции на производную второй, деленной на квадрат второй функции. Если f(x) и g(x) дифференцируемы и g(x) не равна нулю, то производная функции h(x) = f(x) / g(x) равна h'(x) = (f'(x) * g(x) — f(x) * g'(x)) / g(x)^2.
- Правило составной функции: производная составной функции равна произведению производной внешней функции на производную внутренней функции. Если y = f(u) и u = g(x) дифференцируемы, то производная функции y = f(g(x)) равна dy/dx = f'(g(x)) * g'(x).
Эти правила позволяют находить производные сложных функций и облегчают решение задач по дифференциальному исчислению. Они являются фундаментальными для изучения производных и находят широкое применение в различных областях математики и естественных наук.
Видео по теме:
Вопрос-ответ:
Что такое производная?
Производная — это одно из основных понятий математического анализа, которое позволяет изучать изменение функций в зависимости от изменения их аргумента. Фактически, производная функции в точке показывает, как быстро меняется значение функции при изменении аргумента в этой точке.
Как определить производную функции?
Для определения производной функции необходимо найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Этот предел и называется производной функции.
Как можно интерпретировать производную?
Производная функции в точке может быть интерпретирована как скорость изменения значения функции в этой точке. Если производная положительна, то функция возрастает, если отрицательна — убывает, а если равна нулю — функция имеет экстремум в данной точке.
Какие основные правила дифференцирования существуют?
Существует несколько основных правил дифференцирования. Например, правило суммы, которое гласит, что производная суммы двух функций равна сумме их производных. Также есть правило произведения, правило деления, правило дифференцирования сложной функции и другие.
Производная сложной функции в математике
Предположим, что у нас есть две функции: f(x) и g(x). Функция g(x) является внутренней функцией, а функция f(x) — внешней функцией. Для нахождения производной сложной функции необходимо применить правило дифференцирования, известное как правило дифференцирования сложной функции или правило цепной дифференциации.
Правило дифференцирования сложной функции утверждает, что производная сложной функции равна произведению производной внешней функции на производную внутренней функции. Формально, если y = f(g(x)), то производная сложной функции может быть записана как:
dy/dx = f'(g(x)) * g'(x)
Где f'(x) представляет собой производную внешней функции f(x), а g'(x) — производную внутренней функции g(x).
Производная сложной функции позволяет нам находить скорость изменения величины в зависимости от другой величины, когда они связаны через сложную функцию. Это очень полезно в различных областях, таких как физика, экономика и инженерия.
Производная и график функции в математике
График функции показывает зависимость значения функции от её аргумента. Производная функции может быть использована для анализа графика и определения особенностей функции.
Если производная функции положительна в какой-то точке, то это означает, что функция возрастает в этой точке. Если производная функции отрицательна в точке, то функция убывает. Если производная равна нулю, то функция имеет экстремум – максимум или минимум – в этой точке.
Также производная функции может помочь определить выпуклость или вогнутость графика функции. Если производная в точке положительна, то график функции выпуклый в этой точке. Если производная отрицательна, то график функции вогнутый. Производная равная нулю означает точку перегиба.
График функции и её производная могут быть использованы для определения точек экстремума, точек перегиба, а также для изучения областей возрастания и убывания функции.
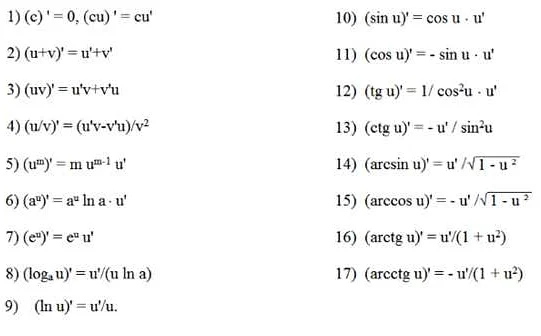



Производная d — это одно из самых важных понятий в математике. Она позволяет нам изучать изменение функции в каждой ее точке. Я уже давно слышал о производной, но никогда не понимал ее сути. Эта статья помогла мне разобраться в основных принципах ее вычисления. Оказывается, производная функции в точке — это предел отношения изменения функции к изменению аргумента при стремлении изменения аргумента к нулю. Понимание этого определения дало мне возможность лучше понять, как работает производная и как ее применять. Теперь я понимаю, что производная позволяет нам находить касательные к графикам функций, а также определять экстремумы функций. Я рад, что наконец-то разобрался с этой темой и могу применять производную в своих математических расчетах. Спасибо за полезную статью!
Производная d в математике — это мощный инструмент, позволяющий находить скорость изменения функции в каждой ее точке. Она помогает нам понять, как функция меняется с течением времени или в зависимости от других переменных. Производная позволяет нам вычислять наклон касательной к графику функции в определенной точке. Это особенно полезно при решении задач физики или экономики, где нам необходимо анализировать изменения величин. Благодаря производным мы можем оптимизировать функции, находить минимумы и максимумы, что является важным в различных практических сферах. В общем, производная — это неотъемлемая часть математики, которая помогает нам лучше понять и описать мир вокруг нас.
Производная в математике – это понятие, которое стало неразрывной частью моей жизни, как многим другим студентам. Она помогает нам понять, как функция меняется в каждой точке. Я всегда задаюсь вопросом, почему эта производная так важна? Какая связь между скоростью изменения функции и ее производной? Что делать, если у меня нет формулы для вычисления производной? Очень приятно осознавать, что математика всегда дает ответы на эти вопросы. Когда я понимаю, что производная функции в точке d(x) является скоростью изменения функции в этой точке, это дает мне ощущение контроля над миром чисел. Благодаря производной, я знаю, что функция может быть аппроксимирована линейной функцией в окрестности точки, и это помогает мне понять ее основные свойства. Так что, друзья, не бойтесь производной – она открывает перед нами мир возможностей и помогает нам разгадывать тайны математической гармонии.
Производная d в математике — это понятие, которое помогает нам изучать изменение функций и их скорость роста. Для меня, как для обычного читателя, понимание производной — это ключ к пониманию многих явлений в мире. Она позволяет определить, насколько быстро меняется функция в каждой ее точке. Кроме того, знание производной позволяет найти экстремумы функций, то есть точки, где функция достигает своих минимальных и максимальных значений. Это очень полезно при решении различных задач, как в физике, так и в экономике. Поэтому я считаю, что понимание производной — это важный инструмент, который помогает нам лучше понять и описать окружающий нас мир.
Статья очень понятно и доступно объясняет, что такое производная d в математике. Интересно узнать, что она является основным понятием математического анализа и используется для изучения изменений функций. Хорошо, что автор приводит примеры и пояснения, чтобы помочь нам лучше понять эту концепцию. Я научилась, что производная показывает скорость изменения функции в каждой точке и может быть интерпретирована как тангенс угла наклона касательной к графику функции. Было бы интересно узнать больше примеров использования производной в реальной жизни, чтобы лучше представить, как она применяется в практических задачах. В целом, статья дает хорошее введение в понятие производной и я рекомендую ее всем, кто хочет понять, как она работает.