Что называют математическим центром крестовины жд

Математический центр крестовины железнодорожной системы – это точка, которая является геометрическим центром пересечения всех линий путей. Этот центр играет важную роль в планировании и управлении движением поездов, обеспечивая оптимальное распределение ресурсов и максимальную эффективность перевозок.

Математический центр крестовины железной дороги — это понятие, которое используется в геометрии и инженерии для определения точки пересечения двух прямых, представляющих собой пути движения поездов. Эта точка часто называется истинным перекрестком, поскольку она является точкой идеального совпадения двух путей.

Математический центр крестовины железной дороги имеет особое значение для инженеров и архитекторов, занимающихся проектированием и строительством железнодорожных мостов, тоннелей и других инфраструктурных объектов. Он позволяет определить оптимальное расположение крестовины и обеспечивает безопасное и эффективное перемещение поездов.

Определение математического центра крестовины железной дороги основывается на принципах геометрии и алгебры. Используя уравнения двух прямых, представляющих пути движения поездов, можно найти точку их пересечения. Это позволяет определить координаты математического центра и его положение относительно других элементов железнодорожного строения.

Инженеры и архитекторы, работающие над проектами железнодорожных путей, должны учитывать математический центр крестовины железной дороги, чтобы обеспечить оптимальное функционирование и безопасность данного объекта. Он играет важную роль в проектировании и строительстве железнодорожной инфраструктуры, гарантируя эффективное перемещение поездов и минимизацию рисков.

Определение математического центра

Определение математического центра является важным для планирования строительства и обеспечения безопасности движения по железной дороге. Он позволяет определить точку, в которой находится равномерная нагрузка на ветки крестовины, что способствует более устойчивой конструкции и улучшению безопасности движения по железной дороге.

Роль математического центра в крестовине железной дороги

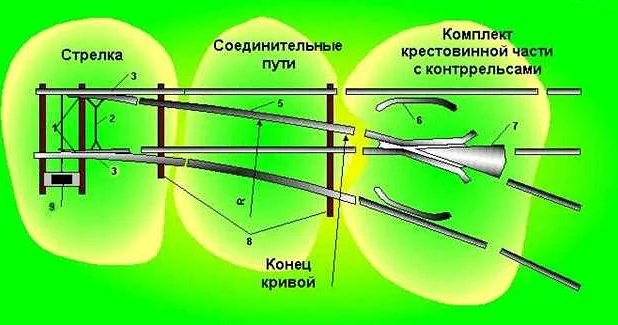
Математический центр определяется как точка пересечения осей железнодорожных путей, которая обеспечивает равенство расстояний до каждого из путей. Именно этот центр является опорным пунктом при установке крестовины, которая позволяет поездам переходить с одного пути на другой без изменения направления движения.

Роль математического центра состоит в том, чтобы обеспечить точность и надежность перемещения поездов на перекрестках железнодорожных путей. Благодаря правильному определению и установке математического центра, поезда могут безопасно и без задержек пересекать другие пути, соблюдая все правила и регламенты движения.

Поддержание правильной геометрии крестовины и точного положения математического центра играет важную роль в предотвращении аварийных ситуаций и обеспечении плавного движения поездов. В случае, если математический центр не установлен или установлен неправильно, это может привести к срыву поездов, обрушению железнодорожной инфраструктуры и серьезным авариям.

Таким образом, математический центр является неотъемлемой частью крестовины железной дороги, обеспечивающей безопасность и эффективность движения поездов. Его правильное определение и установка являются важными задачами, которые выполняются специалистами с учетом всех требований и нормативов.

Вычисление математического центра

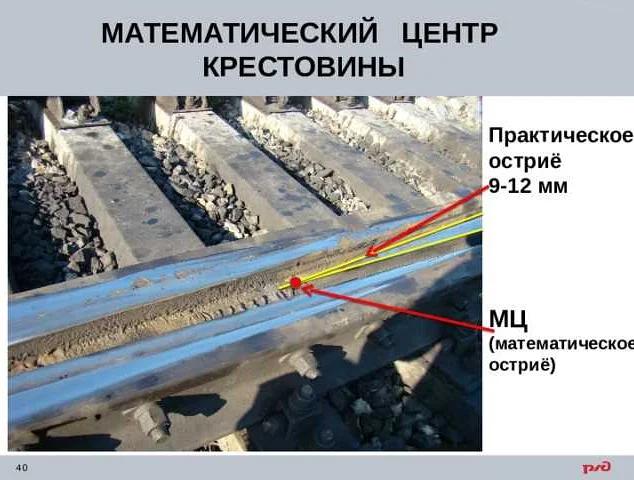
Для вычисления математического центра крестовины можно использовать следующую формулу:

УголКоординаты (x, y)

Верхний левый угол	(x1, y1)
Верхний правый угол	(x2, y2)
Нижний левый угол	(x3, y3)
Нижний правый угол	(x4, y4)

Для вычисления координат центра крестовины, необходимо найти среднее арифметическое значений координат x и y всех углов:

x_центр = (x1 + x2 + x3 + x4) / 4

y_центр = (y1 + y2 + y3 + y4) / 4

Таким образом, координаты точки, которая является математическим центром крестовины железной дороги, будут равны (x_центр, y_центр).

Применение математического центра в инженерии

В строительстве и архитектуре математический центр используется для определения равномерного распределения нагрузок и вычисления устойчивости конструкций. Он позволяет находить оптимальное расположение опор и точек закрепления, что обеспечивает прочность и безопасность зданий и сооружений.

В автомобильной промышленности математический центр используется для определения баланса и управляемости транспортных средств. Он помогает инженерам размещать двигатели, топливные баки и другие компоненты таким образом, чтобы достичь оптимального распределения массы и улучшить управляемость автомобиля.

В аэрокосмической инженерии математический центр используется для расчета положения центра тяжести и определения стабильности и маневренности космических аппаратов. Он позволяет инженерам размещать грузы, топливные баки и другие компоненты таким образом, чтобы обеспечить управляемость и безопасность полета.

В электротехнике математический центр используется для расчета электрических цепей и определения оптимального расположения компонентов. Он позволяет инженерам улучшать эффективность и надежность систем электроснабжения, а также оптимизировать распределение электрической энергии.

Таким образом, математический центр играет важную роль в инженерии, обеспечивая оптимизацию и улучшение различных систем и конструкций.

Значение математического центра для безопасности

Знание математического центра имеет большое значение для безопасности, поскольку позволяет точно определить положение каждой крестовины, а также расстояние между ней и другими элементами железнодорожного пути. Это позволяет предотвратить возможность столкновения поездов или других непредвиденных ситуаций.

Безопасность движения поездов является одним из основных приоритетов в железнодорожной индустрии. Правильное определение математического центра позволяет достичь высокого уровня безопасности и предотвратить возможные аварии и происшествия.

Кроме того, знание математического центра позволяет проводить регулярные проверки и обслуживание крестовин, что также является важным фактором безопасности. Регулярное обслуживание позволяет выявить и устранить возможные дефекты, такие как износ или повреждения, которые могут повлиять на безопасность движения поездов.

В целом, математический центр крестовины железной дороги играет важную роль в обеспечении безопасности движения поездов. Он позволяет точно определить положение и расстояние между элементами железнодорожного пути, а также проводить регулярное обслуживание и проверки, что способствует предотвращению возможных аварий и обеспечивает гладкое и безопасное движение поездов.

Инновационные методы определения математического центра

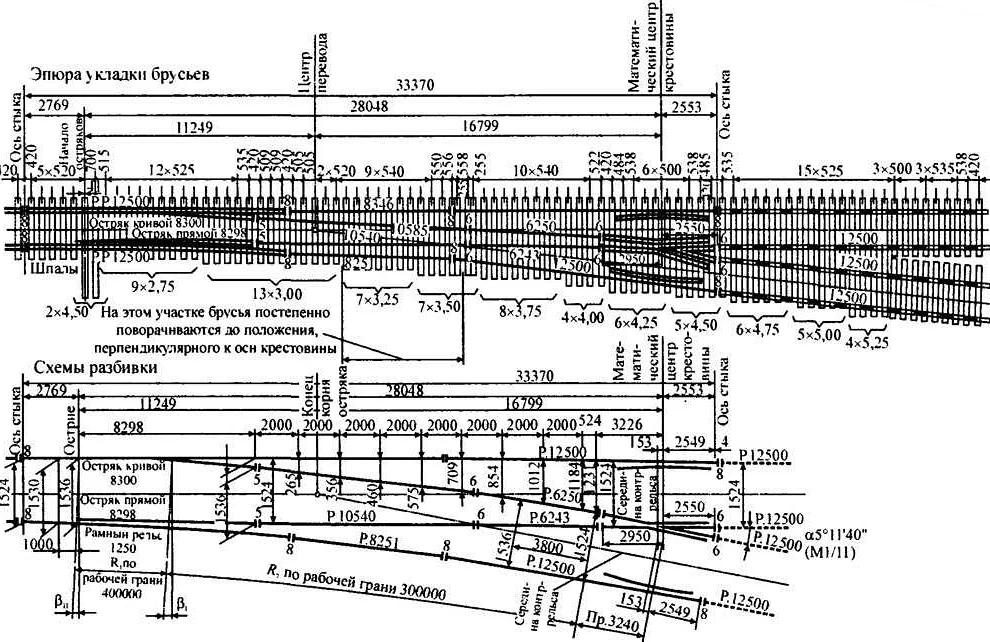
Существует несколько инновационных методов, которые позволяют определить математический центр крестовины железной дороги с высокой точностью.

Метод геометрического центра. Этот метод основан на простом геометрическом принципе: математический центр крестовины совпадает с точкой пересечения ее диагоналей. Для определения центра необходимо измерить длины диагоналей крестовины и найти их точку пересечения.

Метод центра тяжести. Данный метод основан на принципе равномерного распределения массы крестовины. Определение математического центра происходит путем нахождения точки, в которой сумма моментов относительно всех точек крестовины равна нулю.

Метод средних перпендикуляров. Этот метод основан на определении средних перпендикуляров к сторонам крестовины. Для этого измеряются длины сторон крестовины и находятся их середины. Затем проводятся перпендикуляры к сторонам, и их пересечение определяет математический центр.

Видео по теме:

Вопрос-ответ:

Что такое математический центр крестовины железной дороги?

Математический центр крестовины железной дороги — это точка, которая является геометрическим центром крестовины, образованной пересечением двух железнодорожных путей.

Зачем нужен математический центр крестовины железной дороги?

Математический центр крестовины железной дороги используется для определения радиуса кривой, на которой построена крестовина. Это позволяет обеспечить безопасное движение поездов на перекрестках железных дорог.

Как определить математический центр крестовины железной дороги?

Математический центр крестовины железной дороги определяется с использованием методов геометрии. Для этого необходимо знать координаты начала и конца каждого железнодорожного пути, а также угол пересечения путей.

Какие параметры учитываются при определении математического центра крестовины железной дороги?

При определении математического центра крестовины железной дороги учитываются параметры, такие как угол пересечения путей, радиусы кривизны путей, длина и ширина крестовины.

Какие преимущества дает знание математического центра крестовины железной дороги?

Знание математического центра крестовины железной дороги позволяет установить правильные параметры крестовины, что способствует безопасному и эффективному движению поездов на перекрестках железных дорог. Это также позволяет оптимизировать строительство и развитие железнодорожных путей.

Примеры использования математического центра в железнодорожной инфраструктуре

1. Оптимальное размещение остановок и станций. Математический центр может быть использован для определения наиболее выгодных мест расположения остановок и станций на железнодорожной линии с учетом пассажиропотока, географических особенностей и других факторов.
2. Планирование грузоперевозок. Математический центр помогает оптимизировать маршруты грузовых поездов, учитывая требования грузопотока, доступность пунктов погрузки и выгрузки, а также другие ограничения.
3. Управление движением поездов. Математический центр используется для прогнозирования и планирования движения поездов, оптимизации времени прибытия и отправления, а также распределения поездов по путям и маршрутам.
4. Обслуживание и ремонт инфраструктуры. Математический центр помогает оптимизировать графики обслуживания и ремонта различных элементов железнодорожной инфраструктуры, таких как пути, сигнально-телематические системы, электрическое оборудование и др.

Это лишь некоторые примеры использования математического центра в железнодорожной инфраструктуре. Его применение может быть очень широким и варьироваться в зависимости от конкретных задач и требований.

Выводы: важность математического центра в проектировании крестовин железных дорог

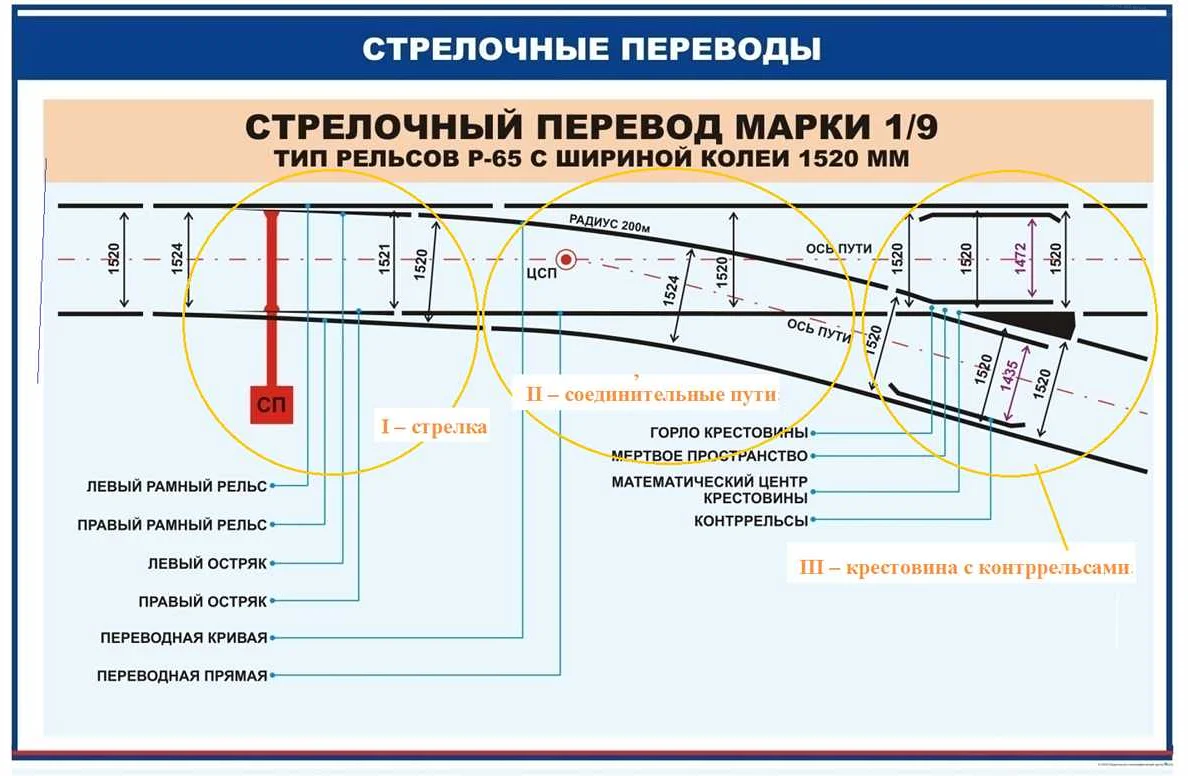
Важность математического центра заключается в обеспечении безопасности и эффективности движения поездов. Расположение всех элементов крестовины вокруг центральной точки обеспечивает равномерное распределение нагрузки и минимизирует риск возникновения аварийных ситуаций.

Математический расчет центра крестовины позволяет определить оптимальное положение элементов с учетом физической конфигурации местности и требований безопасности. Правильное размещение рельсов, стрелочных переводов и сигнальных устройств вокруг математического центра обеспечивает плавность и точность движения поездов, а также минимизирует износ и повреждения оборудования.

Отсутствие или неправильное определение математического центра может привести к серьезным проблемам, таким как дерайлменты, столкновения поездов и перегрузка некоторых участков крестовины. Поэтому, при проектировании и строительстве железнодорожных переездов, особое внимание должно уделяться вычислению и корректному размещению математического центра.

В целом, математический центр крестовины является фундаментальным элементом в проектировании железных дорог. Его правильное определение и размещение играют ключевую роль в обеспечении безопасности и эффективности движения поездов, а также в снижении износа и повреждений оборудования. Поэтому, проектировщики и инженеры должны обращать особое внимание на этот аспект при создании и модернизации железнодорожных переездов.