Что называют математическим центром крестовины

Математический центр крестовины – это точка пересечения диагоналей крестовины, которая имеет важное значение в геометрии и вычислительной геометрии. Узнайте, как определить и использовать математический центр крестовины в своих расчетах и конструкциях.

Математический центр крестовины — это точка, которая является центром масс системы из четырех пересекающихся прямых линий, образующих крестовину. Этот центр имеет важное значение в механике и статике, так как позволяет определить равновесие системы и точку приложения силы, которая не вызывает вращательного момента.

Рассчитать математический центр крестовины можно, используя геометрические методы. Для этого необходимо знать координаты точек пересечения прямых линий. Затем, с помощью формулы, которая основана на принципе равенства моментов, можно найти координаты математического центра крестовины.

Формула для расчета математического центра крестовины имеет вид:

x = (x1 + x2 + x3 + x4) / 4,

y = (y1 + y2 + y3 + y4) / 4,

где x1, x2, x3, x4 — координаты точек пересечения по горизонтали, а y1, y2, y3, y4 — координаты точек пересечения по вертикали.

Расчет математического центра крестовины позволяет установить точку, вокруг которой можно считать вращение системы равномерным и безопасным.

Определение математического центра крестовины

Для определения математического центра крестовины необходимо знать координаты его точек. Если крестовина имеет четыре точки с координатами (x1, y1), (x2, y2), (x3, y3) и (x4, y4), то координаты математического центра можно рассчитать по следующим формулам:

• x = (x1 + x2 + x3 + x4) / 4
• y = (y1 + y2 + y3 + y4) / 4

Таким образом, математический центр крестовины будет иметь координаты (x, y).

Определение математического центра крестовины является важным для различных математических расчетов и конструкций, связанных с этой геометрической фигурой. Например, при проектировании зданий или механизмов можно использовать математический центр крестовины для распределения нагрузок и обеспечения равновесия.

Формула для расчета математического центра крестовины

Пусть дана крестовина с вертикальной и горизонтальной осью симметрии, и имеются координаты ее вершин:

ВершинаКоордината XКоордината Y

A	xA	yA
B	xB	yB
C	xC	yC
D	xD	yD

Тогда координаты математического центра крестовины (Xc, Yc) могут быть рассчитаны следующим образом:

Xc = (xA + xB + xC + xD) / 4

Yc = (yA + yB + yC + yD) / 4

Таким образом, используя данную формулу, мы можем рассчитать координаты математического центра крестовины, зная координаты ее вершин.

Пример расчета математического центра крестовины

Для расчета математического центра крестовины необходимо знать координаты каждой из точек, образующих крестовину. Рассмотрим пример расчета на простом двумерном пространстве.

Пусть у нас есть крестовина, состоящая из четырех точек:

• Точка A с координатами (xA, yA)
• Точка B с координатами (xB, yB)
• Точка C с координатами (xC, yC)
• Точка D с координатами (xD, yD)

Для расчета математического центра крестовины нужно найти среднее арифметическое значения координат по оси X и оси Y.

Формулы для расчета координат центра:

• Координата Xцентр = (xA + xB + xC + xD) / 4
• Координата Yцентр = (yA + yB + yC + yD) / 4

Таким образом, мы получим координаты математического центра крестовины.

В данном примере, если координаты точек A, B, C и D равны:

• A(2, 4)
• B(6, 4)
• C(6, 8)
• D(2, 8)

То координаты математического центра будут:

• Xцентр = (2 + 6 + 6 + 2) / 4 = 4
• Yцентр = (4 + 4 + 8 + 8) / 4 = 6

Таким образом, математический центр крестовины в данном примере будет иметь координаты (4, 6).

Значение математического центра крестовины

Значение математического центра крестовины имеет важное практическое значение. Оно используется в различных областях, таких как архитектура, дизайн и механика, для определения равновесия и стабильности структур.

Рассчитать математический центр крестовины можно путем нахождения среднего значения координат всех точек, которые образуют крестовину. Для простой крестовины, состоящей из двух пересекающихся линий, это можно сделать следующим образом:

1. Найдите суммы всех x-координат и всех y-координат всех точек крестовины.
2. Разделите каждую из этих сумм на количество точек крестовины.
3. Таким образом, получите среднее значение x-координат и y-координат.
4. Эти два значения будут координатами математического центра крестовины.

Зная значение математического центра крестовины, можно проводить различные расчеты и анализировать характеристики фигуры, такие как сила, момент инерции и устойчивость.

Применение математического центра крестовины

Применение математического центра крестовины широко используется в различных сферах, включая геодезию, строительство, топографию, архитектуру и дизайн.

В геодезии и топографии математический центр крестовины используется для определения точных координат опорных точек и их дальнейшего использования при замерах и построении карт.

В строительстве и архитектуре математический центр крестовины позволяет определить точку баланса и равномерно распределить нагрузку на конструкцию.

В дизайне математический центр крестовины используется для создания симметричных композиций и расположения основных элементов проекта.

Важно отметить, что математический центр крестовины является идеализированным понятием и может быть не всегда практически применим в реальной жизни. Однако, его понимание и учет способствуют точности и гармоничности работ, основанных на крестовине.

Сравнение математического центра крестовины с геометрическим центром

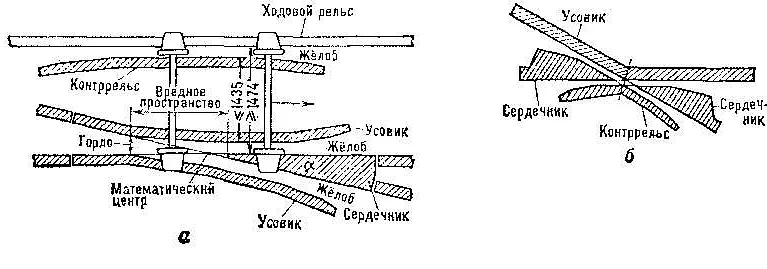
Геометрический центр – это точка, которая является пересечением диагоналей крестовины. Он представляет собой точку, которая находится на одинаковом расстоянии от всех концов крестовины. Геометрический центр является центром симметрии крестовины и может быть рассчитан с помощью геометрических формул.

Математический центр крестовины, с другой стороны, рассчитывается путем нахождения среднего значения координат всех точек крестовины. Он представляет собой точку, которая является средним положением всех точек крестовины. Математический центр может быть рассчитан с помощью алгебраических формул и обычно используется в математическом анализе или программировании.

Сравнивая эти два понятия, можно сказать, что математический центр крестовины точнее отражает среднюю точку крестовины, так как он учитывает все точки, а не только диагонали. Геометрический центр, с другой стороны, является более простым и легко вычисляемым способом определения средней точки крестовины.

Важно отметить, что в большинстве случаев математический центр и геометрический центр будут близки друг к другу и не будут сильно отличаться. Однако в некоторых сложных геометрических конструкциях разница между ними может быть значительной.

В конечном счете, выбор между использованием математического центра или геометрического центра зависит от конкретной задачи и требований к точности. Оба этих понятия имеют свои применения и позволяют описывать среднюю точку крестовины, каждый в своем контексте.

Вопрос-ответ:

Что такое математический центр крестовины?

Математический центр крестовины — это точка, которая является центром масс крестовины, представляющей собой пересечение двух перекрещивающихся плоских элементов. В математике и физике, центр масс представляет собой точку, в которой можно считать распределенную массу системы сосредоточенной.

Зачем нужно рассчитывать математический центр крестовины?

Расчет математического центра крестовины позволяет определить точку, в которой будет сосредоточена масса этой системы. Это важно, например, при проектировании конструкций, где необходимо учитывать равномерное распределение нагрузки или при работе с рычагами и механизмами, где необходимо определить оптимальную точку приложения силы.

Как рассчитать математический центр крестовины?

Рассчитать математический центр крестовины можно при помощи формулы. Для плоской крестовины, состоящей из двух перекрещивающихся прямых, центр крестовины будет являться серединной точкой отрезка, соединяющего середины этих прямых.

Какую формулу использовать для расчета математического центра крестовины?

Для расчета математического центра крестовины можно использовать формулу x = (x1 + x2) / 2 и y = (y1 + y2) / 2, где x1 и y1 — координаты середины одной прямой, x2 и y2 — координаты середины другой прямой.

Какие еще способы существуют для расчета математического центра крестовины?

Если крестовина имеет сложную форму, то расчет ее математического центра может быть более сложным. В таких случаях можно использовать методы интегралов или численного интегрирования для определения координат центра масс. Также можно воспользоваться специальными программами для компьютерного моделирования и расчета центра масс.

Особенности расчета математического центра крестовины

Расчет математического центра крестовины осуществляется на основе геометрических данных данной фигуры. Для простоты, будем рассматривать крестовину, состоящую из двух перпендикулярных перекрещивающихся балок равной ширины.

Для определения координат центра тяжести крестовины, необходимо разделить ее на две половины. Затем, для каждой половины, определить ось симметрии и рассчитать моменты инерции относительно этой оси.

Формула расчета момента инерции для прямоугольной балки имеет вид:

• Для горизонтальной балки: I = (b * h^3) / 12
• Для вертикальной балки: I = (h * b^3) / 12

Где I — момент инерции, b — ширина балки, h — высота балки.

После расчета моментов инерции для каждой половины крестовины, необходимо найти сумму этих моментов и разделить ее на общую площадь крестовины. Полученные значения представляют координаты математического центра крестовины.

Расчет математического центра крестовины является важным этапом проектирования и служит основой для определения равномерного распределения нагрузки и обеспечения стабильности конструкции.

Видео по теме: