Математический закон теории вероятности в чем выражается

Математический закон теории вероятности определяет вероятность наступления событий и их отношение к общему числу всех возможных исходов. Узнайте, как математический закон теории вероятности выражается и как он применяется в различных областях науки и жизни.

Теория вероятности — это раздел математики, который изучает случайные явления и их вероятности. Она является базовым инструментом для анализа и прогнозирования различных событий. Основой теории вероятности является математический закон, который определяет вероятность возникновения события. Этот закон позволяет количественно оценивать риск и принимать обоснованные решения.

Основные принципы математического закона теории вероятности включают в себя следующие: вероятность события лежит в интервале от 0 до 1, сумма вероятностей всех возможных исходов равна 1, вероятность объединения несовместных событий равна сумме их вероятностей и т.д. Эти принципы позволяют строить математическую модель для оценки вероятности конкретного события.

Применение математического закона теории вероятности весьма широко. Во-первых, он используется в статистике для анализа данных и выявления закономерностей. Во-вторых, он применяется в финансовой сфере для прогнозирования рыночных трендов и определения рисков. В-третьих, он находит применение в игорной индустрии для вычисления шансов на выигрыш. И это только некоторые примеры использования математического закона теории вероятности.

В заключение, математический закон теории вероятности является неотъемлемой частью нашей жизни. Он помогает нам принимать рациональные решения, предсказывать будущие события и анализировать данные. Понимание основных принципов и применение этого закона позволяют нам лучше понять и предугадать мир вокруг нас.

Вероятность и ее математический закон

Математический закон вероятности устанавливает основные принципы расчета и оценки вероятностей. Он основан на трех основных аксиомах:

1. Вероятность события всегда положительна и не превышает единицы: 0 ≤ P(A) ≤ 1.
2. Вероятность достоверного события равна единице: P(Ω) = 1, где Ω — пространство элементарных исходов.
3. Если события A и B несовместны (не могут произойти одновременно), то вероятность их объединения равна сумме их вероятностей: P(A ∪ B) = P(A) + P(B).

Математический закон вероятности позволяет рассчитывать вероятности наступления различных событий, а также проводить различные статистические исследования. Он применяется во многих областях, таких как физика, экономика, медицина, социология и т. д.

Знание математического закона вероятности позволяет анализировать и прогнозировать случайные явления, определять их вероятности и принимать обоснованные решения на основе этих данных.

Основные принципы

• Принцип сложения вероятностей: гласит, что вероятность суммы двух несовместных событий равна сумме их вероятностей. Этот принцип позволяет вычислять вероятность появления различных исходов в случайных экспериментах.
• Принцип умножения вероятностей: утверждает, что вероятность одновременного наступления двух независимых событий равна произведению их вероятностей. Этот принцип помогает определить вероятность наступления сложных событий, состоящих из нескольких независимых частей.
• Принцип отрицания вероятностей: указывает на то, что вероятность противоположного события равна единице минус вероятность исходного события. Этот принцип позволяет находить вероятности событий, если известны вероятности их противоположных.

Основные принципы теории вероятности являются основой для множества математических моделей и методов, используемых в различных областях науки и практики. Их применение позволяет проводить анализ рисков, прогнозировать вероятности событий, определять отклонения от средних значений и многое другое.

Понятие случайной величины в теории вероятности

Случайная величина может быть дискретной или непрерывной. Дискретная случайная величина принимает конечное или счетное множество значений, например, количество выпавших орлов при броске монеты. Непрерывная случайная величина может принимать любое значение из определенного интервала, например, время, необходимое для достижения определенного пункта.

С использованием случайной величины можно определить вероятности различных событий. Например, вероятность того, что дискретная случайная величина примет определенное значение, или вероятность того, что непрерывная случайная величина попадет в определенный интервал значений.

Для работы с случайными величинами используются различные математические методы, включая функции распределения, математическое ожидание, дисперсию и другие. Эти методы позволяют анализировать и описывать случайные явления с помощью численных характеристик.

Понятие случайной величины является одним из основных принципов теории вероятности и широко применяется в различных областях, таких как статистика, физика, экономика и другие.

Аксиоматическая теория вероятности

Основные принципы аксиоматической теории вероятности включают:

1. Вероятностная функция должна быть неотрицательной. Для любого события вероятность не может быть меньше нуля.
2. Вероятностная функция должна быть ограниченной сверху. Для любого события вероятность не может превышать единицу.
3. Вероятность достоверного события (такого, которое обязательно произойдет) равна 1.
4. Вероятности несовместных событий (событий, которые не могут произойти одновременно) складываются. Для любого конечного набора несовместных событий вероятность их объединения равна сумме вероятностей каждого события.

Аксиоматическая теория вероятности предоставляет строгую математическую основу для работы с вероятностными событиями. Она позволяет формализовать вероятностные пространства и разработать методы для вычисления вероятностей различных событий. Это помогает в практических приложениях, таких как статистика, финансовые моделирование, машинное обучение и т. д.

Основные принципы комбинаторики

Один из основных принципов комбинаторики — принцип умножения. Он утверждает, что если задачу можно разбить на несколько независимых этапов, каждый из которых можно выполнить по нескольку способов, то общее количество способов выполнить всю задачу будет равно произведению количеств способов выполнить каждый отдельный этап.

Другим важным принципом комбинаторики является принцип сложения. Он применяется в случаях, когда задача разбивается на несколько взаимоисключающих подзадач, и решение каждой из них не влияет на решение других. В этом случае общее количество способов решить задачу будет равно сумме количеств способов решить каждую из подзадач.

Также существует принцип отрицания. Он позволяет решать задачи путем подсчета всех способов решить обратную задачу и затем вычитания этого количества из общего числа всех возможных вариантов.

Принцип комбинаторики имеет широкое применение в различных областях, таких как теория вероятностей, комбинаторный анализ, криптография и другие. Он позволяет решать задачи подсчета комбинаций и перестановок, а также применять их в практических задачах, таких как составление расписаний, решение задач на размещение и упаковку объектов, определение вероятностей различных событий и многое другое.

Название принципаОписание

Принцип умножения	Если задачу можно разбить на несколько независимых этапов, каждый из которых можно выполнить по нескольку способов, то общее количество способов выполнить всю задачу будет равно произведению количеств способов выполнить каждый отдельный этап.
Принцип сложения	Если задача разбивается на несколько взаимоисключающих подзадач, и решение каждой из них не влияет на решение других, то общее количество способов решить задачу будет равно сумме количеств способов решить каждую из подзадач.
Принцип отрицания	Позволяет решать задачи путем подсчета всех способов решить обратную задачу и затем вычитания этого количества из общего числа всех возможных вариантов.

Применение математического закона теории вероятности

Математический закон теории вероятности имеет широкое применение в различных областях науки и жизни. Он позволяет оценивать вероятность наступления событий, предсказывать и анализировать результаты экспериментов и случайных процессов.

Одним из основных применений закона вероятности является статистика. С помощью теории вероятности можно проводить статистические исследования, оценивать вероятность различных событий и их взаимосвязи. Например, вероятность того, что случайно выбранный человек будет правшой или левшой, может быть оценена с помощью закона вероятности.

Теория вероятности также применяется в физике и инженерии. Например, при расчете надежности технических систем или при моделировании случайных процессов в физике. Математический закон вероятности позволяет оценить вероятность отказа системы или предсказать результаты экспериментов с помощью статистических методов.

В экономике теория вероятности используется для анализа финансовых рынков, оценки вероятности прибыли или убытка, а также для принятия решений в условиях неопределенности. Математический закон вероятности позволяет оценить вероятность различных событий и выбрать наиболее оптимальную стратегию действий.

В медицине и биологии теория вероятности применяется для оценки эффективности лекарственных препаратов, анализа результатов медицинских исследований, а также для оценки риска развития различных заболеваний. Математический закон вероятности позволяет оценить вероятность того, что лекарственный препарат будет эффективным или что определенное заболевание может развиться.

Таким образом, математический закон теории вероятности является важным инструментом для анализа и прогнозирования различных событий и процессов. Он находит применение в различных областях науки и позволяет оценивать вероятность наступления событий, предсказывать результаты экспериментов и принимать рациональные решения.

Типы случайных величин и их распределения

Дискретные случайные величины принимают конечное или счетное количество значений. Примерами дискретных случайных величин могут служить количество выпадения определенной грани на игральной кости или количество клиентов, посетивших определенный магазин в течение дня. Дискретные случайные величины характеризуются функцией вероятности, которая определяет вероятность каждого возможного значения.

Непрерывные случайные величины могут принимать любое значение на некотором промежутке. Примерами непрерывных случайных величин являются рост человека, время ожидания на остановке или количество дождевых осадков в определенном районе. Непрерывные случайные величины характеризуются плотностью вероятности, которая показывает вероятность попадания случайной величины в определенный интервал значений.

Каждый тип случайных величин имеет свое распределение вероятностей. Для дискретных случайных величин это дискретное распределение, которое задается таблицей или графиком вероятностей для каждого значения. Для непрерывных случайных величин это непрерывное распределение, которое задается плотностью вероятности и может быть представлено графиком плотности вероятности.

Тип случайной величиныПримерыРаспределение вероятностей

Дискретная	Количество выпадения грани на игральной кости	Функция вероятности
Непрерывная	Рост человека	Плотность вероятности

Изучение типов случайных величин и их распределений является важным для анализа данных и прогнозирования результатов случайных событий. Это позволяет оценить вероятность наступления определенного события и принять обоснованные решения на основе полученных данных.

Закон больших чисел и центральная предельная теорема

Закон больших чисел утверждает, что среднее значение последовательности независимых и одинаково распределенных случайных величин сходится по вероятности к математическому ожиданию этой величины. Другими словами, при увеличении числа испытаний среднее значение будет все ближе к теоретическому среднему.

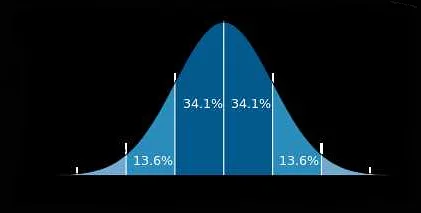
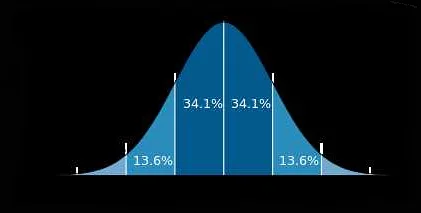
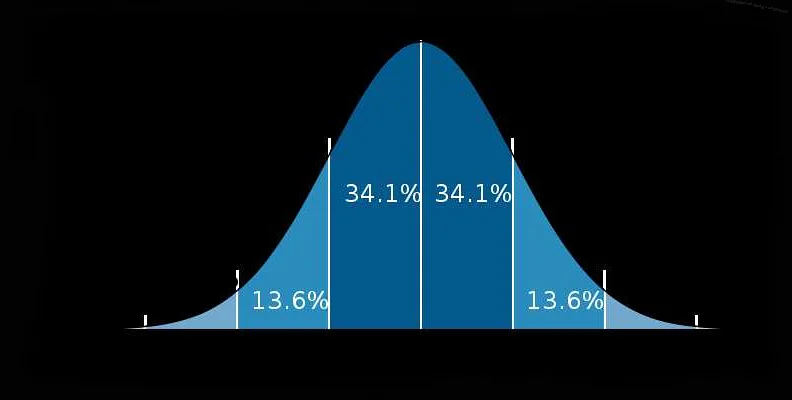
Центральная предельная теорема утверждает, что сумма или среднее большого числа независимых и одинаково распределенных случайных величин приближается к нормальному распределению. Это означает, что независимо от формы исходного распределения, если взять достаточно большую выборку, то ее сумма или среднее будут приближаться к нормальному распределению.

Закон больших чисел и центральная предельная теорема имеют важные практические применения. Например, они используются в статистике для вывода общих закономерностей, оценки вероятностей и построения доверительных интервалов. Также эти теоремы находят применение в экономике, физике, биологии и других областях, где требуется анализ случайных явлений и статистических данных.

Вопрос-ответ:

Какие основные принципы лежат в основе математического закона теории вероятности?

Математический закон теории вероятности основывается на двух основных принципах: принципе счета и принципе равной вероятности. Принцип счета утверждает, что если есть несколько возможных исходов, каждый из которых может произойти с n способами, то общее число исходов равно сумме этих способов. Принцип равной вероятности предполагает, что если все возможные исходы равновероятны, то вероятность каждого из них равна 1/n, где n — число всех возможных исходов.

Какие применения может иметь математический закон теории вероятности в реальной жизни?

Математический закон теории вероятности находит применение во многих областях реальной жизни. Например, он используется в статистике для анализа данных и прогнозирования, в финансовой математике для оценки рисков и доходности инвестиций, в медицине для оценки эффективности лечения и прогнозирования заболеваемости, в теории игр для определения оптимальных стратегий и т.д. Применение математического закона теории вероятности позволяет более точно оценивать вероятности различных событий и принимать обоснованные решения.

Как можно объяснить математический закон теории вероятности простыми словами?

Математический закон теории вероятности можно объяснить следующим образом: вероятность — это мера того, насколько вероятно возникновение какого-либо события. Закон теории вероятности утверждает, что вероятность события равна отношению числа благоприятных исходов к общему числу возможных исходов. Если у нас есть несколько исходов, каждый из которых может произойти с некоторой вероятностью, то сумма вероятностей всех исходов равна 1.

Какие еще принципы теории вероятности существуют?

Помимо основных принципов — принципа счета и принципа равной вероятности, существуют и другие принципы теории вероятности. Например, принцип условной вероятности, который говорит о том, что вероятность события A при условии, что произошло событие B, равна отношению вероятности одновременного происхождения событий A и B к вероятности события B. Также существует принцип независимости, который говорит о том, что вероятность совместного происхождения двух независимых событий равна произведению их вероятностей.

Зачем нужна теория вероятности?

Теория вероятности является фундаментальной математической теорией, которая позволяет оценивать вероятность наступления различных событий. Она широко применяется во многих областях, таких как статистика, физика, экономика, биология и другие. Теория вероятности позволяет принимать обоснованные решения на основе вероятностных данных и проводить статистические исследования.

Видео по теме: