Что изучает математическое моделирование

Математическое моделирование изучает процесс создания и анализа математических моделей, которые представляют реальные системы или явления. Эта наука позволяет предсказывать и оптимизировать поведение систем, а также исследовать их свойства и взаимодействия. Узнайте больше о том, как математическое моделирование помогает в решении сложных задач в различных областях науки и техники.

Математическое моделирование является важной областью науки, которая изучает создание и анализ математических моделей, используемых для описания и предсказания различных физических, биологических, социальных и экономических процессов. Оно позволяет упростить сложные реальные системы и представить их в виде математических уравнений и графов, что значительно облегчает исследование и анализ таких систем.

Одним из основных аспектов математического моделирования является выбор подходящей математической модели для конкретной системы. Это может быть система дифференциальных уравнений, модель случайного процесса, графовая модель и другие. Каждая модель имеет свои особенности и предназначена для описания определенного типа систем.

Применение математического моделирования находит широкое применение в различных областях науки и техники. Оно используется в физике, химии, биологии, экономике, социологии и других дисциплинах для изучения и предсказания поведения различных систем. Например, математическое моделирование позволяет предсказать изменение погоды, разработать новые лекарства, оптимизировать процессы производства, анализировать рынки и т.д.

Математическое моделирование является мощным инструментом, который помогает нам лучше понять и контролировать окружающий мир. Оно позволяет проводить эксперименты в виртуальной среде, что помогает сократить затраты на проведение реальных экспериментов и снизить риск возникновения нежелательных последствий.

В заключение, математическое моделирование играет важную роль в современной науке и технике. Оно помогает нам более глубоко понять и описать различные системы, предсказать их поведение и разработать оптимальные стратегии для достижения желаемых результатов. Благодаря математическому моделированию, мы можем решать сложные задачи и принимать обоснованные решения на основе точных расчетов и анализа данных.

Основные понятия и определения

Математическая модель — это формальное описание системы или процесса с помощью математических символов, уравнений и операций.

Переменная — это символ, представляющий неизвестное значение или характеристику системы или процесса, которое может меняться во времени или в зависимости от других переменных.

Параметр — это символ, представляющий известное или задаваемое значение или характеристику системы или процесса, которое не меняется во время моделирования.

Функция — это математическое правило или зависимость, которая связывает переменные и параметры в математической модели.

Уравнение — это математическое выражение, в котором две или более величины равны друг другу и связываются друг с другом через определенные операции.

Система уравнений — это набор двух или более уравнений, которые связывают несколько переменных и параметров, и используются для описания сложных взаимосвязей в математической модели.

Аналитическое решение — это процесс нахождения точного математического выражения для переменных или параметров в математической модели на основе решения системы уравнений.

Численное решение — это процесс приближенного нахождения значений переменных или параметров в математической модели с использованием численных методов и алгоритмов.

Симуляция — это процесс имитации поведения системы или процесса на компьютере с помощью математической модели и численного решения, что позволяет предсказывать и анализировать различные сценарии и результаты.

Валидация — это процесс проверки точности и достоверности математической модели на основе сравнения ее результатов с экспериментальными данными или другими известными моделями.

Применение математического моделирования — это использование математических моделей для решения конкретных задач и принятия решений в различных областях, таких как физика, экономика, биология, инженерия и др.

Видео по теме:

Математическое моделирование в науке

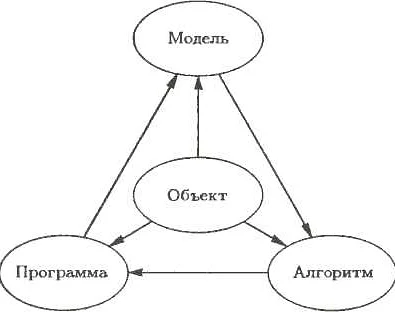
Математическое моделирование может быть использовано во многих областях науки, включая физику, химию, биологию, экологию, экономику и социологию. Например, в физике математические модели могут использоваться для описания движения тел, электромагнитных полей или квантовых систем. В биологии они могут использоваться для исследования популяционной динамики, эволюции или действия лекарственных препаратов на организм.

Важным аспектом математического моделирования является возможность проведения виртуальных экспериментов. Это позволяет ученым изучать системы, которые сложно или невозможно изучать в реальных условиях. Например, математическое моделирование может использоваться для исследования климатических изменений на планете, поведения финансовых рынков или распространения эпидемий.

Однако следует отметить, что математическое моделирование имеет свои ограничения. Модели могут быть упрощенными и не всегда точно описывать реальность. Кроме того, модели могут быть чувствительны к начальным условиям и параметрам, что может приводить к неточным результатам. Поэтому важно проводить верификацию и валидацию моделей, сравнивая их результаты с экспериментальными данными и проверяя их точность и применимость.

В заключение, математическое моделирование является важным инструментом в научных исследованиях. Оно позволяет ученым лучше понять и предсказать поведение сложных систем, а также проводить виртуальные эксперименты. Однако необходимо учитывать ограничения и проводить проверку моделей, чтобы обеспечить их точность и применимость.

Применение математического моделирования в физике

Математическое моделирование помогает физикам формализовать и упростить сложные физические системы, представив их в виде математических уравнений. Эти уравнения могут быть решены с использованием численных методов или аналитически, что позволяет получить предсказания о поведении системы в различных условиях.

Примеры применения математического моделирования в физике включают моделирование движения планет в солнечной системе, распространение света в оптических системах, взаимодействие частиц в элементарных частицах и многое другое. Математическое моделирование также широко используется для разработки новых физических теорий и проверки существующих гипотез.

Одним из основных преимуществ математического моделирования в физике является возможность проведения виртуальных экспериментов, которые могут быть трудно или невозможно выполнить в реальности. Это позволяет исследовать различные аспекты физических явлений, оптимизировать системы и предсказывать их поведение без необходимости проведения физических экспериментов.

Таким образом, математическое моделирование играет важную роль в физике, позволяя ученым более глубоко понять и объяснить различные физические явления, а также использовать этот знания для разработки новых технологий и решения практических задач. Оно является незаменимым инструментом для развития физики и расширения нашего понимания мира.

Вопрос-ответ:

Что такое математическое моделирование?

Математическое моделирование — это процесс создания математической модели, которая описывает поведение и свойства реального объекта или системы. Математическая модель представляет собой абстрактное представление объекта или системы, основанное на математических уравнениях и законах.

Какие основные аспекты изучает математическое моделирование?

Математическое моделирование изучает различные аспекты реальных объектов и систем, такие как их структура, свойства, динамика и взаимодействие. Оно позволяет исследовать процессы, которые невозможно или трудно изучать в реальном мире, и предсказывать их поведение в различных условиях.

Каким образом математическое моделирование применяется в науке и технике?

Математическое моделирование играет важную роль в науке и технике. Оно используется для исследования физических процессов, разработки новых технологий, оптимизации систем и прогнозирования результатов экспериментов. Например, в физике моделируются движение частиц, в экономике — рыночные процессы, в климатологии — изменение климата и т.д.

Каким образом математическое моделирование применяется в медицине?

Математическое моделирование находит применение в медицине для изучения биологических систем, прогнозирования эффективности лекарственных препаратов, оптимизации дозировки лекарств, моделирования распространения инфекционных заболеваний и т.д. Оно помогает улучшить процессы диагностики, лечения и прогнозирования результатов лечения пациентов.

Каким образом математическое моделирование применяется в экологии?

Математическое моделирование в экологии используется для изучения взаимодействия живых организмов и окружающей среды, прогнозирования изменения численности популяций, анализа воздействия антропогенных факторов на экосистемы и разработки мер по их улучшению. Также математическое моделирование позволяет оценивать экологические риски и разрабатывать стратегии устойчивого развития.

Роль математического моделирования в экономике

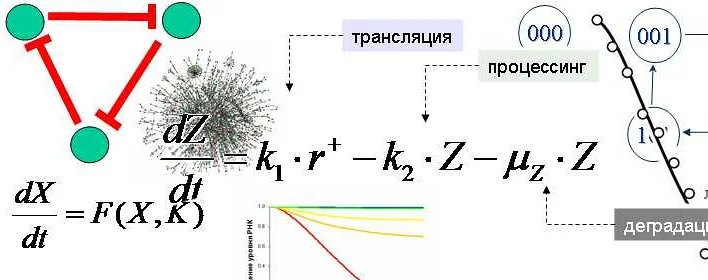
Математическое моделирование играет важную роль в экономике, помогая анализировать и прогнозировать сложные экономические явления. Оно позволяет установить взаимосвязь между различными переменными и предсказать их влияние на экономические процессы.

Одним из основных применений математического моделирования в экономике является оптимизация решений. С помощью математических моделей можно найти оптимальные решения для различных экономических задач, таких как оптимальное распределение ресурсов, оптимальное планирование производства или оптимальное управление финансовыми потоками.

Математическое моделирование также помогает в анализе рисков и прогнозировании экономических сценариев. С помощью моделей можно оценить вероятность возникновения различных событий и их влияние на экономическую систему. Это позволяет принимать более обоснованные решения и эффективно управлять рисками.

Кроме того, математическое моделирование позволяет проводить экономические эксперименты и исследования. С помощью моделей можно определить влияние различных факторов на экономические показатели и проанализировать их взаимодействие. Это позволяет лучше понять причинно-следственные связи в экономической системе и разработать эффективные стратегии развития.

Таким образом, математическое моделирование играет важную роль в экономике, помогая анализировать сложные экономические явления, принимать обоснованные решения и прогнозировать развитие экономической системы.

Использование математического моделирования в биологии

Одним из основных применений математического моделирования в биологии является моделирование популяций. Математические модели могут помочь определить факторы, влияющие на рост и развитие популяций, и предсказать, как они будут изменяться со временем. Например, можно построить модель для изучения влияния изменения климата на распределение и численность определенного вида животных.

Кроме того, математическое моделирование применяется для изучения динамики заболеваний и распространения эпидемий. Модели позволяют анализировать различные факторы, такие как скорость передачи инфекции, иммунитет и эффективность мер по контролю распространения болезни. Это позволяет спрогнозировать распространение заболевания и оценить эффективность различных стратегий борьбы с ним.

Также математическое моделирование используется для изучения генетических процессов. Модели могут помочь понять, как гены взаимодействуют друг с другом и с окружающей средой, и какие изменения в генетической информации могут привести к различным нарушениям и заболеваниям. Кроме того, моделирование может помочь в разработке новых методов лечения и генной терапии.

В целом, использование математического моделирования в биологии позволяет более глубоко понять сложные биологические процессы и предсказать их поведение в различных условиях. Это помогает развитию биологической науки и способствует разработке новых методов и стратегий в биологических исследованиях.

Математическое моделирование в социальных науках

Моделирование в социальных науках позволяет проводить эксперименты на компьютере, чтобы исследовать различные сценарии и предсказать возможные результаты. С помощью математических моделей ученые могут изучать, как изменения в одной сфере влияют на другие аспекты социальной системы.

Применение математического моделирования в социальных науках имеет широкий спектр применений. Например, моделирование может использоваться для изучения социальных сетей и анализа их влияния на распространение информации или вирусов. Моделирование также может помочь в понимании динамики популяций, экономических процессов, политических систем и других социальных явлений.

Одним из основных преимуществ математического моделирования в социальных науках является возможность предсказывать результаты и оценивать эффективность различных стратегий. Это позволяет принимать более обоснованные решения и разрабатывать оптимальные стратегии в различных социальных сферах.

Математическое моделирование в социальных науках требует разработки и адаптации специализированных математических методов и моделей, которые учитывают особенности социальных систем. Такие модели могут быть сложными и требовать больших вычислительных ресурсов, но они позволяют исследователям получить новые знания и понимание о социальных процессах, которые могут быть полезны в различных областях, включая социологию, политологию, экономику и маркетинг.

Преимущества математического моделирования в социальных науках:Применение математического моделирования в социальных науках:

• Возможность предсказывать результаты и оценивать эффективность стратегий	• Изучение социальных сетей и их влияния на распространение информации
• Понимание динамики популяций, экономических процессов и политических систем	• Анализ динамики популяций и взаимодействия различных социальных факторов
• Разработка оптимальных стратегий в различных социальных сферах	• Исследование влияния социальных факторов на различные аспекты социальных систем

Применение математического моделирования в инженерии

Одним из основных применений математического моделирования в инженерии является создание компьютерных моделей, которые позволяют инженерам изучать различные аспекты работы системы без необходимости строить физические прототипы. Это существенно сокращает время и затраты на разработку новых технологий и устройств.

Математическое моделирование также применяется для оптимизации процессов производства. С помощью моделей инженеры могут анализировать различные варианты размещения оборудования, планировать распределение ресурсов и оптимизировать производственные цепочки. Это позволяет снизить затраты, повысить эффективность и качество производства.

В инженерии математическое моделирование используется также для анализа надежности и безопасности систем. С помощью моделей инженеры могут оценить вероятность отказа компонентов, предсказать поведение системы в экстремальных условиях и определить оптимальные меры по обеспечению безопасности.

Математическое моделирование также применяется для создания и оптимизации алгоритмов управления в различных инженерных системах. Модели позволяют инженерам проводить испытания и анализировать работу алгоритмов на компьютере, что делает возможным их улучшение и оптимизацию до реализации в реальных системах.

Таким образом, математическое моделирование играет важную роль в инженерии, предоставляя инженерам инструменты для анализа, проектирования и оптимизации различных систем. Оно позволяет ускорить и удешевить процессы разработки, повысить качество и эффективность инженерных решений.

Будущие направления развития математического моделирования

В будущем математическое моделирование будет продолжать развиваться и применяться во множестве областей. Ниже приведены несколько основных направлений, которые могут стать основой для будущего развития данной области:

1. Развитие компьютерных технологий	С постоянным развитием компьютерных технологий будут появляться новые возможности для математического моделирования. Усовершенствование аппаратного и программного обеспечения позволит обрабатывать большие объемы данных и решать более сложные задачи.
2. Интеграция различных дисциплин	В будущем математическое моделирование будет все больше интегрироваться с другими науками, такими как физика, химия, биология, экономика и т.д. Это позволит создавать более реалистичные и точные модели, учитывающие более широкий спектр факторов и закономерностей.
3. Развитие теории стохастических процессов	Теория стохастических процессов играет важную роль в математическом моделировании случайных и неопределенных процессов. В будущем ожидается развитие этой теории и создание новых методов и подходов для моделирования случайных явлений.
4. Применение машинного обучения	Машинное обучение представляет собой методы и алгоритмы, которые позволяют компьютерным системам обучаться на основе опыта и данных. В будущем математическое моделирование будет все больше использовать методы машинного обучения для создания более точных и эффективных моделей.
5. Развитие теории оптимизации	Теория оптимизации является важной составляющей математического моделирования. В будущем ожидается развитие новых методов и алгоритмов оптимизации, которые позволят решать более сложные задачи и улучшать качество моделей.

В целом, будущее математического моделирования обещает быть увлекательным и перспективным. Развитие технологий, интеграция различных дисциплин, развитие новых теорий и применение современных методов анализа данных позволят создавать все более точные и эффективные модели, которые будут иметь широкое применение в различных областях науки и практики.