Математика на сколько больше на сколько меньше

Математика на сколько больше на сколько меньше: понятие неравенства, сравнение чисел, операции сравнения, неравенства и их свойства.

Математика — это наука, которая изучает количество, структуру, пространство и изменение. Она является одной из фундаментальных дисциплин и играет важную роль в нашей повседневной жизни. В рамках математики существует множество концепций и принципов, которые помогают нам понять и использовать числа, отношения и операции.

Один из основных принципов математики — это понятие «на сколько больше на сколько меньше». Этот принцип позволяет сравнивать два числа и определить, насколько одно число больше или меньше другого. Для этого используются операции сравнения, такие как больше (>) и меньше (

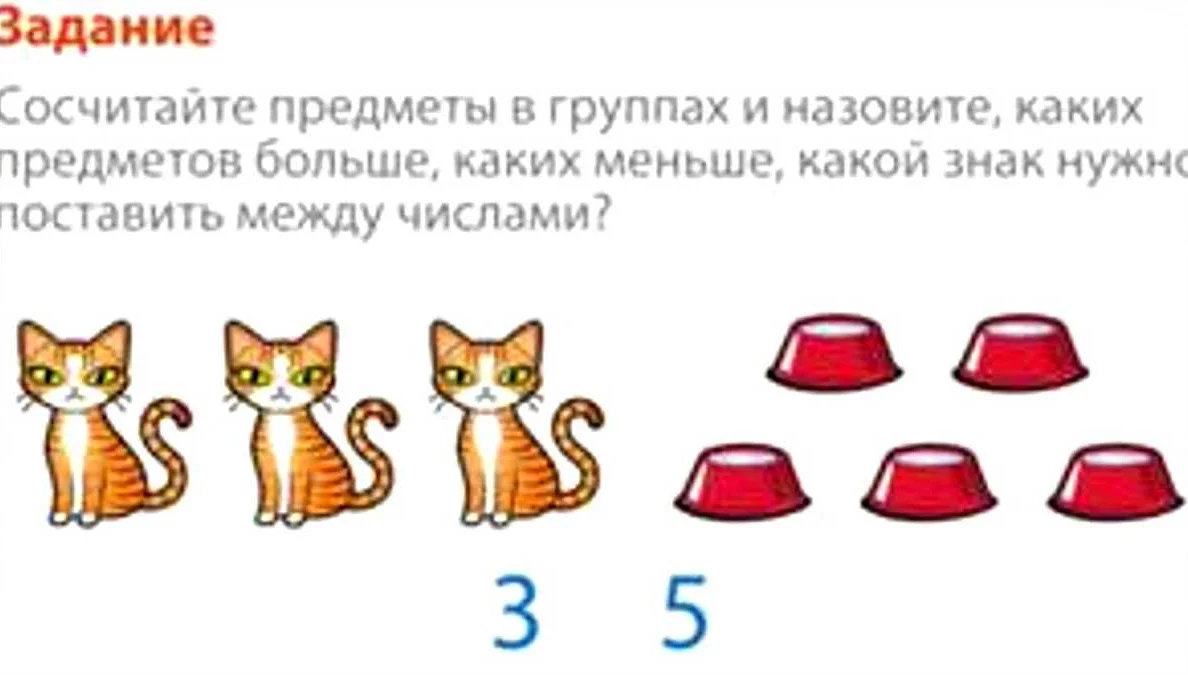
Например, если у нас есть два числа: 5 и 3, мы можем сказать, что число 5 больше числа 3 на 2. Или, с другой стороны, число 3 меньше числа 5 на 2.

Этот принцип применяется во многих областях нашей жизни. Например, при сравнении цен на товары, мы можем определить, насколько один товар дороже или дешевле другого. Также он используется в финансовых расчетах, анализе данных и многих других сферах.

Таким образом, понимание основных принципов математики, включая концепцию «на сколько больше на сколько меньше», помогает нам развивать логическое мышление, решать проблемы и делать осознанные выборы во многих ситуациях нашей повседневной жизни.

Математика: основные принципы и примеры

Основные принципы математики включают:

1. Аксиомы — это базовые и несомненные истины, на которых строится математическая система. Например, аксиома о равенстве утверждает, что если два объекта равны третьему, то они равны друг другу.
2. Определения — это формальные описания математических понятий. Определение числа Пи, например, устанавливает его значение как отношение длины окружности к ее диаметру.
3. Теоремы — это математические утверждения, которые доказаны на основе аксиом и определений. Теорема Пифагора, например, утверждает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.
4. Доказательства — это логические рассуждения и дедукции, которые подтверждают истинность теорем. Доказательство теоремы может быть представлено в форме логической цепи утверждений и выводов.

Примеры математических принципов и применений включают в себя:

• Арифметика — изучение свойств чисел и основных операций, таких как сложение, вычитание, умножение и деление.
• Геометрия — изучение свойств фигур и пространства, таких как треугольники, круги и параллелограммы.
• Алгебра — изучение алгебраических структур и операций, таких как уравнения, функции и многочлены.
• Вероятность и статистика — изучение случайных событий и анализ данных для принятия решений и выводов.

Математика играет важную роль в развитии логического мышления, а также в нашей повседневной жизни. Она помогает нам решать проблемы, анализировать информацию, прогнозировать результаты и понимать мир вокруг нас.

Основные понятия и определения

В математике сравнение двух чисел может быть выражено с помощью основных понятий «на сколько больше» и «на сколько меньше». Эти понятия помогают нам понять разницу между числами и оценить их отношение друг к другу.

На сколько больше: это выражение используется для сравнения двух чисел, где первое число больше второго. Например, если есть два числа: 7 и 3, то первое число (7) на сколько больше второго числа (3) можно рассчитать как 7 — 3 = 4. Таким образом, первое число на 4 больше второго.

На сколько меньше: это выражение используется для сравнения двух чисел, где первое число меньше второго. Например, если есть два числа: 5 и 8, то первое число (5) на сколько меньше второго числа (8) можно рассчитать как 8 — 5 = 3. Таким образом, первое число на 3 меньше второго.

Определения:

• Разность — это результат вычитания одного числа из другого. Разность между числами a и b обозначается как a — b.
• Положительная разность — это разность, которая получается, когда первое число больше второго.
• Отрицательная разность — это разность, которая получается, когда первое число меньше второго.

Например, разность между числами 8 и 3 будет положительной: 8 — 3 = 5. А разность между числами 3 и 8 будет отрицательной: 3 — 8 = -5.

Использование этих основных понятий и определений помогает нам лучше понять и анализировать числа, их отношения и различия.

Сложение и вычитание чисел

Сложение — это процесс объединения двух или более чисел в одно общее число, называемое суммой. Для сложения чисел мы используем знак «+». Например, 2 + 3 = 5. В этом примере мы складываем числа 2 и 3, и получаем сумму 5.

Вычитание — это процесс нахождения разности двух чисел. Для вычитания чисел мы используем знак «-«. Например, 7 — 4 = 3. В этом примере мы отнимаем от числа 7 число 4, и получаем разность 3.

При сложении и вычитании чисел мы также можем использовать отрицательные числа. Отрицательные числа указывают на отсутствие или отрицательное количество, и для их обозначения мы используем знак «-«. Например, -5 + 2 = -3. В этом примере мы складываем число -5 и число 2, и получаем сумму -3.

Сложение и вычитание также можно комбинировать в одной задаче. Например, 8 — 3 + 2 = 7. В этом примере мы сначала вычитаем число 3 из числа 8, а затем прибавляем число 2. Результатом будет число 7.

Знание основных принципов сложения и вычитания чисел очень важно для решения более сложных математических задач и применения их в повседневной жизни.

Умножение и деление чисел

Умножение двух чисел показывает, сколько раз одно число содержится в другом. Например, умножение числа 4 на число 3 дает результат 12, так как 4 содержится в 12 три раза.

Деление, наоборот, показывает, сколько раз число можно разделить на другое число. Например, деление числа 12 на число 4 дает результат 3, так как 12 можно разделить на 4 три раза без остатка.

Умножение и деление обладают свойствами коммутативности и ассоциативности:

Свойство коммутативности означает, что порядок умножаемых или делящихся чисел не влияет на результат операции. Например:

2 * 3 = 3 * 2

4 / 2 = 2 / 4

Свойство ассоциативности означает, что результат умножения или деления не зависит от порядка выполнения операций. Например:

(2 * 3) * 4 = 2 * (3 * 4)

(4 / 2) / 3 = 4 / (2 / 3)

Умножение и деление также могут быть использованы в комбинации с другими операциями, такими как сложение и вычитание, для выполнения более сложных вычислений.

Например, выражение 2 * (3 + 4) означает, что число 2 умножается на сумму чисел 3 и 4, что дает результат 14.

Важно помнить, что деление на ноль невозможно, так как не существует числа, которое можно разделить на ноль без остатка. Поэтому при делении числа на ноль возникает математическая ошибка.

Пропорции и проценты

Проценты — это способ выражения доли или части величины в процентном соотношении. Они позволяют измерять изменения или относительные значения величин.

Пропорции и проценты широко используются в различных областях, таких как финансы, статистика, экономика и торговля. Они помогают анализировать данные, делать прогнозы и принимать решения на основе полученных результатов.

Например, пропорции и проценты могут быть использованы для сравнения цен на товары, расчета скидок, определения роста популяции или вычисления доли дохода, потраченного на определенные категории расходов.

Важно уметь работать с пропорциями и процентами, чтобы правильно интерпретировать и анализировать информацию. Это поможет принимать обоснованные решения на основе данных и избегать ошибок в рассуждениях и заключениях.

Формулы и уравнения

Формулы и уравнения удобно использовать для решения различных задач и нахождения неизвестных значений. Часто в математике используются такие символы, как x, y и z, чтобы обозначать неизвестные значения.

Примеры формул:

• Площадь квадрата: S = a^2, где a — длина стороны квадрата.
• Площадь прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.
• Объем цилиндра: V = π * r^2 * h, где π — математическая константа «пи», r — радиус основания цилиндра, h — высота цилиндра.

Примеры уравнений:

• Уравнение прямой: y = kx + b, где k — коэффициент наклона прямой, b — свободный член.
• Квадратное уравнение: ax^2 + bx + c = 0, где a, b и c — коэффициенты, x — неизвестная.
• Уравнение окружности: (x — h)^2 + (y — k)^2 = r^2, где (h, k) — координаты центра окружности, r — радиус окружности.

Формулы и уравнения являются важным инструментом в математике и широко применяются в различных областях, таких как физика, экономика, статистика и другие.

Геометрия: площадь и периметр

Площадь — это мера площади поверхности фигуры. Она измеряется в квадратных единицах. Для различных фигур существуют различные способы вычисления площади. Например, для прямоугольника площадь равна произведению длины и ширины, для круга — квадрату радиуса, для треугольника — половине произведения основания и высоты.

Периметр — это сумма длин всех сторон фигуры. Он измеряется в линейных единицах. Для различных фигур существуют различные способы вычисления периметра. Например, для прямоугольника периметр равен удвоенной сумме длины и ширины, для круга — произведению диаметра на число Пи, для треугольника — сумме длин всех трех сторон.

Понимание площади и периметра фигур является важным в геометрии. Они позволяют определить размеры и свойства фигур, а также решать различные задачи, связанные с геометрией.

Важно помнить, что площадь и периметр могут быть использованы не только для простых фигур, но и для сложных многоугольников, кривых фигур и других геометрических объектов.

Таким образом, площадь и периметр являются основными понятиями геометрии, которые помогают изучать и понимать различные фигуры и их свойства.

Видео по теме:

Вопрос-ответ:

Какие принципы лежат в основе понятий «на сколько больше» и «на сколько меньше» в математике?

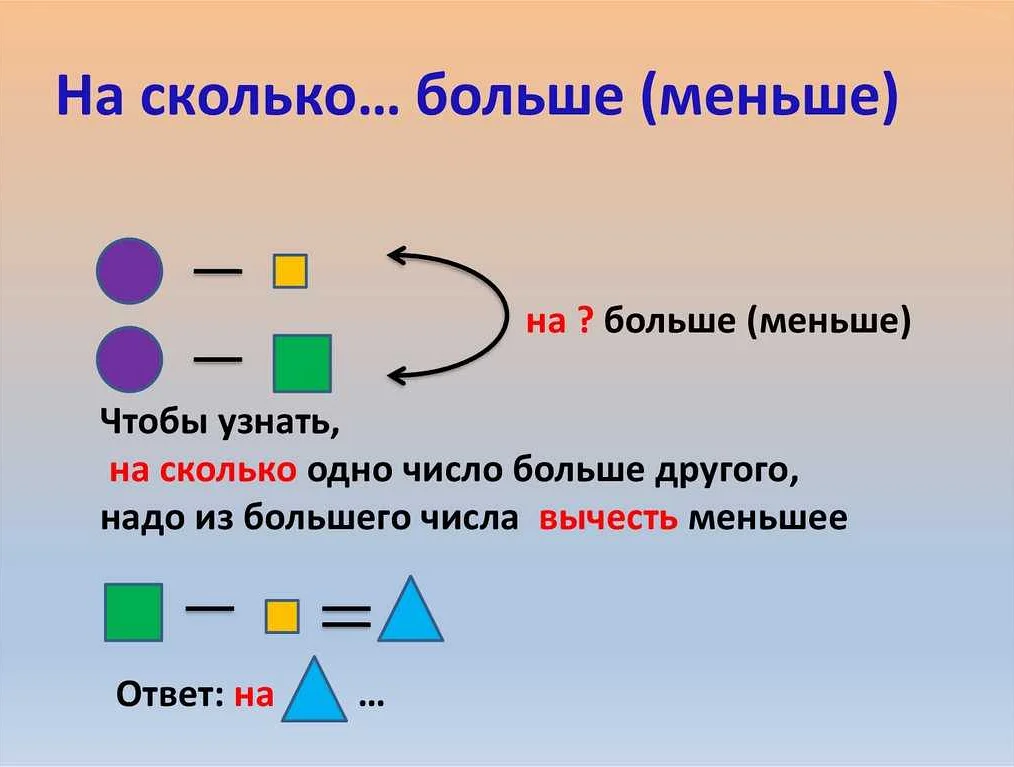
В математике понятия «на сколько больше» и «на сколько меньше» основаны на сравнении двух чисел. Чтобы определить, на сколько одно число больше или меньше другого, необходимо вычислить разность между этими числами.

Как вычислить разность между двумя числами?

Чтобы вычислить разность между двумя числами, необходимо вычесть из большего числа меньшее число. Например, чтобы найти разность между числами 7 и 3, нужно вычесть 3 из 7, что дает результат 4.

Можно ли определить, на сколько больше или меньше два числа, если они равны?

Если два числа равны, то разность между ними будет равна нулю. Это значит, что ни одно число не больше и не меньше другого.

Можно ли применять понятия «на сколько больше» и «на сколько меньше» к дробям?

Да, понятия «на сколько больше» и «на сколько меньше» могут применяться к дробям. Например, чтобы определить, на сколько одна дробь больше другой, нужно вычислить разность между ними, а затем сократить полученную дробь до несократимого вида.

Можно ли применять понятия «на сколько больше» и «на сколько меньше» к отрицательным числам?

Да, понятия «на сколько больше» и «на сколько меньше» также применимы к отрицательным числам. Если одно отрицательное число больше другого, то разность между ними тоже будет отрицательным числом.

Какие основные принципы математики связаны с понятием «на сколько больше на сколько меньше»?

Основные принципы математики, связанные с понятием «на сколько больше на сколько меньше», включают в себя идею сравнения двух чисел и определение их разности. Если одно число больше другого, то разница между ними положительна, а если одно число меньше другого, то разница будет отрицательна.

Как можно использовать понятие «на сколько больше на сколько меньше» в повседневной жизни?

Понятие «на сколько больше на сколько меньше» можно использовать в повседневной жизни для сравнения различных величин или количеств. Например, можно сравнить стоимость двух товаров и определить, на сколько один товар дороже или дешевле другого. Также это понятие может быть полезно при планировании расходов или определении разницы между двумя временными отрезками.

Тригонометрия: синус, косинус, тангенс

Синус угла в треугольнике равен отношению противоположной стороны к гипотенузе. Обозначается символом sin. Для вычисления значения синуса угла необходимо знать длину противоположной стороны и гипотенузы треугольника.

Косинус угла в треугольнике равен отношению прилежащей стороны к гипотенузе. Обозначается символом cos. Для вычисления значения косинуса угла необходимо знать длину прилежащей стороны и гипотенузы треугольника.

Тангенс угла в треугольнике равен отношению противоположной стороны к прилежащей стороне. Обозначается символом tan. Для вычисления значения тангенса угла необходимо знать длины противоположной и прилежащей сторон треугольника.

Знание синуса, косинуса и тангенса позволяет решать различные задачи в геометрии и физике, связанные с треугольниками и углами. Тригонометрия также находит применение в технических и научных расчетах.

Примеры использования:

1. Нахождение стороны треугольника, если известны два угла и длина одной стороны. При помощи синуса и косинуса можно выразить противоположную и прилежащую стороны, а затем найти третью сторону треугольника.

2. Решение задачи о движении объекта под углом к горизонту. Используя тангенс, можно выразить вертикальную и горизонтальную составляющие скорости и определить дальность полета объекта.

Тригонометрия является важной и неотъемлемой частью математики, позволяющей решать задачи, связанные с углами и сторонами треугольника.

Статистика и вероятность

Вероятность — это область математики, изучающая случайные и непредсказуемые события. Она помогает нам оценить вероятность наступления определенного события и прогнозировать его результаты. Вероятность может быть представлена числом от 0 до 1, где 0 означает невозможность наступления события, а 1 — его полную уверенность.

Примеры использования статистики и вероятности:

1. Статистика может использоваться для анализа результатов опросов и исследований. На основе статистических данных можно выявить тенденции и закономерности в мнении и поведении людей.

2. Вероятность может быть использована при принятии решений в условиях неопределенности. Например, при планировании проекта можно оценить вероятность его успешного завершения и принять решение о его реализации.

3. Комбинирование статистики и вероятности может помочь в прогнозировании будущих событий. Например, на основе статистических данных о прошлых продажах можно оценить вероятность успеха нового продукта на рынке.

В целом, знание статистики и вероятности позволяет нам лучше понимать и анализировать мир вокруг нас. Они играют важную роль в принятии решений и развитии научных исследований.