Когда математика делится на алгебру и геометрию
Содержимое
- 1 Когда математика делится на алгебру и геометрию
Алгебра и геометрия являются основными разделами математики. Узнайте, как они связаны и как они различаются, и почему они играют важную роль в нашей жизни.
Математика — это одна из самых старых наук, которая изучает структуру, свойства и отношения между числами, формами и объектами. Она имеет разные разделы, включая алгебру и геометрию, которые являются основными направлениями математического исследования.
Алгебра — это раздел математики, который изучает способы манипулирования символами и выражениями. Она включает в себя понятия переменных, уравнений, функций, алгоритмов и многих других. Алгебра позволяет решать различные математические задачи с помощью символьных операций и систематических методов.
Геометрия — это раздел математики, который изучает формы, размеры, отношения и свойства пространственных объектов, таких как точки, линии, плоскости и тела. Она использует абстрактные понятия и логические рассуждения для анализа и описания геометрических фигур и их взаимосвязей.
Алгебра и геометрия тесно связаны друг с другом и являются важными инструментами математического анализа и решения задач. Вместе они обеспечивают широкий спектр методов и подходов для изучения и понимания различных аспектов математики и ее применения в реальном мире.
Понимание разницы между алгеброй и геометрией позволяет математикам использовать соответствующие инструменты и методы для изучения и решения конкретных задач. Это также способствует развитию аналитического мышления, логического мышления и способности абстрагироваться от конкретных ситуаций в математическом моделировании и анализе данных.
Определение математики
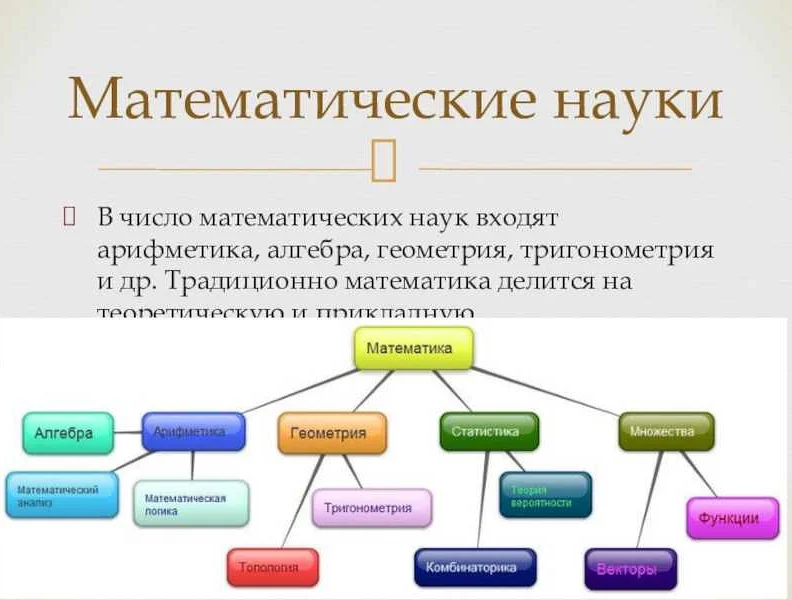
Математика имеет две основные разделы: алгебру и геометрию. Алгебра занимается числами, операциями над ними, а также изучением абстрактных объектов, таких как группы, кольца и поля. Геометрия, с другой стороны, изучает формы, пространство и отношения между ними.
Одной из важных особенностей математики является ее строгость и точность. Математическая логика и аксиоматический метод играют важную роль в построении математических теорий и доказательств.
Математика имеет широкий спектр приложений в различных областях, таких как физика, экономика, компьютерные науки и технические науки. Она также является важным инструментом для развития логического мышления и способности анализировать и решать проблемы.
В общем, математика является неотъемлемой частью нашей жизни и играет важную роль в понимании и описании мира вокруг нас.
Алгебра

Основные понятия алгебры включают в себя операции сложения, вычитания, умножения и деления, а также понятия равенства, неравенства и переменных. Изучение алгебры помогает развить логическое мышление, абстрактное мышление и решение сложных математических задач.
В алгебре также изучаются алгебраические уравнения и системы уравнений, которые позволяют находить значения неизвестных переменных. Алгебраические методы широко применяются в физике, экономике, компьютерных науках и других областях науки и техники.
Основные темы алгебрыПримеры
| Алгебраические операции | Сложение, вычитание, умножение, деление |
| Алгебраические уравнения | x + 2 = 5 |
| Системы уравнений | x + y = 3 2x — y = 1 |
| Поля и кольца | Множество действительных чисел |
| Группы | Множество симметрий квадрата |
Алгебра является одной из основных дисциплин школьного курса математики и основой для изучения других разделов математики, таких как аналитическая геометрия и математический анализ.
Основные понятия алгебры

Переменные – символы, используемые для обозначения неизвестных или изменяемых величин.
Выражения – математические комбинации чисел, переменных и операций, таких как сложение, вычитание, умножение и деление.
Уравнения – математические выражения, содержащие знак равенства и неизвестные величины, которые требуется найти.
Функции – отображения, которые связывают значения одной переменной с другими переменными.
Матрицы – таблицы чисел, упорядоченных в строках и столбцах.
Полиномы – математические выражения, состоящие из одного или нескольких слагаемых, в которых переменные возводятся в натуральные степени и перемножаются на числа.
Рациональные числа – числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами.
Комплексные числа – числа, которые можно представить в виде суммы действительной и мнимой части, где мнимая единица обозначается символом i.
Изучение этих основных понятий алгебры позволяет решать уравнения, находить значения переменных и проводить различные операции над числами и выражениями.
Геометрия

Основные объекты геометрии — это точки, прямые, плоскости, углы, фигуры и тела. Геометрия также описывает различные отношения между этими объектами, такие как параллельность, перпендикулярность, сходство и равенство.
Геометрия широко применяется в различных областях науки и техники. Например, в архитектуре и строительстве используются геометрические принципы при проектировании зданий и сооружений. В физике и инженерии геометрия используется для моделирования и анализа физических объектов и систем.
Одним из фундаментальных понятий геометрии является понятие пространства. Пространство — это абстрактная сущность, которая позволяет определить расстояния и отношения между объектами. В зависимости от количества измерений, пространство может быть одномерным (линия), двумерным (плоскость) или трехмерным (пространство).
Геометрия имеет свои основные ветви, такие как планиметрия и стереометрия. Планиметрия изучает геометрические фигуры и преобразования в двумерном пространстве, в то время как стереометрия занимается изучением трехмерных объектов и пространственных отношений.
В геометрии используется множество различных методов и инструментов, таких как построения с помощью циркуля и линейки, аналитическая геометрия, геометрические формулы и теоремы. Знание геометрии позволяет развивать способность анализировать и решать геометрические задачи, а также применять геометрические принципы в реальной жизни.
Ветви геометрииОписание
| Планиметрия | Изучение геометрических фигур и преобразований в двумерном пространстве |
| Стереометрия | Изучение трехмерных объектов и пространственных отношений |
| Топология | Изучение свойств и преобразований, сохраняющих геометрическую форму |
| Проективная геометрия | Изучение отношений между фигурами, не зависящих от размеров и формы |
Основные понятия геометрии
Точка – это основное понятие геометрии, которое не имеет размеров и обозначается заглавной буквой. Точка не имеет ни длины, ни ширины, ни высоты. Она является началом для определения других понятий.
Линия – это набор бесконечного числа точек, расположенных вдоль одной оси. Линию можно представить как бесконечно длинную и тонкую нить. Линия не имеет толщины и ширины.
Плоскость – это пространство, состоящее из бесконечного числа точек, расположенных в одной плоскости. Плоскость можно представить как бесконечно большую и тонкую поверхность. Плоскость не имеет толщины.
Угол – это область пространства между двумя лучами, имеющими общее начало. Угол измеряется в градусах и обозначается символом °. Угол можно классифицировать как острый (меньше 90°), прямой (равный 90°), тупой (больше 90°) или полный (равный 180°).
Отрезок – это часть прямой линии, ограниченная двумя точками. Отрезок имеет конечную длину и обозначается двумя точками, между которыми он находится.
Эти основные понятия геометрии являются фундаментальными для изучения более сложных тем и построения различных геометрических фигур.
Сходства и различия
Алгебра занимается изучением чисел и операций над ними. В алгебре используются символы и формулы для представления математических объектов и отношений. Она изучает алгебраические структуры, такие как множества, группы, кольца и поля, и решение уравнений.
Геометрия, с другой стороны, изучает фигуры и их свойства. Она использует пространственное представление и графические модели для изучения различных геометрических объектов, таких как точки, линии, плоскости и тела. Геометрия также изучает преобразования, симметрию и измерения.
Одно из главных сходств между алгеброй и геометрией заключается в их общей цели – анализе и изучении математических объектов и их взаимосвязей. Обе дисциплины используют логическое мышление и формальные методы для решения задач, а также имеют свои собственные термины и обозначения.
Однако у алгебры и геометрии также есть свои специфические черты и методы. Алгебра более абстрактна, она работает с символами и формулами, а геометрия более конкретна, используя графическое представление объектов. Алгебраические методы широко применяются в анализе данных и в различных научных и инженерных областях, в то время как геометрические методы часто используются в физике, архитектуре и компьютерной графике.
Таким образом, алгебра и геометрия обеспечивают различные подходы к изучению математических объектов и являются важными дисциплинами в математике, которые часто дополняют друг друга и применяются в различных областях знания и практической деятельности.
Алгебра и геометрия: общие черты
Одной из главных общих черт алгебры и геометрии является то, что они оба изучают свойства и отношения между математическими объектами. Однако, предметы исследования в алгебре и геометрии различаются.
В алгебре основными объектами являются числа, переменные и операции над ними, такие как сложение, вычитание, умножение и деление. Алгебра изучает различные алгебраические структуры, такие как группы, кольца и поля, и исследует их свойства и взаимоотношения.
В геометрии основными объектами являются фигуры, пространства и отношения между ними. Геометрия изучает размеры, формы, расположение и свойства геометрических объектов, таких как точки, линии, плоскости, многоугольники и тела.
Однако, алгебра и геометрия также взаимосвязаны и взаимообогащают друг друга. Например, алгебра может использоваться для решения геометрических задач, а геометрия может предоставлять интуитивные представления для алгебраических концепций.
Изучение алгебры и геометрии позволяет развить аналитическое и геометрическое мышление, логическое мышление и умение решать разнообразные задачи. Поэтому оба эти раздела математики являются важными компонентами образования и науки.
Применение в реальной жизни

Математика, включая алгебру и геометрию, имеет широкое применение в реальной жизни. Она играет важную роль во многих сферах нашей жизни, включая науку, технологию, экономику и даже повседневные задачи.
В науке математика используется для моделирования и предсказания физических явлений. Формулы и уравнения позволяют ученым описывать и объяснять различные процессы и явления, от движения тел до электромагнитных волн. Алгебра и геометрия помогают структурировать и анализировать данные, полученные в ходе экспериментов и наблюдений.
В технологии математика применяется для разработки и анализа алгоритмов, программ и компьютерных моделей. Алгебра используется для работы с переменными и вычислениями, а геометрия помогает визуализировать и анализировать пространственные данные. Математические методы также используются в области искусственного интеллекта, машинного обучения и криптографии.
В экономике и финансах математика применяется для моделирования и анализа финансовых рынков, прогнозирования цен на акции и другие финансовые инструменты. Алгебра и геометрия помогают в решении задач оптимизации, планирования производства и распределения ресурсов.
Наконец, математика применяется и в повседневной жизни. Она помогает в решении задач бюджетирования и управления личными финансами, в расчете площади и объема при ремонте или строительстве, а также в анализе данных и принятии решений на основе статистики.
Таким образом, математика, включая алгебру и геометрию, является неотъемлемой частью нашей жизни. Ее применение в науке, технологии, экономике и повседневных задачах помогает нам лучше понимать и управлять миром вокруг нас.
Алгебра и геометрия в науке и технике
Алгебра является одним из основных инструментов в научных исследованиях и инженерной деятельности. Она позволяет изучать и описывать математические структуры и их взаимосвязи. Алгебраические методы используются в различных областях, таких как физика, информатика, экономика и многие другие.
Геометрия, в свою очередь, изучает формы, пространственные отношения и их свойства. Она позволяет строить модели объектов и анализировать их геометрические характеристики. Геометрические методы применяются в архитектуре, машиностроении, компьютерной графике и во многих других областях науки и техники.
Эти два раздела математики тесно взаимосвязаны и дополняют друг друга. Алгебраические методы позволяют формализовать и анализировать геометрические объекты, а геометрические методы позволяют визуализировать и геометризировать алгебраические структуры.
Использование алгебры и геометрии в науке и технике позволяет ученому или инженеру решать сложные задачи, прогнозировать результаты и создавать новые технологии. Они являются неотъемлемой частью современного мира и играют важную роль в развитии науки и техники.
Вопрос-ответ:
Что такое алгебра и геометрия?
Алгебра и геометрия — это два раздела математики, которые изучают разные аспекты чисел и фигур. Алгебра занимается операциями, связанными с числами и их свойствами, а геометрия изучает пространственные формы и отношения между ними.
Какие основные понятия изучаются в алгебре?
В алгебре изучаются такие понятия, как переменные, уравнения, функции, многочлены, матрицы и многое другое. Это позволяет решать различные задачи, связанные с арифметическими операциями, анализом данных и моделированием.
Какие основные понятия изучаются в геометрии?
В геометрии изучаются такие понятия, как точки, линии, фигуры, углы, расстояния и многое другое. Это позволяет анализировать и описывать пространственные формы, находить их свойства и решать задачи, связанные с конструкциями и измерениями.
Как алгебра и геометрия взаимосвязаны?
Алгебра и геометрия взаимосвязаны и взаимодополняют друг друга. Например, графическое представление алгебраических уравнений позволяет лучше понять их геометрический смысл. И наоборот, геометрические построения могут быть основаны на алгебраических методах. Оба раздела математики важны и применяются в различных областях науки и техники.
Зачем нужно изучать алгебру и геометрию?
Изучение алгебры и геометрии развивает логическое мышление, абстрактное мышление и способность анализировать информацию. Они помогают понимать и решать сложные задачи, а также находить рациональные решения. Знания в алгебре и геометрии также являются основой для изучения более сложных математических теорий и прикладных наук.
Роль в образовании

Основная цель изучения математики — развитие логического мышления, аналитических навыков и способности решать сложные проблемы. В процессе изучения математики учащиеся учатся анализировать, рассуждать, прогнозировать и применять полученные знания в различных ситуациях.
Математика также помогает развивать навыки решения задач, что является важным навыком для жизни в современном мире. Знание математики позволяет людям понимать и использовать информацию в науке, экономике, финансах, технологиях и других областях.
Геометрия, в свою очередь, помогает учащимся развивать пространственное мышление и представление о формах и структурах. Она также имеет практическое применение в архитектуре, инженерии, дизайне и других областях.
В целом, изучение математики, включая алгебру и геометрию, важно для образования, так как оно помогает развивать критическое мышление, аналитические навыки и способность решать сложные задачи. Оно также имеет практическое применение в различных профессиональных областях и помогает людям лучше понимать и использовать информацию в различных сферах жизни.
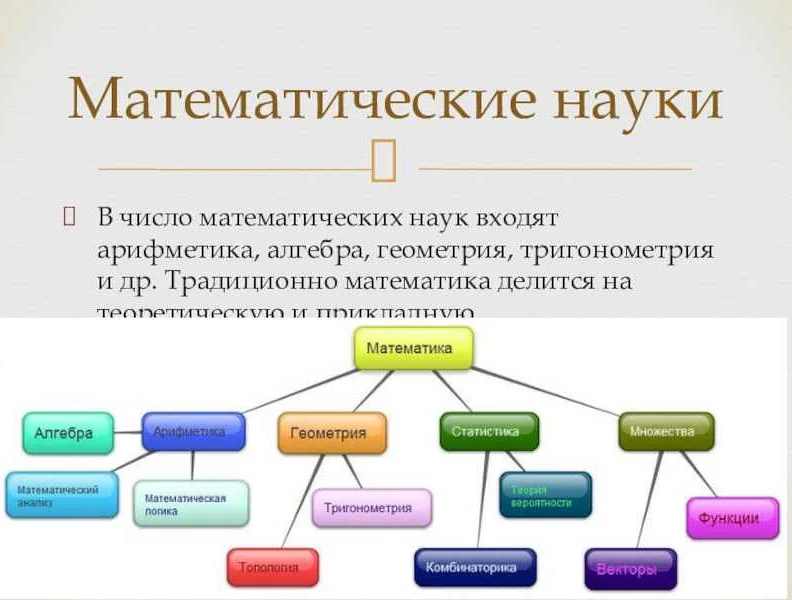



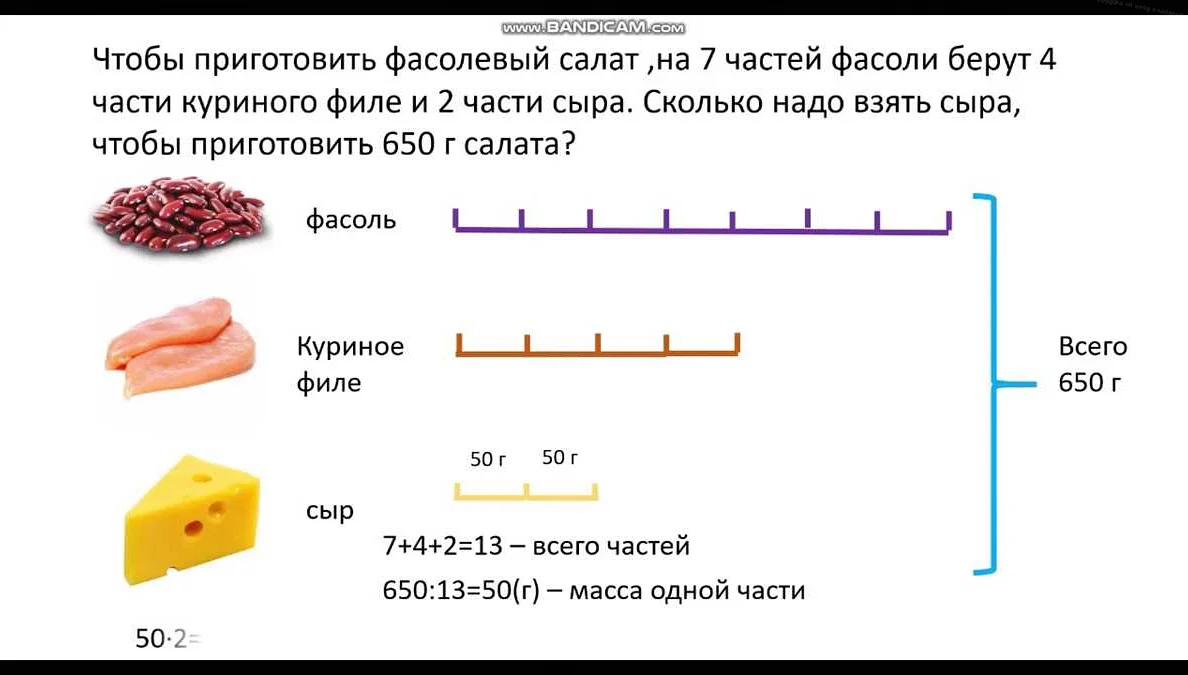
Статья очень интересная и понятная. Математика всегда была для меня непростым предметом, но после прочтения этой статьи я лучше понимаю разделение на алгебру и геометрию. Оказывается, алгебра и геометрия — это две взаимосвязанные ветви математики, каждая из которых имеет свои особенности и применения. Алгебра больше связана с абстрактными числами, формулами и уравнениями, в то время как геометрия изучает пространственные фигуры и их свойства. Я поняла, что обе эти ветви являются важными и необходимыми для полноценного понимания математики. Теперь я готова глубже изучать их и улучшать свои знания в этой области. Большое спасибо за статью!
Математика — это наука, которая делится на несколько разделов, алгебру и геометрию. Алгебра изучает уравнения, формулы, числа и операции над ними, тогда как геометрия занимается изучением фигур, пространственных отношений и свойств объектов. Оба раздела математики имеют свои особенности и предназначены для решения различных задач. Алгебра — это логический раздел математики, который помогает решать уравнения и выражения. Она является основой для понимания более сложных математических концепций и является неотъемлемой частью вычислительной науки и физики. Алгебра также развивает логическое мышление и аналитические навыки, что полезно не только в математике, но и в других областях жизни. Геометрия, с другой стороны, изучает формы, размеры и свойства геометрических объектов, таких как линии, углы, плоскости и объемы. Она имеет практическое применение в архитектуре, инженерии и дизайне. Геометрия помогает нам понять и визуализировать мир вокруг нас, а также развивает наше пространственное мышление. Оба раздела математики важны и взаимосвязаны. Знание как алгебры, так и геометрии позволяет лучше понимать мир и решать различные задачи. Они помогают развить наше мышление, логику и аналитические навыки, которые могут быть полезны во многих аспектах нашей жизни. Поэтому важно изучать оба раздела математики и использовать их вместе для достижения лучших результатов.