Что такое множество натуральных чисел в математике

Множество натуральных чисел в математике — это набор положительных целых чисел, начинающийся с единицы и продолжающийся бесконечно. Узнайте, как определить и использовать множество натуральных чисел в различных математических операциях.

Математика — это наука, которая изучает различные аспекты чисел, их свойства и взаимосвязи. Одним из важных понятий в математике является множество натуральных чисел. Натуральные числа — это положительные целые числа, начиная с единицы и продолжая бесконечно вверх.

Множество натуральных чисел обозначается символом N, и оно является одним из основных множеств в математике. Оно включает в себя числа 1, 2, 3, 4 и так далее. Множество натуральных чисел имеет несколько особых свойств, которые играют важную роль в различных математических операциях и доказательствах.

Важным свойством множества натуральных чисел является то, что оно является бесконечным. То есть, независимо от того, сколько чисел уже присутствует в множестве, всегда можно добавить следующее число. Это свойство позволяет использовать множество натуральных чисел для описания процессов, которые продолжаются во времени, таких как перечисление элементов или увеличение количества.

Кроме того, множество натуральных чисел является упорядоченным. Каждое число в множестве имеет определенное положение, которое зависит от его величины. Большие числа находятся дальше от начала множества, а меньшие числа находятся ближе к началу. Это позволяет проводить сравнения и установить отношения между числами в множестве натуральных чисел.

Множество натуральных чисел является одним из фундаментальных понятий в математике и является основой для построения других множеств и числовых систем. Оно играет важную роль в арифметике, алгебре, геометрии и других разделах математики. Понимание свойств и характеристик множества натуральных чисел позволяет решать различные задачи и проводить доказательства в математическом анализе.

Что такое множество натуральных чисел?

Множество натуральных чисел, обозначаемое символом ℕ, это особый тип множества в математике, который включает все положительные целые числа, начиная с единицы (1) и продолжая бесконечно: 1, 2, 3, 4, 5 и так далее. Другими словами, множество натуральных чисел состоит из всех чисел, которые можно получить путем последовательного прибавления единицы к предыдущему числу.

Множество натуральных чисел широко используется в математике и других науках, таких как физика и информатика, благодаря своей простоте и удобству для счета и упорядочения объектов. Например, оно используется для подсчета количества объектов в некоторой коллекции или для обозначения порядка событий во времени.

Множество натуральных чисел имеет несколько важных свойств. Во-первых, оно является бесконечным, то есть не имеет конечного или максимального элемента. Во-вторых, оно упорядочено по возрастанию, что означает, что каждое следующее число больше предыдущего. Наконец, оно обладает свойством плотности, что означает, что между любыми двумя числами из множества всегда можно найти еще одно число.

Видео по теме:

Определение множества натуральных чисел

Множество натуральных чисел, обозначаемое символом ℕ, состоит из всех положительных целых чисел, начиная с единицы и без десятичных или дробных частей. Множество натуральных чисел можно записать следующим образом:

ОбозначениеОписание

ℕ	Множество натуральных чисел
{1, 2, 3, 4, 5, …}	Перечисление натуральных чисел

Множество натуральных чисел содержит бесконечное количество элементов и является частью более общего множества целых чисел. Оно используется для описания количества объектов или позиции в нумерации.

Свойства множества натуральных чисел:

1. Множество натуральных чисел является бесконечным.
2. Множество натуральных чисел не содержит нуля и отрицательных чисел.
3. Множество натуральных чисел упорядочено по возрастанию.
4. Множество натуральных чисел можно оперировать арифметическими операциями, такими как сложение, вычитание, умножение и деление.

Множество натуральных чисел играет важную роль в различных областях математики и науки, и является основой для построения других множеств, таких как множество целых, рациональных и вещественных чисел.

Состав множества натуральных чисел

Множество натуральных чисел обозначается символом N и включает в себя все положительные целые числа, начиная с 1. То есть, множество натуральных чисел можно записать следующим образом: N = {1, 2, 3, 4, 5, …}.

Основные свойства множества натуральных чисел:

• Бесконечность: Множество натуральных чисел не имеет верхней границы и состоит из бесконечного количества элементов.
• Упорядоченность: Элементы множества натуральных чисел расположены в порядке возрастания, начиная с 1.
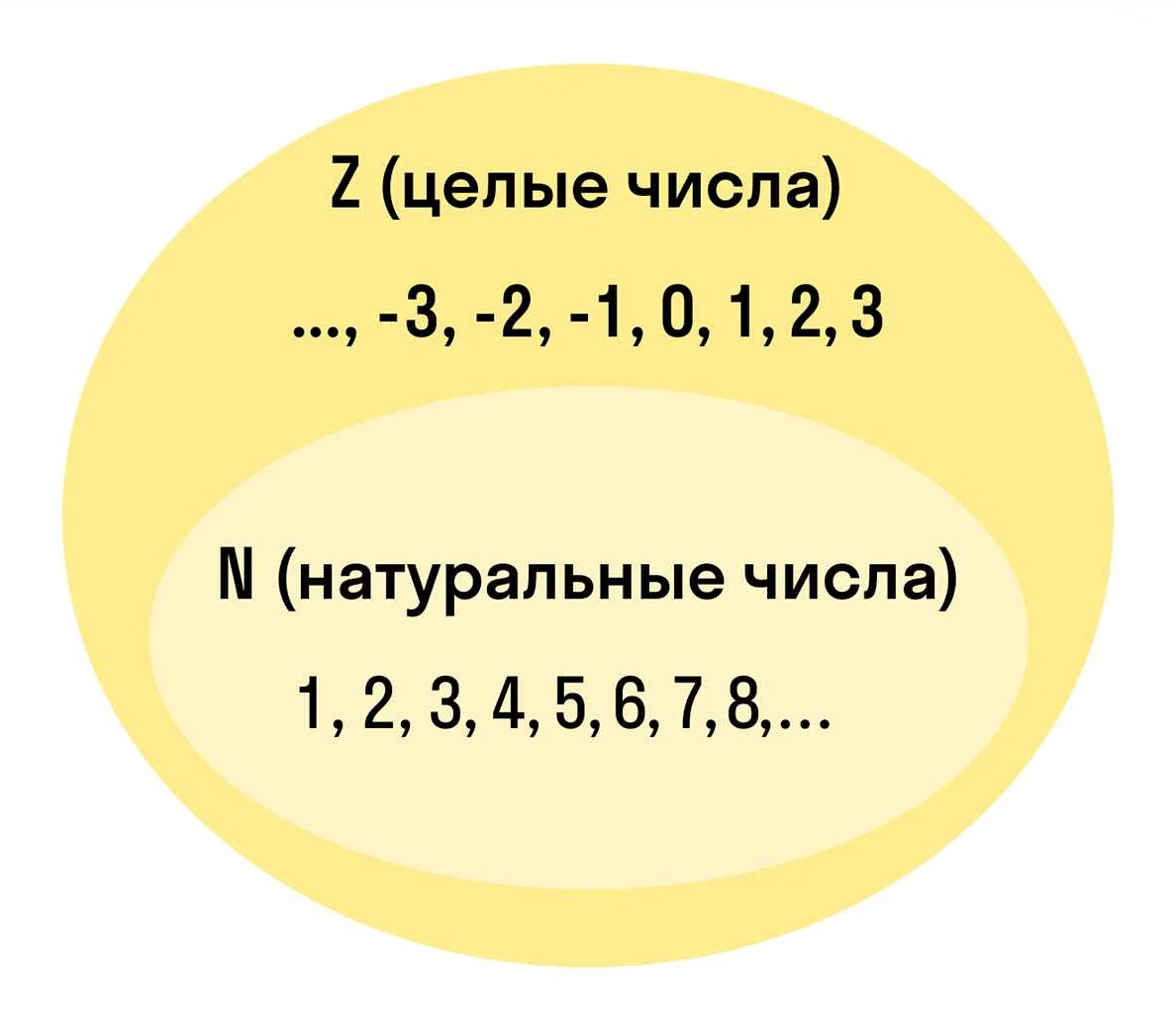
• Подмножество множества целых чисел: Множество натуральных чисел является подмножеством множества целых чисел Z, то есть каждое натуральное число также является целым числом.

Множество натуральных чисел широко используется в математике и других научных дисциплинах для описания исчисления, счета, и множества объектов, таких как люди, предметы или явления.

Свойства множества натуральных чисел

1. Бесконечность. Множество натуральных чисел бесконечно. Это означает, что для любого натурального числа n существует следующее натуральное число, большее n.

2. Упорядоченность. Множество натуральных чисел упорядочено по возрастанию. Каждое следующее число больше предыдущего.

3. Замкнутость относительно сложения. Если a и b — натуральные числа, то их сумма a + b также является натуральным числом.

4. Замкнутость относительно умножения. Если a и b — натуральные числа, то их произведение a * b также является натуральным числом.

5. Единственность нуля. Натуральные числа не содержат нуля. Ноль является единственным натуральным числом, не принадлежащим множеству натуральных чисел.

6. Отсутствие отрицательных чисел. Множество натуральных чисел не содержит отрицательных чисел. Все числа в этом множестве положительные.

7. Принадлежность к числам. Множество натуральных чисел является подмножеством целых чисел, рациональных чисел, вещественных чисел и комплексных чисел.

8. Натуральное число 1. Натуральное число 1 является наименьшим натуральным числом и не имеет предшественника.

Мощность множества натуральных чисел

Множество натуральных чисел является бесконечным и содержит все положительные целые числа, начиная с единицы. Мощность множества натуральных чисел несчётно-бесконечная, что означает, что невозможно установить взаимно-однозначное соответствие между натуральными числами и натуральными числами.

Мощность множества натуральных чисел можно сравнить с мощностью других бесконечных множеств. Например, мощность множества рациональных чисел (всех чисел, которые можно представить в виде дроби) также является несчётно-бесконечной. Однако, мощность множества действительных чисел (всех чисел на числовой прямой) считается континуально-бесконечной, то есть большей, чем мощность множества натуральных чисел.

Мощность множества натуральных чисел имеет важное значение в различных областях математики, включая теорию алгоритмов, теорию вероятности и математическую логику.

МножествоМощность

Натуральные числа	Неcчётно-бесконечная
Рациональные числа	Неcчётно-бесконечная
Действительные числа	Континуально-бесконечная

Операции над множеством натуральных чисел

Множество натуральных чисел обладает рядом особенностей, которые позволяют выполнять над ними различные операции.

Сложение: Операция сложения позволяет нам объединять два или более натуральных числа и получать в результате новое число, называемое суммой. Например, если мы сложим числа 3 и 5, то получим сумму равную 8.

Пример: 3 + 5 = 8

Вычитание: Операция вычитания позволяет нам находить разность между двумя натуральными числами. Результат вычитания называется разностью. Например, если мы вычтем из числа 8 число 3, то получим разность равную 5.

Пример: 8 — 3 = 5

Умножение: Операция умножения позволяет нам получать произведение двух или более натуральных чисел. Произведение является результатом умножения. Например, если мы умножим числа 2 и 4, то получим произведение равное 8.

Пример: 2 * 4 = 8

Деление: Операция деления позволяет нам находить частное от деления одного натурального числа на другое. Частное является результатом деления. Например, если мы разделим число 10 на число 2, то получим частное равное 5.

Пример: 10 / 2 = 5

Возведение в степень: Операция возведения в степень позволяет нам получать результат, который получается при умножении натурального числа самого на себя заданное количество раз. Результат возведения в степень называется степенью. Например, если мы возводим число 2 в степень 3, то получим степень равную 8.

Пример: 23 = 8

Операции над множеством натуральных чисел являются основой для дальнейших математических вычислений и позволяют нам решать разнообразные задачи из разных областей науки и техники.

Примеры использования множества натуральных чисел

Математика

В математике множество натуральных чисел используется для изучения и доказательства различных теорем и свойств чисел. Например, с помощью натуральных чисел можно доказать бесконечность множества простых чисел или установить связь между простыми числами и делителями.

Арифметика

Множество натуральных чисел используется в арифметике для выполнения различных операций, таких как сложение, вычитание, умножение и деление. Оно позволяет осуществлять расчеты с целыми и дробными числами, а также решать уравнения и неравенства.

Компьютерные науки

В компьютерных науках множество натуральных чисел используется для решения различных задач, связанных с алгоритмами, структурами данных и программированием. Например, натуральные числа могут использоваться для создания циклов, индексации элементов массивов или определения количества итераций в алгоритмах.

Статистика

В статистике множество натуральных чисел используется для описания и анализа данных. Например, натуральные числа могут использоваться для подсчета количества наблюдений, построения гистограмм или определения вероятности событий.

Другие области

Множество натуральных чисел также находит применение в других областях, таких как физика, экономика, биология и т. д. В этих областях натуральные числа могут использоваться для моделирования явлений, описания закономерностей и прогнозирования результатов.

Таким образом, множество натуральных чисел является важным и неотъемлемым инструментом в математике и других научных дисциплинах, позволяющим решать разнообразные задачи и изучать свойства чисел и явлений.

Значимость множества натуральных чисел в математике

Во-первых, множество натуральных чисел позволяет считать и упорядочивать объекты. Оно используется для подсчета количества элементов в множестве и для определения порядка этих элементов.

Во-вторых, натуральные числа играют ключевую роль в арифметике. Они позволяют производить операции сложения, вычитания, умножения и деления, а также сравнивать числа между собой.

Кроме того, множество натуральных чисел обладает рядом важных свойств. Например, оно является бесконечным, то есть не имеет конечного предела. Каждое натуральное число имеет следующее число, которое на единицу больше, и предыдущее число, которое на единицу меньше. Это свойство позволяет использовать множество натуральных чисел для построения числовых систем.

Также множество натуральных чисел полезно для решения задач и построения моделей в различных областях науки, техники и экономики. Например, оно используется для описания количества объектов, времени, расстояния и других величин.

В заключение, множество натуральных чисел является одним из основных понятий математики. Оно имеет множество важных свойств и применений, и его изучение является неотъемлемой частью математического образования.

Вопрос-ответ:

Что такое множество натуральных чисел?

Множество натуральных чисел — это совокупность всех положительных целых чисел, начиная с 1.

Какие свойства имеет множество натуральных чисел?

Множество натуральных чисел обладает такими свойствами, как упорядоченность, бесконечность, замкнутость относительно сложения и умножения, а также отсутствие наименьшего элемента.

Можно ли множество натуральных чисел представить в виде диаграммы Эйлера-Венна?

Множество натуральных чисел нельзя представить в виде диаграммы Эйлера-Венна, так как оно бесконечно и не может быть указано в виде конечного набора элементов.

Есть ли в множестве натуральных чисел наименьший элемент?

В множестве натуральных чисел нет наименьшего элемента. Оно начинается с 1 и не имеет нижней границы.

Как множество натуральных чисел связано с другими множествами чисел?

Множество натуральных чисел является подмножеством множества целых чисел, рациональных чисел, вещественных чисел и комплексных чисел. Оно является основой для построения других множеств чисел.