Что относится к целым числам в математике

Целые числа — это числа, которые не имеют дробной или десятичной части. Они включают в себя натуральные числа, ноль и отрицательные числа. В математике целые числа используются для обозначения количества объектов или их положения на числовой оси. Узнайте больше о свойствах и операциях с целыми числами в математике.

Целые числа – это основная числовая система, которая включает в себя все натуральные числа, а также цифры, соответствующие отрицательным значениям. В математике они обозначаются символом Z и представляют собой бесконечную последовательность чисел, расположенных на числовой прямой.

Определение целых чисел включает в себя две категории: положительные и отрицательные числа. Положительные числа обозначаются без знака, а отрицательные числа – со знаком «минус». Число 0 также является целым числом и располагается в центре числовой прямой, разделяя положительные и отрицательные числа.

Примеры целых чисел:

• –3;
• –2;
• –1;
• 0;
• 1;
• 2;
• 3;

Целые числа являются основой для выполнения арифметических операций, таких как сложение, вычитание, умножение и деление. Они также используются во многих областях науки и повседневной жизни для описания и анализа различных явлений и процессов.

Что такое целые числа?

Целые числа состоят из двух групп: положительных и отрицательных чисел. Положительные целые числа — это числа, которые больше нуля и отмечаются без знака или со знаком «+». Отрицательные целые числа — это числа, которые меньше нуля и отмечаются со знаком «-«. Ноль является нейтральным числом и не относится ни к положительным, ни к отрицательным числам.

Например, в множестве целых чисел Z есть числа -3, -2, -1, 0, 1, 2, 3 и т.д. Эти числа могут быть использованы для измерения долга, температуры, времени и других физических величин.

Целые числа обладают рядом свойств и операций, которые позволяют выполнять арифметические операции с этими числами. Среди основных операций с целыми числами можно выделить сложение, вычитание, умножение и деление.

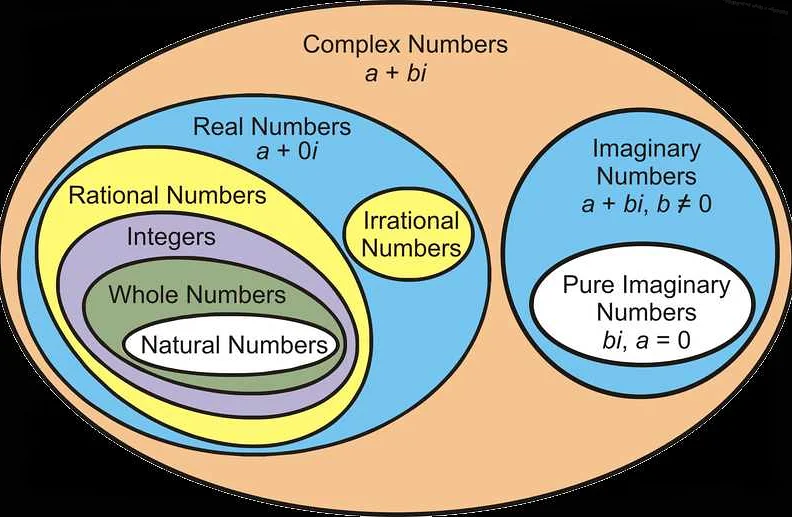
Целые числа являются основой для более сложных математических понятий, таких как рациональные числа, вещественные числа и комплексные числа. Изучение целых чисел позволяет понять основы математики и развить навыки аналитического мышления.

Определение целых чисел

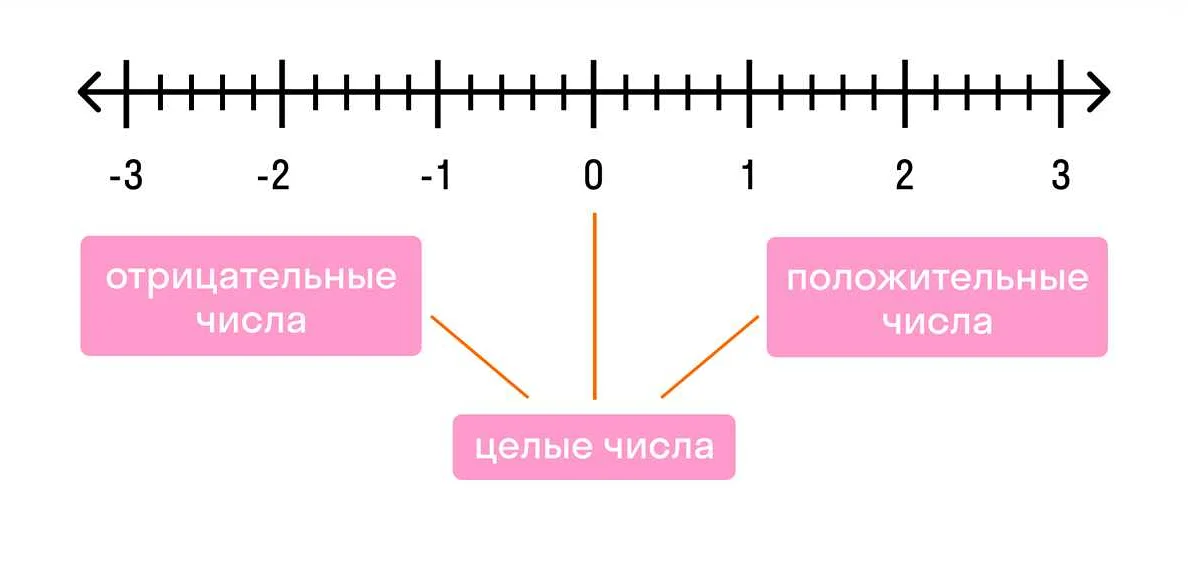
Набор целых чисел можно записать как {…, -3, -2, -1, 0, 1, 2, 3, …}.

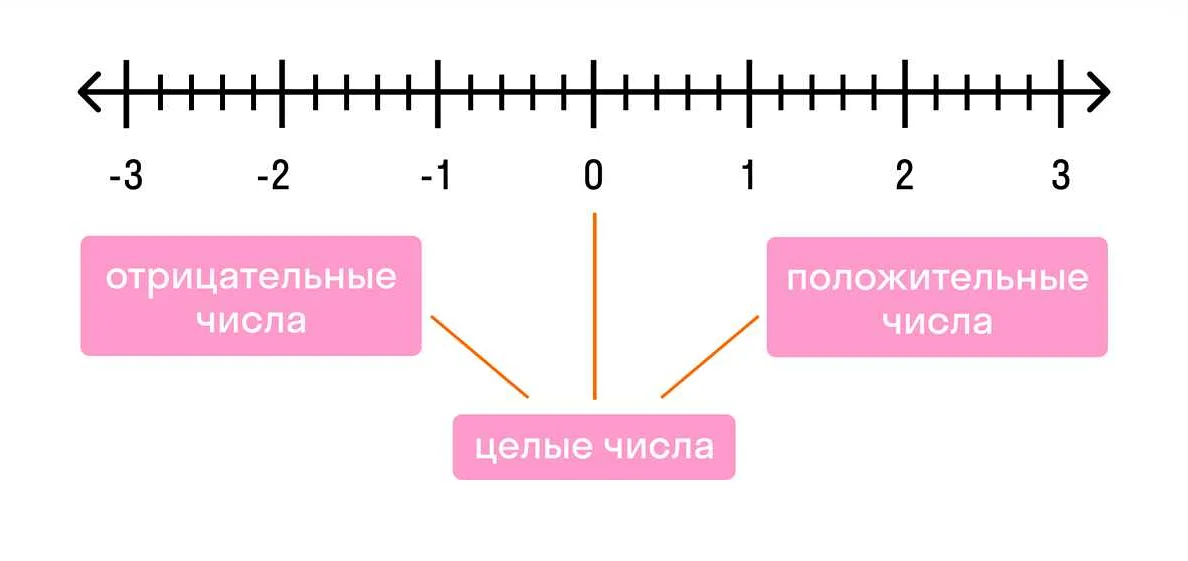
Каждое целое число может быть представлено на числовой оси, где положительные числа находятся справа от нуля, а отрицательные числа — слева от нуля. Такая числовая ось называется осью целых чисел.

Целые числа используются в различных областях математики и позволяют решать разнообразные задачи, связанные с отрицательными значениями, обратными операциями и алгоритмами, требующими целочисленных значений.

Примеры целых чисел: -5, -2, 0, 3, 10.

Свойства целых чисел

• Закон сложения: для любых двух целых чисел a и b, сумма a + b также является целым числом.
• Закон умножения: для любых двух целых чисел a и b, их произведение a * b также является целым числом.
• Закон коммутативности: при сложении и умножении целых чисел порядок слагаемых и множителей не имеет значения. То есть, a + b = b + a и a * b = b * a.
• Закон ассоциативности: при сложении и умножении целых чисел ассоциативный порядок слагаемых и множителей не имеет значения. То есть, (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c).
• Существование нейтральных элементов: для сложения существует нейтральный элемент 0, такой что a + 0 = a, а для умножения существует нейтральный элемент 1, такой что a * 1 = a.
• Закон дистрибутивности: умножение целых чисел распределено относительно сложения. То есть, a * (b + c) = (a * b) + (a * c).
• Существование противоположного элемента: для каждого целого числа a существует целое число -a, такое что a + (-a) = 0.

Эти свойства помогают нам работать с целыми числами и выполнять различные математические действия с ними.

Примеры целых чисел

Вот несколько примеров целых чисел:

1. 0 — нулевое целое число
2. 1 — положительное целое число
3. -1 — отрицательное целое число
4. 42 — положительное целое число
5. -100 — отрицательное целое число

Целые числа могут быть как положительными, так и отрицательными, а также включать в себя нуль.

Отрицательные целые числа

Отрицательные целые числа используются для обозначения долгов, убытков и других отрицательных величин. Они также являются частью числовой оси, которая представляет все возможные значения чисел.

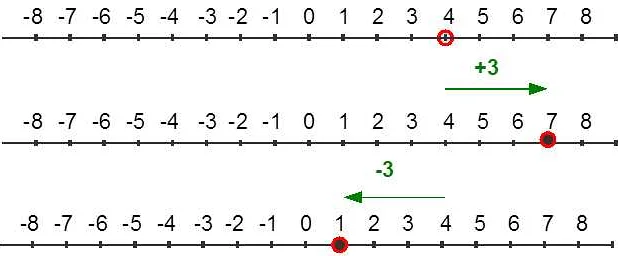
Для работы с отрицательными целыми числами используются различные математические операции, такие как сложение, вычитание, умножение и деление. Например, сумма двух отрицательных чисел будет отрицательной, а умножение отрицательного числа на положительное также даст отрицательный результат.

Отрицательные целые числа также могут быть представлены в виде десятичных дробей или десятичных чисел. Например, -1.5, -2.75 и так далее.

ПримерыОбъяснение

-5	Число -5 является отрицательным целым числом.
-10	Число -10 также является отрицательным целым числом.
-20	Число -20 тоже относится к отрицательным целым числам.

Отрицательные целые числа играют важную роль в математике и широко используются в различных областях, таких как финансы, физика, экономика и другие.

Положительные целые числа

Натуральные числа как подмножество целых чисел

Целые числа в математике включают в себя натуральные числа, а также их отрицательные значения и нуль. Натуральные числа представляют собой множество положительных целых чисел, начиная с единицы и продолжая до бесконечности.

Натуральные числаОбозначение

1	ℕ
2	ℕ
3	ℕ
4	ℕ
…	…

Натуральные числа обычно обозначаются символом «ℕ». Они используются в различных областях математики, физики и других наук для счета объектов, подсчета времени, измерения размеров и т.д. Например, натуральные числа можно использовать для подсчета количества яблок в корзине или для определения порядкового номера месяца в году.

Натуральные числа являются подмножеством целых чисел, так как включают только положительные значения, не включая отрицательные числа и ноль. При этом натуральные числа можно складывать, вычитать, умножать и делить друг на друга, получая другие натуральные числа или, при необходимости, отрицательные числа и ноль.

Итак, натуральные числа являются важной составляющей понятия целых чисел и используются для описания положительных значений и порядка объектов.

Вопрос-ответ:

Что такое целые числа в математике?

Целые числа в математике — это числа, которые включают в себя натуральные числа, отрицательные числа и ноль. Они образуют бесконечную числовую прямую.

Какие числа входят в понятие целых чисел?

В понятие целых чисел входят все натуральные числа (1, 2, 3, и так далее), их отрицательные значения (-1, -2, -3, и так далее) и ноль (0). Все они образуют бесконечное множество целых чисел.

Как можно представить целые числа на числовой прямой?

На числовой прямой целые числа представлены точками, которые расположены на равных расстояниях друг от друга. Нуль находится в центре прямой, положительные числа расположены справа от нуля, а отрицательные числа — слева.

Какие примеры целых чисел можно привести?

Примеры целых чисел: -3, -2, -1, 0, 1, 2, 3 и так далее. Все эти числа являются целыми, так как они включают нуль, положительные числа и отрицательные числа.

Какие операции можно выполнять с целыми числами?

С целыми числами можно выполнять все основные арифметические операции, такие как сложение, вычитание, умножение и деление. Также можно проводить сравнение чисел, находить их абсолютное значение и выполнять другие математические операции.

Целые числа и их применение в математике

Целые числа широко применяются в различных областях математики. Они используются для решения уравнений, вычисления и представления данных, анализа и моделирования. В математических операциях целые числа используются для сложения, вычитания, умножения, деления и других операций.

Примеры применения целых чисел:

• Финансовая математика: целые числа используются для подсчета доходов, расходов, прибыли и убытков.
• Графическое представление данных: целые числа могут быть использованы для отображения количественной информации на графиках и диаграммах.
• Криптография: целые числа используются для создания и анализа шифров и криптографических алгоритмов.

Целые числа играют важную роль в различных областях математики и имеют множество практических применений. Изучение целых чисел позволяет развить аналитическое мышление и навыки решения математических задач.

Видео по теме: