Что обозначает модуль в математике

Модуль в математике обозначает абсолютное значение числа или выражения. Он позволяет указать только величину числа, игнорируя его знак. Узнайте, как использовать модуль в различных математических задачах и формулах.

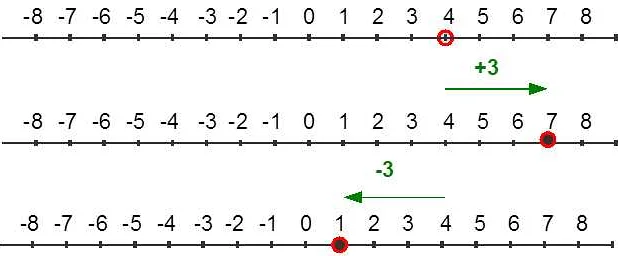
Модуль – это одно из базовых понятий в математике, которое используется для выражения абсолютной величины числа или выражения. Модуль числа a обозначается символом |a| и определяется как расстояние от числа a до нуля на числовой прямой. Другими словами, модуль числа показывает, насколько данное число отличается от нуля, без учета его знака.

Модуль может быть положительным или нулевым, если число или выражение имеют положительное значение, либо отрицательным, если число или выражение имеют отрицательное значение. Например, модуль числа 5 равен 5, а модуль числа -5 равен также 5.

Модуль активно применяется во многих областях математики и науки. Например, в физике он используется для измерения физических величин, таких как скорость, сила или энергия, а также для решения задач на определение расстояния или времени. В экономике модуль применяется для анализа экономических данных, таких как инфляция или безработица. В программировании модуль используется для работы с числами и вычислений.

Использование модуля в математике позволяет упростить вычисления и сделать их более точными. Он помогает избежать ошибок, связанных с учетом знаков и отрицательных значений. Благодаря модулю, проблемы, связанные с абсолютной величиной числа или выражения, могут быть легко решены.

Что такое модуль в математике?

Понятие модуля полезно, когда необходимо получить расстояние между двумя точками на числовой оси, независимо от их направления. Например, модуль от числа -5 будет равен 5, так как расстояние между числами -5 и 0 равно 5.

Модуль может быть использован для решения различных задач в математике и физике. Он помогает в нахождении расстояний, решении уравнений и неравенств, а также в анализе функций.

Значение числаМодуль

5	5
-5	5
0	0

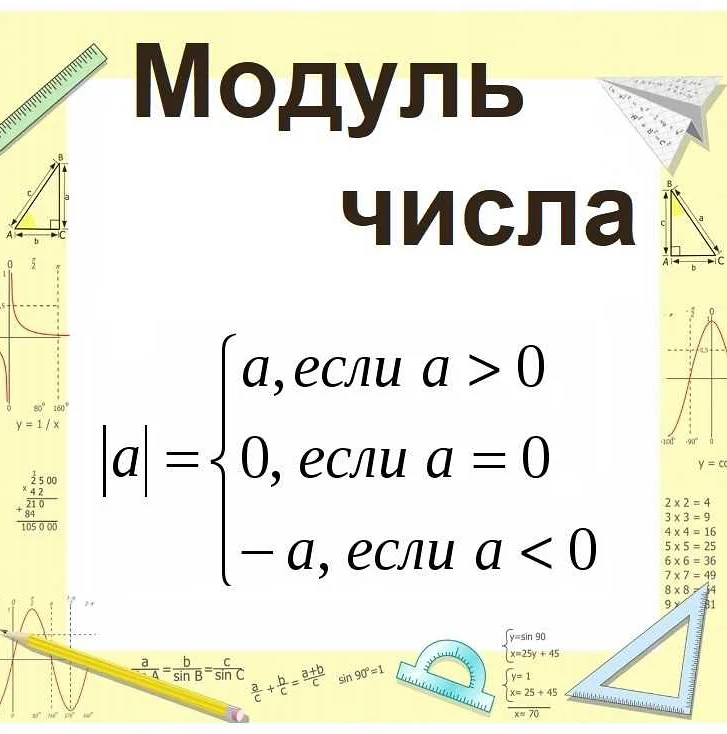
Определение модуля числа

Модуль числа обозначается символом |x|, где x — число.

Формально, модуль числа определяется следующим образом:

• Если x больше или равно нулю, то модуль числа равен самому числу: |x| = x.
• Если x меньше нуля, то модуль числа равен отрицательному значению числа: |x| = -x.

Например:

• Модуль числа 5 равен 5: |5| = 5.
• Модуль числа -3 равен 3: |-3| = 3.

Модуль числа используется в различных математических и физических задачах. Он позволяет учитывать только величину числа, а не его знак. Например, при расчетах скорости движения тела, мы не интересуемся его направлением, а только его величиной, и для этого используем модуль скорости.

Применение модуля в анализе данных

Одним из основных применений модуля в анализе данных является работа с отклонениями и ошибками. Например, при анализе результатов эксперимента или обработке статистических данных, может потребоваться вычислить абсолютное значение отклонения от истинного значения или среднего. Модуль позволяет получить положительное значение и удалить отрицательный знак, что упрощает анализ данных и сравнение результатов.

Еще одним применением модуля в анализе данных является работа с расстояниями и метриками. Например, при кластеризации данных или определении ближайших соседей в алгоритмах машинного обучения, может потребоваться вычислить расстояние между объектами. Модуль позволяет получить абсолютное значение расстояния, что необходимо для корректного сравнения и классификации данных.

Также модуль может использоваться для работы с функциями, которые могут принимать как положительные, так и отрицательные значения. Например, при оптимизации функции или нахождении ее минимума, модуль позволяет сосредоточиться только на числовых значениях, не учитывая их знаки.

В заключение можно сказать, что применение модуля в анализе данных позволяет упростить вычисления, убрать отрицательные знаки и сфокусироваться на числовых значениях. Это делает модуль важным инструментом для работы с данными и их анализа.

Модуль числа в геометрии

Модуль числа в геометрии обозначает расстояние от числа до начала координатной оси на числовой прямой. Он всегда является неотрицательным, то есть модуль отрицательного числа будет равен его положительному значению.

При решении геометрических задач модуль числа может быть использован для определения расстояния между двумя точками на плоскости или в пространстве. Также модуль числа может быть полезен при нахождении площади фигур или объема тел.

Например, модуль числа может быть использован для нахождения расстояния между двумя точками на плоскости. Если даны координаты точек A(x1, y1) и B(x2, y2), то расстояние между ними можно вычислить с помощью формулы:

d = √((x2 — x1)^2 + (y2 — y1)^2)

где d — расстояние между точками A и B.

Также модуль числа может быть применен для нахождения площади прямоугольника или треугольника. Например, площадь прямоугольника можно найти, зная длину его сторон a и b, с помощью формулы:

S = |a| * |b|

где S — площадь прямоугольника.

В заключение, модуль числа в геометрии является важным инструментом при решении геометрических задач и позволяет определить расстояние между точками, площадь фигур и другие параметры геометрических объектов.

Вычисление модуля в математических операциях

Для вычисления модуля числа используется следующая формула:

|x| =

• x, если x ≥ 0
• -x, если x < 0

Применение модуля в математических операциях широко распространено. Например, модуль используется для:

• Нахождения расстояния между двумя точками на числовой оси;
• Решения уравнений и неравенств;
• Нахождения максимального и минимального значения функции;
• Упрощения и сокращения выражений;
• Вычисления абсолютной разности между двумя числами и т.д.

Таким образом, модуль числа имеет важное значение в математике и находит свое применение во многих математических операциях и решениях задач.

Модуль в уравнениях и неравенствах

Модуль числа обозначается символом | | и используется для выражения расстояния от числа до нуля на числовой оси. Модуль всегда возвращает неотрицательное число, поэтому он удобно применяется в различных уравнениях и неравенствах.

В уравнениях с модулем мы ищем значения переменных, при которых модуль равен заданному числу. Например, уравнение |x| = 3 имеет два решения: x = 3 и x = -3, так как модуль числа 3 равен 3, а модуль числа -3 тоже равен 3.

В неравенствах с модулем мы ищем интервалы значений переменных, при которых модуль удовлетворяет условию. Например, неравенство |x| < 2 означает, что переменная x может принимать значения на интервале (-2, 2), исключая границы.

Модуль также может применяться для решения систем уравнений и неравенств. В этом случае каждое уравнение или неравенство с модулем разбивается на два уравнения или неравенства без модуля, которые затем решаются отдельно. Найденные решения объединяются в общее решение исходной системы.

Использование модуля в уравнениях и неравенствах позволяет учесть как положительные, так и отрицательные значения переменных, упрощает решение задач и дает более полное представление о возможных значениях переменных.

Модуль в теории вероятности

В теории вероятности модуль играет важную роль при расчете вероятностей событий. Модуль числа позволяет убрать отрицательные значения и рассматривать только положительные числа.

Модуль применяется, когда необходимо вычислить вероятность события, независимо от его направления или знака. Например, при расчете вероятности попадания в цель при стрельбе, модуль используется для исключения отрицательных значений, таких как недостаточное количество пулек или неправильное направление выстрела.

Модуль также может использоваться для определения расстояния между двумя значениями в теории вероятности. Например, при оценке вероятности попадания в мишень при стрельбе с различных расстояний, модуль может быть использован для вычисления абсолютного значения разности между текущим расстоянием и желаемым расстоянием до мишени.

Использование модуля в теории вероятности позволяет упростить расчеты и сделать их более наглядными. Он помогает исключить отрицательные значения и фокусироваться только на положительных величинах, что упрощает анализ и понимание вероятностных распределений.

Вопрос-ответ:

Что такое модуль в математике?

Модуль в математике — это числовая функция, которая возвращает абсолютное значение числа. Она показывает, насколько число отличается от нуля и всегда возвращает положительное значение.

Какая формула используется для вычисления модуля числа?

Для вычисления модуля числа используется следующая формула: если число положительное или равно нулю, то модуль равен самому числу; если число отрицательное, то модуль равен этому числу со знаком минус.

Зачем нужен модуль в математике?

Модуль в математике имеет множество применений. Он используется для нахождения расстояния между двумя точками на числовой прямой, для определения величины отклонения, для нахождения максимального или минимального значения из нескольких чисел и многое другое.

Как модуль помогает в решении математических задач?

Модуль помогает в решении математических задач, где важно определить величину, независимую от знака числа. Например, при работе с расстояниями или при нахождении максимального или минимального значения. Он также используется для упрощения выражений и упрощения вычислений.

Как модуль влияет на графики функций?

Модуль влияет на графики функций, так как он определяет абсолютное значение функции и игнорирует ее знак. Например, график функции модуля y = |x| будет всегда находиться выше оси x и будет симметричен относительно оси y. Это позволяет анализировать функции и исследовать их свойства.

Что такое модуль в математике?

Модуль числа — это число без знака, то есть модуль отрицательного числа равен его абсолютной величине.

Зачем нужен модуль в математике?

Модуль числа используется для нахождения абсолютной величины числа, независимо от его знака. Он также применяется в решении уравнений, нахождении расстояния между точками и во многих других математических задачах.

Видео по теме: