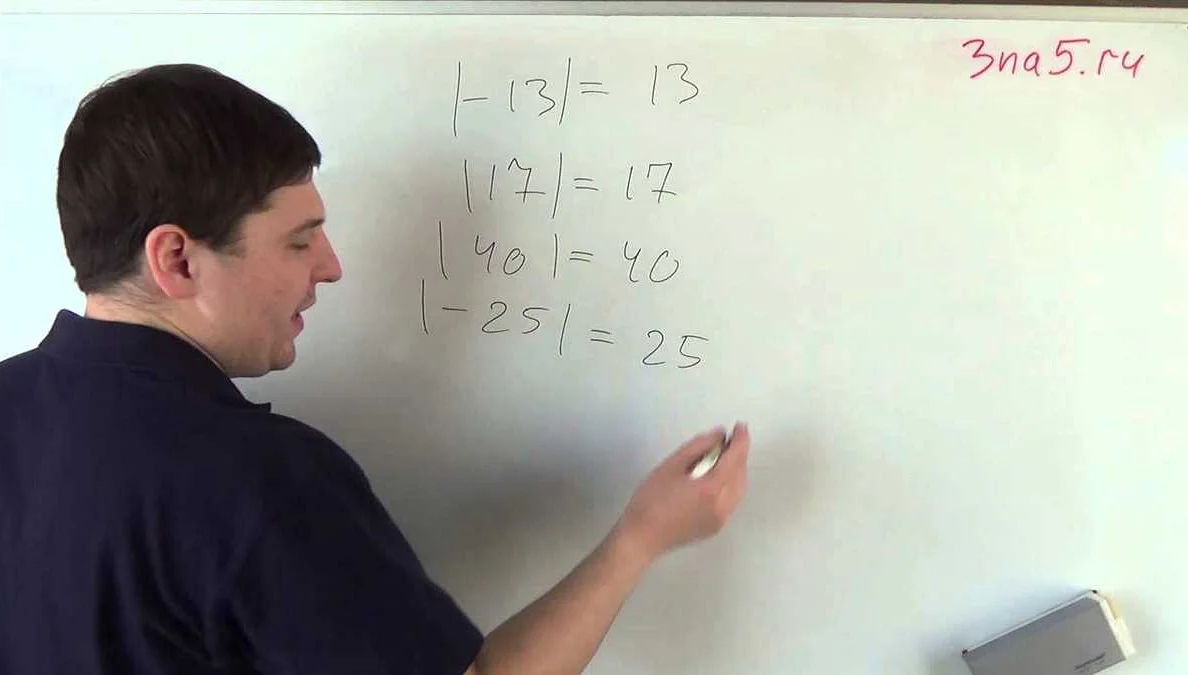Что означает слово модуль в математике

Модуль в математике — это функция, которая возвращает положительное значение числа без учета его знака. Узнайте, как работает модуль и для чего он используется в различных математических операциях.

Модуль — одно из основных понятий в математике, которое широко применяется в различных областях. Понятие модуля возникает из необходимости измерить расстояние между двумя точками на числовой прямой, и оно позволяет работать с отрицательными числами без учета их знака.

Модуль числа обозначается символом |x| и определяется как расстояние от нуля до этого числа на числовой прямой. В случае положительного числа модуль равен самому числу, а для отрицательного числа модуль равен его модулю с противоположным знаком. Например, модуль числа -5 равен 5, а модуль числа 3 равен 3.

Модуль числа имеет несколько свойств, которые позволяют использовать его в различных задачах. Во-первых, модуль всегда неотрицателен, то есть он всегда больше или равен нулю. Во-вторых, модуль отрицательного числа равен модулю этого числа с противоположным знаком. Кроме того, модуль суммы двух чисел не превосходит суммы модулей этих чисел.

Примеры использования модуля в математике включают нахождение расстояния между двумя точками на плоскости, решение уравнений и неравенств, а также определение экстремальных значений функций. Модуль также широко используется в компьютерной графике и физике для измерения величин и работы с отрицательными числами.

Что такое модуль в математике: понятие и свойства

Основное свойство модуля заключается в том, что модуль любого числа всегда неотрицателен: |a| ≥ 0.

Если число a положительное, то его модуль равен самому числу: |a| = a.

Если число a отрицательное, то его модуль равен числу с обратным знаком: |a| = -a.

Модуль числа можно использовать для решения различных задач и упрощения математических вычислений. Например, модуль числа может использоваться для определения расстояния между двумя точками на числовой оси или для нахождения абсолютного значения выражения.

В математических операциях с модулем числа применяются следующие свойства:

• Свойство модуля суммы: |a + b| ≤ |a| + |b|.
• Свойство модуля произведения: |a * b| = |a| * |b|.
• Свойство модуля квадратного корня: |√a| = √(a^2).

Использование модуля в математике позволяет более гибко работать с числами и упрощает решение различных задач.

Определение модуля

Формально, модуль числа x определяется следующим образом:

Если x ≥ 0	то |x| = x
Если x < 0	то |x| = -x

Таким образом, модуль числа всегда положительный или нулевой.

На практике модуль числа часто используется для измерения расстояний и величин, игнорируя их направление или знак.

Например:

• Модуль числа -5 равен 5, так как -5 < 0.
• Модуль числа 3 равен 3, так как 3 ≥ 0.

Свойства модуля

Модуль числа обладает несколькими свойствами, которые делают его полезным и удобным понятием в математике:

Свойство	Описание
1. Абсолютная величина	Модуль числа всегда является неотрицательным числом. Это значит, что независимо от знака числа, его модуль будет положительным или равным нулю.
2. Связь с алгебраическими операциями	Модуль числа можно использовать в алгебраических операциях, таких как сложение и вычитание. Например, модуль суммы двух чисел будет меньше или равен сумме их модулей.
3. Геометрическое значение	В геометрии модуль числа обычно интерпретируется как расстояние от числа до нуля на числовой прямой. Это позволяет использовать модуль в решении задач, связанных с расстояниями.
4. Неравенство треугольника	Модуль числа удовлетворяет неравенству треугольника, которое гласит: модуль суммы двух чисел меньше или равен сумме их модулей. Это свойство является основой для доказательств и решения различных задач.
5. Разделение числовой прямой	Модуль числа позволяет разделить числовую прямую на отрезки, например, положительные и отрицательные числа. Такая классификация упрощает работу с числами и их сравнение.

Это лишь некоторые из свойств модуля числа, которые делают его полезным инструментом в математике. Знание этих свойств позволяет более глубоко понять и использовать модуль в различных математических задачах.

Модуль числа и его значения

Модуль числа в математике представляет собой неотрицательное значение числа, независимо от его знака. Модуль числа обозначается символом «|» и ставится перед числом, для которого нужно найти модуль. Например, модуль числа -5 обозначается как |-5| = 5.

Основное свойство модуля числа заключается в том, что он всегда возвращает положительное число или ноль. Независимо от того, является ли исходное число отрицательным или положительным, его модуль всегда будет положительным.

Использование модуля числа широко распространено в различных областях математики и ее приложениях. Например, модуль числа может использоваться для нахождения расстояния между двумя точками на числовой оси. Если есть две точки с координатами a и b, то расстояние между ними можно найти как |b — a|.

Модуль числа также используется для решения уравнений и неравенств. Например, при решении уравнения |x — 3| = 5 нужно найти такие значения x, для которых модуль разности x и 3 равен 5. В данном случае возможны два решения: x = -2 и x = 8.

Кроме того, модуль числа может использоваться для определения абсолютной величины, то есть для нахождения величины по модулю. Например, модуль числа -7 равен 7, что можно интерпретировать как абсолютное значение числа -7.

Таким образом, модуль числа является важным понятием в математике, которое позволяет найти неотрицательное значение числа, независимо от его знака. Он имеет множество применений в различных математических задачах и позволяет решать уравнения, находить расстояния и определять абсолютные значения чисел.

Модуль и арифметические операции

Модуль числа можно рассматривать как расстояние от нуля до этого числа на числовой прямой. Например, модуль числа -5 равен 5, так как расстояние от -5 до 0 равно 5.

Модуль может быть выражен с помощью абсолютного значения числа. Абсолютное значение числа – это число без знака. Например, абсолютное значение числа -5 равно 5.

Модуль числа можно использовать при выполнении арифметических операций. Рассмотрим несколько примеров:

Пример 1: Вычисление модуля суммы двух чисел.

Даны числа a и b. Найдем модуль их суммы: |a + b|.

Например, пусть a = 3 и b = -2. Тогда сумма a + b = 3 + (-2) = 1. Модуль числа 1 равен 1. Таким образом, модуль суммы чисел 3 и -2 равен 1.

Пример 2: Вычисление модуля разности двух чисел.

Даны числа a и b. Найдем модуль их разности: |a — b|.

Например, пусть a = 5 и b = 8. Тогда разность a — b = 5 — 8 = -3. Модуль числа -3 равен 3. Таким образом, модуль разности чисел 5 и 8 равен 3.

Пример 3: Вычисление модуля произведения двух чисел.

Даны числа a и b. Найдем модуль их произведения: |a * b|.

Например, пусть a = -4 и b = 6. Тогда произведение a * b = (-4) * 6 = -24. Модуль числа -24 равен 24. Таким образом, модуль произведения чисел -4 и 6 равен 24.

Таким образом, модуль числа позволяет получить числовое значение без учета его знака и может использоваться при выполнении различных арифметических операций.

Модуль и неравенства

Модуль числа a равен a, если a ≥ 0, и -a, если a < 0.

Модули чисел широко используются при решении неравенств. Для начала рассмотрим неравенства с одной переменной. Пусть a и b – два числа. Неравенство |a| < b выполняется, если a лежит в интервале (-b, b). Если же неравенство |a| > b, то a лежит вне интервала (-b, b).

Важно отметить, что неравенство |a| < b эквивалентно двум неравенствам a < b и -a < b. Неравенство |a| > b, в свою очередь, эквивалентно двум неравенствам a > b и -a > b.

Рассмотрим пример использования модуля и неравенств. Допустим, необходимо решить неравенство |3x — 2| ≤ 5. Для начала, разобьем это неравенство на два: 3x — 2 ≤ 5 и 3x — 2 ≥ -5. Решив каждое из них отдельно, получим x ≤ 7/3 и x ≥ -1.

НеравенствоРешение

3x — 2 ≤ 5	x ≤ 7/3
3x — 2 ≥ -5	x ≥ -1

Видео по теме:

Вопрос-ответ:

Что такое модуль?

Модуль числа — это его абсолютное значение, то есть число без знака. Например, модуль числа -5 равен 5, а модуль числа 7 равен 7.

Зачем нужен модуль в математике?

Модуль используется для измерения расстояния между числами, независимо от их положительности или отрицательности. Он также позволяет найти абсолютное значение числа, что может быть полезно при решении задач и уравнений.

Как вычислить модуль числа?

Чтобы вычислить модуль числа, нужно взять его абсолютное значение. Если число положительное, то модуль равен самому числу. Если число отрицательное, то модуль равен числу с противоположным знаком. Например, модуль числа -6 равен 6, а модуль числа 9 равен 9.

Какие свойства имеет модуль числа?

Модуль числа обладает несколькими свойствами. Например, модуль произведения двух чисел равен произведению модулей этих чисел. Также модуль суммы двух чисел не превышает суммы их модулей. Кроме того, модуль разности двух чисел не превышает разности их модулей.

Как модуль используется в практических задачах?

Модуль используется в различных ситуациях. Например, он может использоваться для определения расстояния между двумя точками на числовой оси, для нахождения наименьшего или наибольшего значения функции, для определения модуля разности двух значений и т.д. Примеры использования модуля в математике есть как в теории, так и в практике.

Что такое модуль числа?

Модуль числа — это его абсолютное значение, то есть расстояние от нуля на числовой оси. Например, модуль числа -5 равен 5, модуль числа 3 равен 3.

Модуль и системы координат

Модуль может быть положительным или нулевым, если число больше или равно нулю, или отрицательным, если число меньше нуля. Например, модуль числа 5 равен 5, а модуль числа -5 также равен 5.

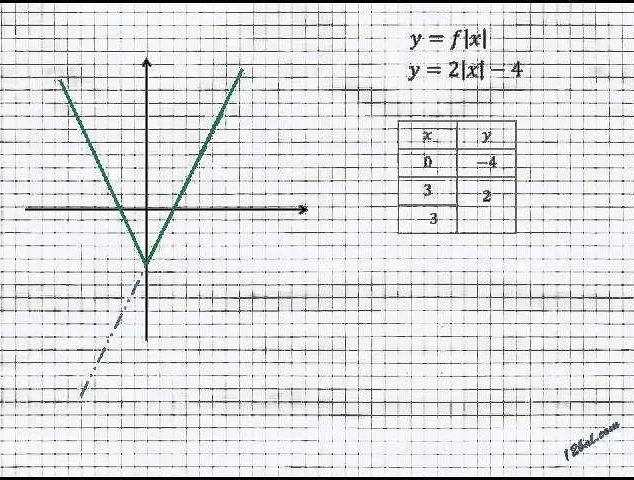
Модуль можно представить геометрически с помощью систем координат. На плоскости система координат состоит из двух осей: горизонтальной оси x и вертикальной оси y. Числа, отображаемые на оси x, называются абсциссами, а числа, отображаемые на оси y, называются ординатами. Точка, в которой пересекаются оси x и y, называется началом координат и обозначается буквой O.

Модуль числа a можно представить как расстояние от точки на числовой оси до начала координат. Если a положительное число, то модуль a равен расстоянию от a до O. Если a отрицательное число, то модуль a равен расстоянию от a до O, но с противоположным знаком. Например, модуль числа -5 равен 5, так как расстояние от -5 до O равно 5.

Модуль часто используется при решении задач на нахождение расстояния между точками, скорости тела, а также при работе с комплексными числами.

ЧислоМодуль

5	5
-5	5
0	0

Примеры использования модуля в математике

• Определение расстояния: модуль может использоваться для определения расстояния между двумя точками на числовой оси. Например, для точек A и B на числовой оси, расстояние между ними можно выразить как |A — B|.
• Нахождение абсолютной величины: модуль может использоваться для определения абсолютной величины числа. Например, модуль числа -5 равен 5, так как его абсолютная величина всегда положительна.
• Решение уравнений: модуль может использоваться для решения уравнений с модулем. Например, модульное уравнение |x — 2| = 3 имеет два решения: x = 5 и x = -1.
• Определение окружности: модуль может использоваться для определения окружности с центром в заданной точке и заданного радиуса. Например, окружность с центром в точке (2, 3) и радиусом 4 может быть определена с помощью модуля как { (x, y) | |x — 2| + |y — 3| = 4 }.

Это лишь некоторые примеры использования модуля в математике. Общим свойством всех этих примеров является использование модуля для измерения расстояния, определения абсолютной величины или решения уравнений. Модуль играет важную роль в математических вычислениях и может быть использован в различных областях, включая геометрию, анализ и алгебру.