Что такое мощность множества в математике

Мощность множества в математике — это количество элементов, содержащихся в данном множестве. Узнайте, как определять мощность множества и как она связана с понятием бесконечности. Изучите основные свойства мощности множеств и примеры ее применения в различных областях математики.

Мощность множества является одним из основных понятий в математике. Она позволяет измерить количество элементов в данном множестве. Мощность множества может быть конечной или бесконечной, что зависит от количества элементов в нем.

Конечная мощность множества определяется числом элементов, которые входят в это множество. Например, множество {1, 2, 3} содержит три элемента, поэтому его мощность равна трем. Также существуют пустые множества, которые не содержат ни одного элемента. Их мощность равна нулю.

Бесконечная мощность множества может быть определена с помощью различных методов. Например, можно сравнить мощности двух множеств и выяснить, является ли одно из них более «крупным» по количеству элементов, чем другое. Если не существует взаимно-однозначного соответствия между элементами двух множеств, то они имеют различные мощности.

Примером бесконечно мощного множества является множество всех натуральных чисел. Оно обозначается символом N. В нем содержится бесконечное количество элементов, поэтому его мощность равна бесконечности.

Также существуют множества с континуальной мощностью, которые находятся между конечными и бесконечными множествами. Они имеют мощность, равную мощности множества действительных чисел и обозначаются символом C.

Мощность множества является фундаментальным понятием в математике и находит применение во многих ее областях. Она позволяет строить сложные модели и решать различные задачи, связанные с количеством элементов в множествах. Понимание и умение работать с мощностью множества является важным навыком для математика и других специалистов в этой области.

Что такое мощность множества?

Для конечных множеств мощность определяется простым подсчетом количества элементов. Например, мощность множества {1, 2, 3} равна 3, так как в нем содержатся три элемента.

Для бесконечных множеств мощность определяется с помощью специальных инструментов и методов. Например, мощность множества всех натуральных чисел (обозначается как N) является бесконечной. Это можно объяснить тем, что натуральных чисел несчетно много и их нельзя перечислить в конечном списке.

Мощность множества может быть также меньше или равной нулю. Например, пустое множество (множество, не содержащее ни одного элемента) имеет мощность 0.

Мощность множества имеет важное значение в различных областях математики, таких как теория множеств, теория вероятностей, алгебра и другие. Она позволяет формально описывать и изучать свойства множеств и их отношения.

Как измерить мощность множества?

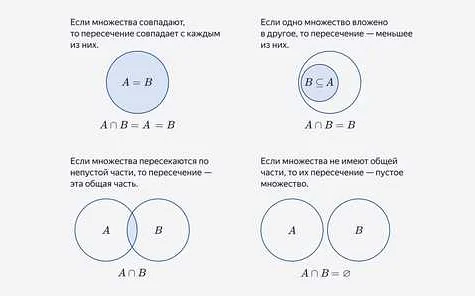
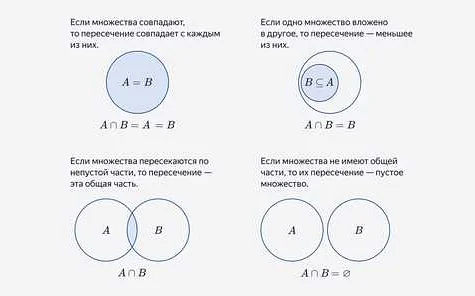
1. Считать элементы множества вручную. Этот метод применим для небольших множеств, когда элементы можно перечислить и посчитать число элементов.

Пример:

Множество A = {1, 2, 3, 4, 5}

Мощность множества A равна 5, так как в нем содержатся 5 элементов.

2. Использовать кардинальное число множества. Кардинальное число множества — это число, которое указывает на количество элементов в данном множестве. Для конечных множеств это число называется конечным кардинальным числом, для бесконечных множеств — бесконечным кардинальным числом.

Пример:

Конечное множество A = {1, 2, 3, 4, 5}

Конечное кардинальное число множества A равно 5.

3. Использовать функцию мощности множества. Функция мощности множества — это математическая функция, которая принимает множество в качестве аргумента и возвращает его мощность. В программировании такая функция может называться, например, len(), если мы говорим о мощности списка или строки.

Пример:

Множество A = {1, 2, 3, 4, 5}

Мощность множества A равна len(A), то есть 5.

Таким образом, мощность множества можно измерить путем перечисления его элементов и подсчета их числа, использования кардинального числа или функции мощности множества.

Примеры мощности множеств

В математике существует несколько примеров, демонстрирующих различные мощности множеств. Некоторые из них включают:

1. Множество натуральных чисел (N) имеет бесконечную мощность. Это означает, что его элементы невозможно перечислить один за другим, поскольку они продолжаются в бесконечность.
2. Множество целых чисел (Z) также имеет бесконечную мощность, так как оно включает в себя как положительные, так и отрицательные числа.
3. Множество действительных чисел (R) также имеет бесконечную мощность. Оно включает в себя все возможные десятичные дроби, а также иррациональные числа, такие как корень из 2 или число π.
4. Множество комплексных чисел (C) также имеет бесконечную мощность. Комплексные числа представляются в виде a + bi, где a и b — это действительные числа, а i — мнимая единица.
5. Множество рациональных чисел (Q) имеет счетную мощность, что означает, что его элементы можно упорядочить и пронумеровать. Рациональные числа — это числа, которые могут быть представлены в виде обыкновенной дроби.

Это лишь несколько примеров, и в математике существует множество других мощностей множеств. Изучение мощности множеств позволяет нам понять, какие множества более «большие» или «меньшие» других и как их сравнивать.

Мощность конечного множества

Для вычисления мощности конечного множества необходимо перечислить все его элементы и посчитать их количество. Например, рассмотрим множество цветов светофора: {красный, желтый, зеленый}. Оно содержит 3 элемента, поэтому его мощность равна 3.

Еще один пример — множество дней недели: {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}. Оно содержит 7 элементов, поэтому его мощность равна 7.

МножествоЭлементыМощность

Цвета светофора	красный, желтый, зеленый	3
Дни недели	понедельник, вторник, среда, четверг, пятница, суббота, воскресенье	7

Таким образом, мощность конечного множества можно определить путем подсчета количества его элементов. Это позволяет нам увидеть, сколько элементов содержится в данном множестве и сравнить его с другими множествами.

Мощность бесконечного множества

Бесконечные множества могут иметь различные мощности, и их сравнение требует применения специальных инструментов и концепций, таких как кардинальные числа и теория множеств.

Одним из примеров бесконечного множества является множество натуральных чисел. Это множество обозначается как N и содержит все положительные целые числа, начиная с 1. Мощность множества натуральных чисел считается счетной, и обозначается символом ℕ₀. Это означает, что мощность множества натуральных чисел можно сопоставить с мощностью множества натуральных чисел.

Однако, есть бесконечные множества, мощность которых больше, чем мощность множества натуральных чисел. Например, множество всех вещественных чисел обозначается как R. Мощность множества вещественных чисел больше, чем мощность множества натуральных чисел, и обозначается символом ℕ. Это означает, что мощность множества вещественных чисел нельзя сопоставить с мощностью множества натуральных чисел.

Бесконечные множества могут иметь разные мощности, и их сравнение с помощью кардинальных чисел является важной задачей в теории множеств. Это позволяет определить, насколько одно бесконечное множество «больше» или «меньше» другого.

Таким образом, мощность бесконечного множества зависит от его внутренней структуры и может быть определена с помощью специальных инструментов и концепций теории множеств.

Мощность подмножества

Мощность подмножества определяется как количество элементов, содержащихся в данном подмножестве. Если мощность исходного множества равна n, то количество подмножеств равно 2^n.

Для примера рассмотрим множество A = {1, 2, 3}. В данном случае мощность исходного множества равна 3. Соответственно, количество подмножеств будет равно 2^3 = 8. Полный перечень подмножеств множества A будет следующим: {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}.

Мощность подмножества может быть равна и нулю, в случае если в подмножестве не содержится ни одного элемента. Такое подмножество называется пустым и обозначается символом {}.

Для описания мощности подмножеств часто используется таблица. В таблице указываются все возможные подмножества и их мощность.

ПодмножествоМощность

{}	0
{1}	1
{2}	1
{3}	1
{1, 2}	2
{1, 3}	2
{2, 3}	2
{1, 2, 3}	3

Как видно из таблицы, сумма мощностей всех подмножеств равна мощности исходного множества.

Мощность объединения множеств

Мощность объединения двух множеств определяется как количество элементов, содержащихся в объединении этих множеств.

Для двух конечных множеств A и B мощность их объединения обозначается как |A ∪ B|. Если множества A и B имеют m и n элементов соответственно, то мощность объединения будет равна m + n минус количеству элементов, которые присутствуют в обоих множествах одновременно.

Мощность объединения множеств может быть меньше суммы мощностей самих множеств, так как некоторые элементы могут дублироваться в объединении.

Например, пусть A = {1, 2, 3} и B = {3, 4, 5}. Мощность объединения множеств A и B будет равна 5, так как в объединении присутствуют элементы {1, 2, 3, 4, 5}. Заметим, что элемент 3 встречается в обоих множествах, поэтому его нужно учесть только один раз.

Таким образом, мощность объединения множеств является важным понятием в теории множеств и может быть использована для решения различных задач.

Вопрос-ответ:

Что такое мощность множества?

Мощность множества — это количество элементов, находящихся в данном множестве. Она позволяет оценить размер и разнообразие элементов в множестве.

Как определить мощность множества?

Мощность множества можно определить с помощью кардинального числа, которое обозначает количество элементов в множестве. Например, если множество содержит 5 элементов, то его мощность будет равна 5.

Какие примеры мощности множества можно привести?

Примеры мощности множества могут быть разнообразными. Например, множество натуральных чисел имеет бесконечную мощность, в то время как множество целых чисел имеет также бесконечную мощность, но большую, чем у натуральных чисел. Другой пример — множество всех букв алфавита имеет мощность 26, так как алфавит состоит из 26 букв.

Как мощность множества связана с теорией множеств?

Мощность множества играет важную роль в теории множеств. Она позволяет сравнивать и классифицировать множества по их размеру. Например, с помощью мощности можно определить, является ли множество конечным или бесконечным, и сравнить размеры различных бесконечных множеств.

Мощность декартова произведения множеств

Декартово произведение двух множеств A и B состоит из всех упорядоченных пар, где первый элемент принадлежит множеству A, а второй — множеству B. Если множества A и B содержат n и m элементов соответственно, то мощность декартова произведения будет равна n × m.

Например, пусть A = {1, 2, 3} и B = {a, b}. Декартово произведение A × B будет состоять из следующих пар: (1, a), (1, b), (2, a), (2, b), (3, a), (3, b). В данном случае множество A содержит 3 элемента, а множество B — 2 элемента. Следовательно, мощность декартова произведения A × B будет равна 3 × 2 = 6.

ABA × B

1	a	(1, a)
1	b	(1, b)
2	a	(2, a)
2	b	(2, b)
3	a	(3, a)
3	b	(3, b)

Видео по теме: