Что такое обозначение углов в математике

Обозначение углов в математике представляет собой способ указания меры или положения угла с помощью символов, линий и цифр. Углы обозначаются буквами, как правило, латинского алфавита, и сопровождаются индексами и знаками, которые указывают на их свойства, такие как прямой, тупой, острый и др. Понимание обозначения углов позволяет более точно описывать и рассчитывать их свойства и взаимное расположение.

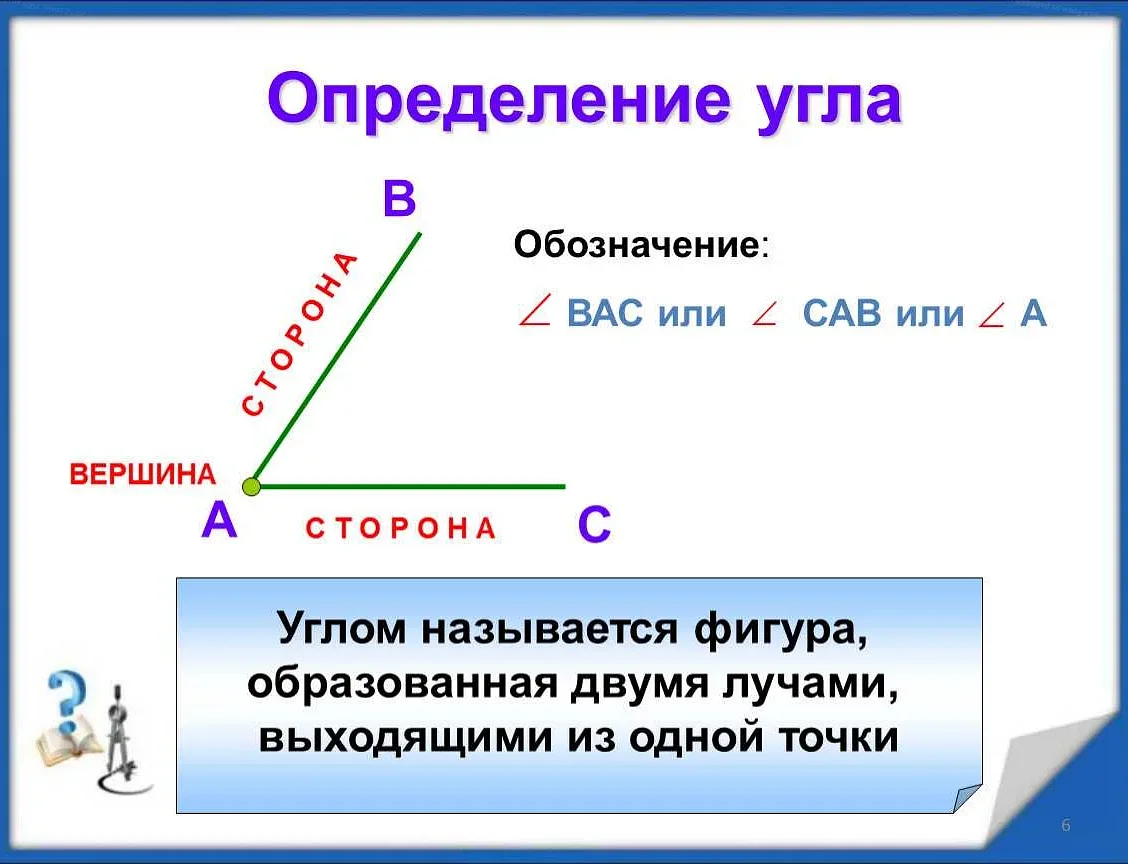
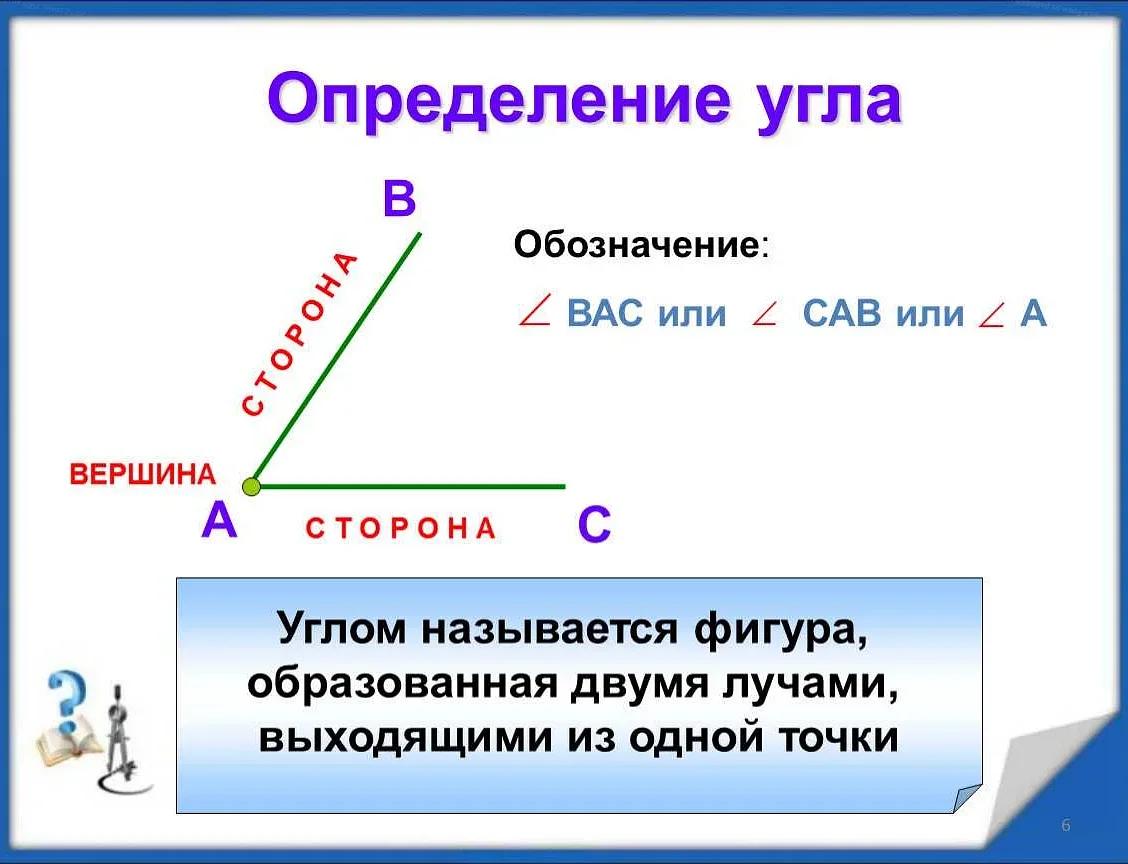
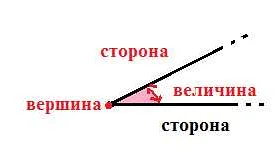
Угол — это геометрическая фигура, образованная двумя лучами, исходящими из одной точки, называемой вершиной угла. В математике углы играют важную роль и широко применяются в различных областях, таких как геометрия, физика, астрономия и др.

Обозначение углов в математике происходит с использованием специальных символов. Основными символами обозначения углов являются греческие буквы: α (альфа), β (бета), γ (гамма) и их заглавные варианты: Α, Β, Γ.

Например, угол может быть обозначен символом α, а прямой угол — символом γ. Также можно использовать комбинацию букв и цифр для обозначения углов, например, α1, β2 или γ3.

Кроме того, для обозначения углов можно использовать и другие символы, такие как знаки ° (градус), ‘ (минута) и » (секунда). Например, угол может быть обозначен как 45°, 30’, 15″. Такое обозначение используется чаще всего в геодезии и астрономии для измерения угловых величин.

Угол: определение и свойства

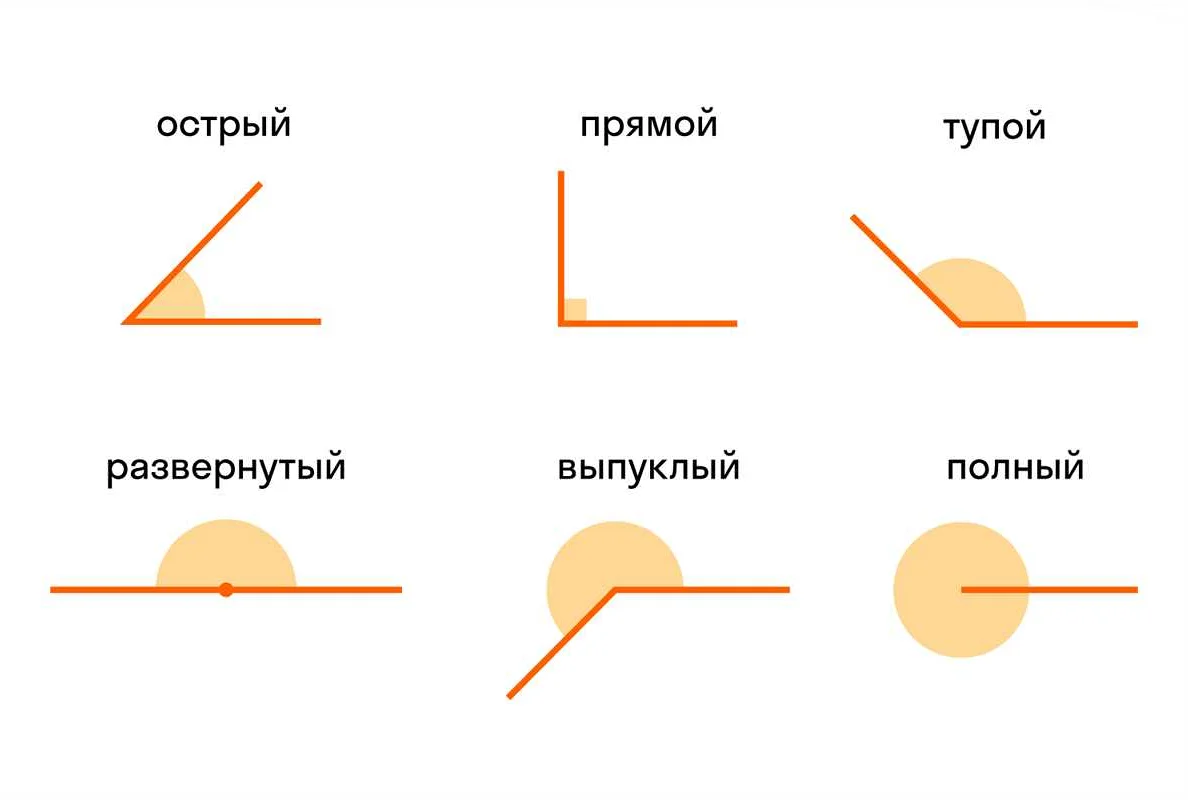
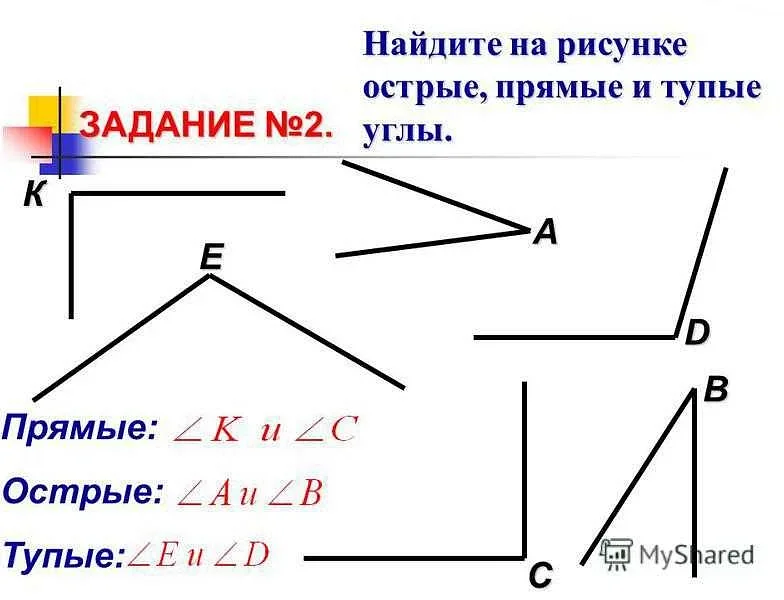
Углы могут быть различных типов, в зависимости от их величины:

• Острый угол — угол, значение которого меньше 90 градусов;
• Прямой угол — угол, значение которого равно 90 градусам;
• Тупой угол — угол, значение которого больше 90 градусов, но меньше 180 градусов;
• Развернутый угол — угол, значение которого равно 180 градусам;
• Рефлексивный угол — угол, значение которого больше 180 градусов, но меньше 360 градусов.

Кроме того, углы могут быть смежными, вертикальными, суплементарными и комплиментарными:

• Смежные углы — углы, имеющие общую сторону и общую вершину, но не пересекающиеся;
• Вертикальные углы — пара углов, образованная пересекающимися прямыми и имеющая равные значения;
• Суплементарные углы — пара углов, сумма которых равна 180 градусов;
• Комплиментарные углы — пара углов, сумма которых равна 90 градусов.

Знание свойств и определений углов является важной основой для решения задач и построения геометрических фигур.

Видео по теме:

Виды углов по величине

Углы можно классифицировать по величине на следующие виды:

1. Острые углы – это углы, которые меньше 90 градусов. Например, угол в 60 градусов будет острым углом.

2. Прямой угол – угол, который равен 90 градусов. Прямой угол можно наблюдать, например, в угле стола или в углу прямоугольного листа бумаги.

3. Тупой угол – угол, который больше 90 градусов, но меньше 180 градусов. Примером тупого угла может служить угол в 120 градусов.

4. Разносторонний угол – угол, который равен 180 градусов. Это полный оборот или прямая линия.

Все углы в данных классификациях измеряются в градусах и являются основными видами углов по величине.

Виды углов по положению сторон

Углы по положению сторон могут быть разделены на следующие виды:

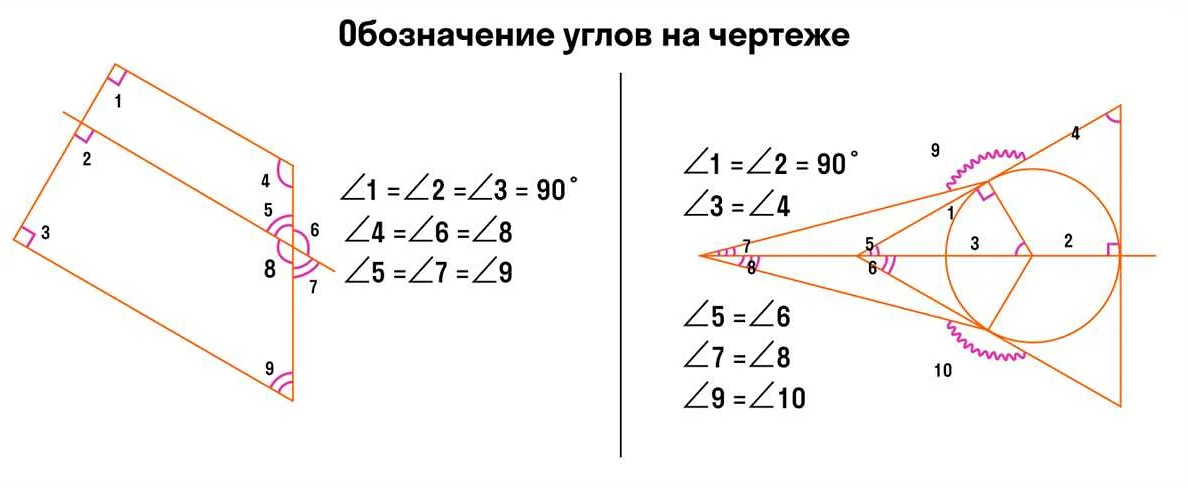
Вид углаОписаниеПример

Острый угол	Угол, значение которого меньше 90 градусов.
Прямой угол	Угол, значение которого равно 90 градусов.
Тупой угол	Угол, значение которого больше 90 градусов, но меньше 180 градусов.
Развернутый угол	Угол, значение которого равно 180 градусов.
Отрицательный угол	Угол, значение которого отрицательно и меньше -180 градусов.

Знание этих видов углов помогает в анализе и решении различных задач в геометрии и физике.

Вопрос-ответ:

Что такое угол в математике?

Угол в математике — это геометрическая фигура, образованная двумя лучами, исходящими из одной точки, которая называется вершиной угла. Углы могут быть измерены в градусах, радианах или градусно-минутно-секундных делениях.

Как обозначаются углы в математике?

Углы в математике обычно обозначаются тремя буквами, причем средняя буква находится внутри угла и обозначает саму вершину. Например, угол ABC означает угол, у которого вершина находится в точке B, а два луча проходят через точки A и C.

Какие бывают виды углов?

В математике существует несколько видов углов. Острый угол имеет меньшую меру 90 градусов, прямой угол равен 90 градусам, тупой угол больше 90 градусов, а полный угол равен 180 градусам. Также существуют отрицательные углы, которые имеют меру больше 180 градусов, и внутренние и внешние углы в многоугольниках.

Как измеряются углы в математике?

Углы могут быть измерены в градусах, радианах или градусно-минутно-секундных делениях. Градус — это наиболее распространенная единица измерения углов. Один полный оборот равен 360 градусам. Радиан — это другая единица измерения углов, которая основана на радиусе окружности. Один полный оборот равен 2π радианам. Градусно-минутно-секундные деления используются для более точного измерения углов.

Можно ли привести примеры углов в повседневной жизни?

Да, конечно! Углы встречаются повсюду в нашей повседневной жизни. Например, углы между стенами в комнате, углы на строительных чертежах, углы в колесе автомобиля, углы при открытии двери, углы между линиями на дороге и многие другие. Углы имеют важное значение в архитектуре, инженерии, физике, астрономии и других областях.

Что такое угол?

Угол — это геометрическая фигура, образованная двумя лучами, исходящими из одной точки, которая называется вершиной угла. Угол может быть острый, прямой, тупой или полный в зависимости от своей величины. Угол измеряется в градусах и обозначается символом °.

Как обозначают углы в математике?

Углы в математике обозначаются буквами. Например, угол может быть обозначен буквами А, В, С и т.д. Буква, обозначающая угол, обычно ставится между вершиной и одним из лучей угла. Например, ABC — угол, где B — вершина, A и C — лучи угла.

Обозначение углов на плоскости

В математике углы обозначаются с помощью специальных символов и обозначений. Обозначение углов на плоскости позволяет удобно и однозначно указывать их размеры и положение.

Углы часто обозначаются с помощью трех букв, указывающих вершины угла. Например, угол ABC образован лучами AB и BC, и его вершина находится в точке B.

Если требуется указать только один угол, то используют одну букву в верхнем индексе. Например, угол A обозначается как ∠A.

Иногда углы обозначаются с помощью точек и знака градуса. Например, угол ABC может быть обозначен как ∠ABC, а его значение — 60°.

Для обозначения прямого угла вместо буквы используется символ квадратного прямоугольника. Например, прямой угол обозначается как ∠.

В некоторых случаях, когда требуется указать, что два угла равны, используется символ равенства ( ≅ ). Например, если угол ABC равен углу DEF, то это можно записать как ∠ABC ≅ ∠DEF.

Обозначение углов на плоскости упрощает работу с геометрическими фигурами и позволяет точно указывать их свойства и отношения.

Обозначение углов в пространстве

Обозначение углов в пространстве осуществляется с помощью специальных символов. Один из самых распространенных способов обозначения углов – использование трех букв. Каждая буква обозначает вершину угла, а символ «^» указывает нас на направление от первой буквы ко второй и третьей.

Например, угол ABC обозначает угол, в котором вершина находится в точке B, луч AB направлен к точке A, а луч BC – к точке C.

Другим способом обозначения углов является использование индексов. Угол ABC, где B – вершина, A – первая точка на луче AB, C – вторая точка на луче BC, может быть обозначен как угол ∠BAC или ∠CAB.

Также углы могут быть обозначены с помощью греческих букв. Например, ∠α, ∠β, ∠γ. В этом случае буква обозначает вершину угла, а символ ∠ указывает нас на то, что это угол.

Правильное обозначение углов в пространстве позволяет удобно описывать геометрические фигуры и проводить вычисления с углами. Знание основных способов обозначения углов позволяет более точно и ясно передать информацию о геометрической фигуре или задаче, связанной с углами.

Примеры углов в геометрии

Острый угол: острый угол имеет величину меньше 90 градусов. Примером острого угла может быть угол внутри прямоугольного треугольника.

Тупой угол: тупой угол имеет величину больше 90 градусов, но меньше 180 градусов. Примером тупого угла может быть угол внутри тупоугольного треугольника.

Полный угол: полный угол имеет величину 180 градусов и составляет полный оборот. Он образуется двумя противоположными линиями, которые пересекаются.

Примеры углов в повседневной жизни

1. Углы на часах

На циферблате часов мы видим различные углы. Например, угол между стрелками часов и минутной стрелкой меняется каждую минуту.

2. Углы в строительстве

При строительстве зданий и сооружений используются различные углы. Например, прямые углы используются для создания прямых стен, а острые углы могут использоваться для создания острых поверхностей или крыш.

3. Углы в дорожном движении

В дорожном движении мы сталкиваемся с углами каждый день. Например, углы поворота автомобиля при движении на перекрестках или углы наклона дороги при движении по горам.

4. Углы в спорте

Во многих видах спорта углы играют важную роль. Например, при игре в футбол угол между игроками и мячом определяет направление удара, а в гимнастике углы определяют гибкость и позы спортсменов.

5. Углы в искусстве и дизайне

В искусстве и дизайне углы используются для создания гармоничных композиций. Например, углы между линиями и фигурами определяют перспективу и композицию произведения искусства.

В повседневной жизни мы постоянно взаимодействуем с углами и часто даже не задумываемся об их наличии. Они присутствуют во множестве ситуаций и помогают нам понять и описать окружающий мир.

Важность знания обозначения углов

Правильное обозначение углов также помогает избежать путаницы и ошибок при решении задач. Когда каждый угол имеет свое уникальное обозначение, нет места для неоднозначности или непонимания. Это особенно важно при решении сложных заданий или доказательств, где даже небольшая ошибка может привести к неправильному результату.

Знание обозначения углов также полезно в повседневной жизни. Например, при строительстве или ремонте дома важно понимать обозначение углов для правильного измерения и расчетов. Это помогает сделать работу более точной и эффективной.

Кроме того, знание обозначения углов помогает развивать логическое мышление и абстрактное мышление. Понимание, как обозначать и работать с углами, помогает развивать навыки анализа и решения проблем, которые могут быть применимы в различных областях жизни.

В целом, знание обозначения углов является важным инструментом для понимания и работы с геометрическими фигурами и концепциями. Оно помогает ученым, студентам и людям в повседневной жизни делать точные вычисления, измерения и прогнозировать результаты. Поэтому понимание обозначения углов является необходимым навыком для достижения успеха в математике и других областях.