Что такое угол по математике

Угол в математике — это геометрическая фигура, образованная двумя полупрямыми, которые имеют общую точку начала. Углы измеряются в градусах и используются для изучения геометрии и решения различных задач. Узнайте, что такое угол и как его измерять в математике.

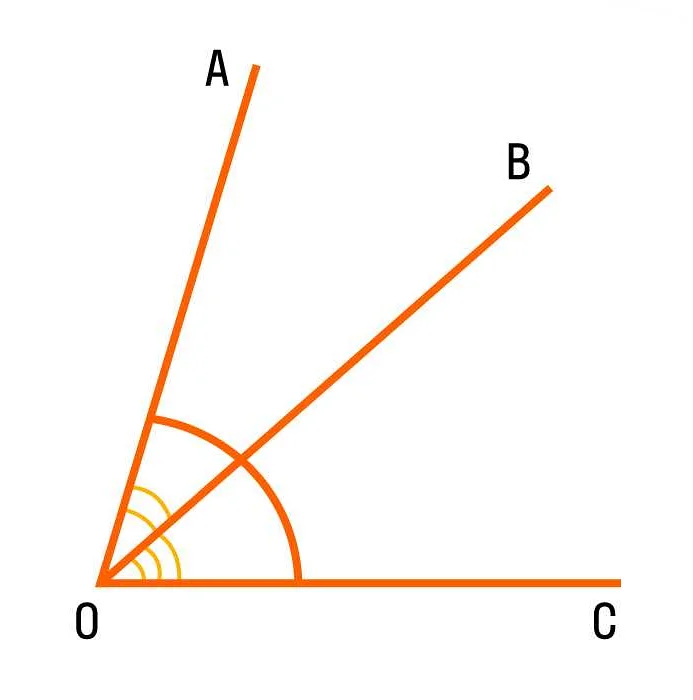
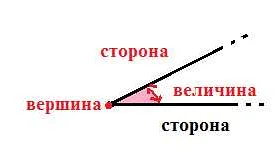
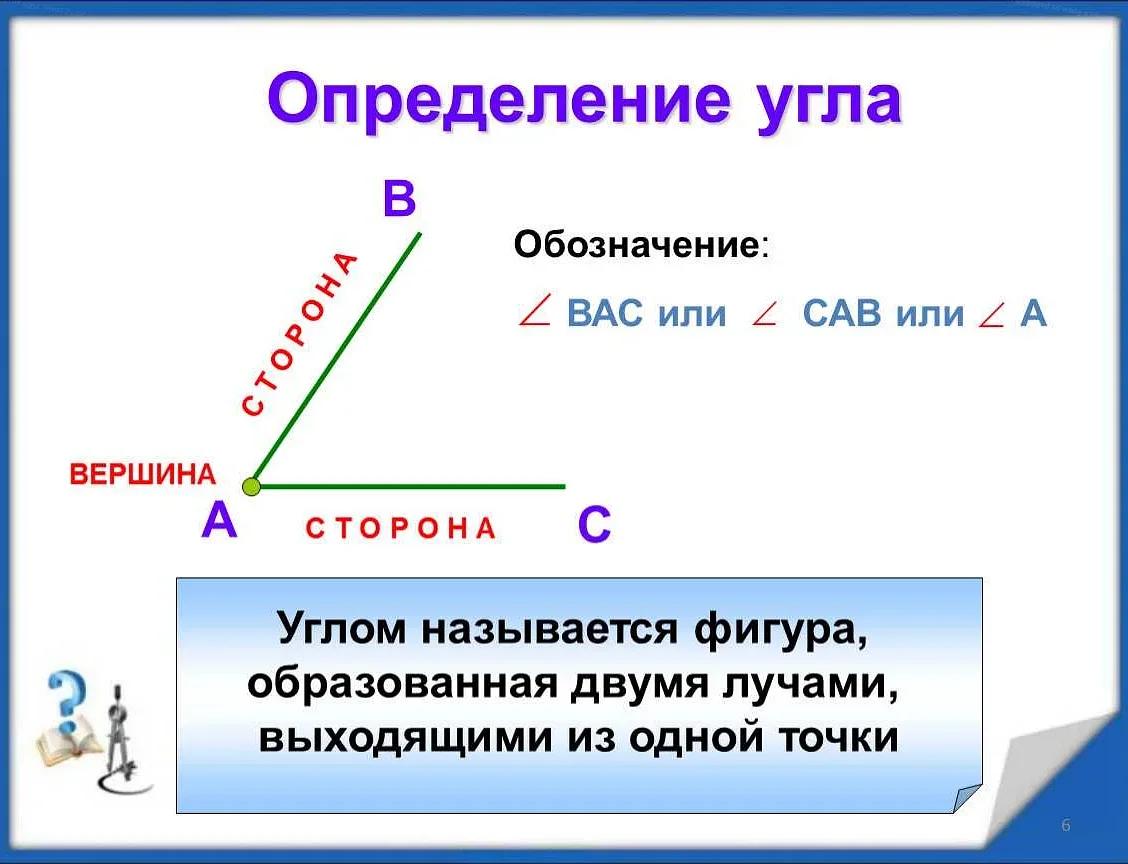
Угол — это геометрическая фигура, образованная двумя лучами, имеющими общее начало. В математике углы являются одной из основных составляющих геометрии и широко используются в различных областях науки и техники. Они позволяют изучать и описывать различные пространственные и плоские объекты, а также решать задачи из геометрии, физики, астрономии и других наук.

Углы могут быть разных видов, в зависимости от их величины и взаимного положения лучей. Наиболее распространенные виды углов — прямой угол, острый угол и тупой угол. Прямой угол — это угол, который равен 90 градусам и образуется двумя перпендикулярными лучами. Острый угол — это угол, который меньше 90 градусов. Тупой угол — это угол, который больше 90 градусов, но меньше 180 градусов.

Основные свойства углов позволяют проводить различные операции с ними. Например, сумма всех углов в треугольнике равна 180 градусам. Если два угла смежны и образуют прямой угол, то эти углы называются смежными прямыми углами и равны между собой. Углы, которые имеют общую вершину и общую сторону, называются смежными углами. Смежные углы дополняющие, если их сумма равна 180 градусам.

Смысл и определение угла

Определение угла основано на понятии поворота. Угол измеряется в градусах, минутах и секундах. Один градус составляет 1/360 полного поворота, а одна минута и одна секунда составляют соответственно 1/60 и 1/3600 градуса.

Угол можно представить с помощью геометрической фигуры, называемой полукругом. Полукруг делится на 180 равных долей, которые соответствуют градусам. Таким образом, угол можно измерять, сравнивая его с этими долями полукруга.

Виды угловОписание

Острый угол	Угол, который меньше 90 градусов.
Прямой угол	Угол, который равен 90 градусов.
Тупой угол	Угол, который больше 90 градусов и меньше 180 градусов.
Развернутый угол	Угол, который равен 180 градусов.

Углы могут быть измерены с помощью геометрических инструментов, таких как гониометр или транспортир. Они также могут быть выражены символически с использованием специальных обозначений и формул.

Видео по теме:

Виды углов

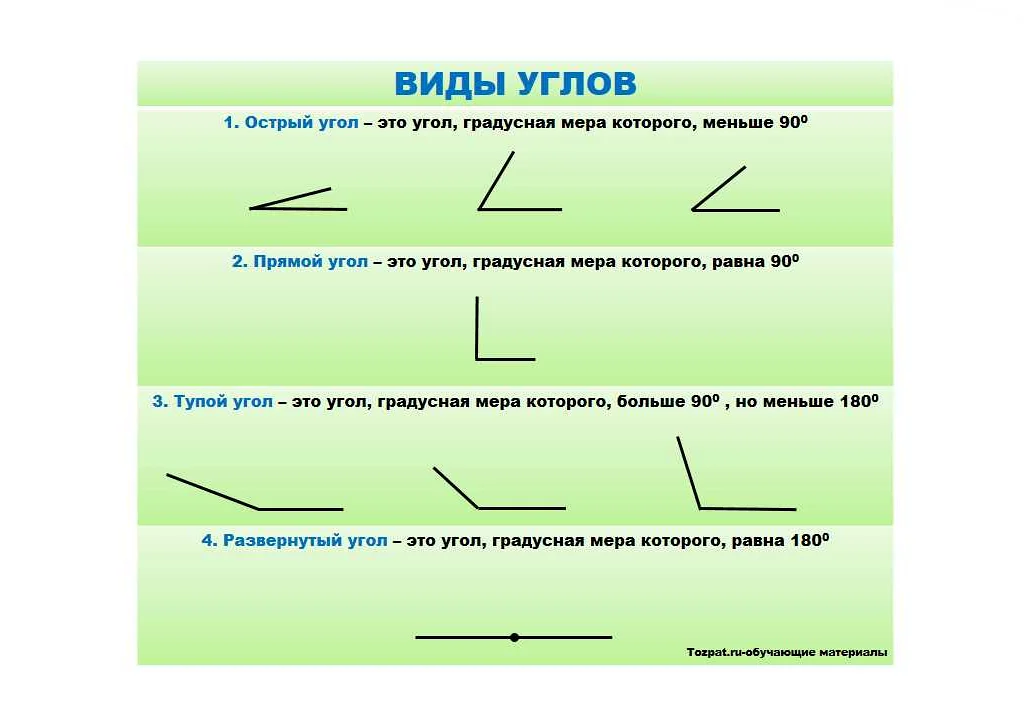
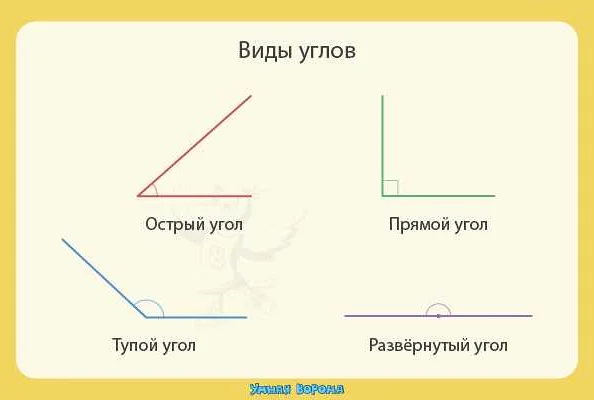
В математике существуют различные виды углов, которые классифицируются в зависимости от своего размера и положения. Ниже приведены основные виды углов:

1. Прямой угол. Прямой угол равен 90 градусам и образуется двумя перпендикулярными лучами. Прямой угол является одним из наиболее распространенных и простых видов углов.

2. Острый угол. Острый угол меньше 90 градусов и образуется двумя лучами, которые встречаются в точке и направлены внутрь угла. Острый угол имеет форму острия и широко используется в геометрии.

3. Тупой угол. Тупой угол больше 90 градусов и образуется двумя лучами, которые встречаются в точке и направлены наружу угла. Тупой угол имеет форму заостренного угла и также используется в геометрии.

4. Равный угол. Равный угол имеет размер 180 градусов и образуется двумя лучами, которые встречаются в точке и лежат на одной прямой. Он также называется прямой угол, так как формирует прямую линию.

5. Разносторонний угол. Разносторонний угол имеет все стороны различной длины и все углы различной величины. Этот вид угла может быть любого размера и формы.

Это лишь некоторые из видов углов, которые встречаются в математике. Каждый вид угла имеет свои уникальные свойства и применение в различных областях науки и техники.

Основные свойства углов

1. Сумма углов в треугольнике. Сумма всех углов внутри треугольника равна 180 градусам. Это свойство позволяет вычислять один из углов, зная значения двух других.
2. Свойство вертикальных углов. Вертикальные углы, образованные пересекающимися прямыми, равны между собой. Это свойство позволяет находить значения одного угла, зная значение другого, и использовать их для решения геометрических задач.
3. Свойство смежных углов. Смежные углы, образованные пересекающимися прямыми, дополнительны. То есть, их сумма равна 180 градусам. Это свойство позволяет вычислять значение одного угла, зная значение другого, и использовать их для решения задач на геометрическую подобность.
4. Свойство перпендикулярных углов. Перпендикулярные углы, образованные пересекающимися прямыми, равны между собой. Это свойство используется при доказательстве теорем о параллельности прямых.
5. Свойство комплементарных углов. Комплементарные углы, сумма которых равна 90 градусам, являются дополнительными. Это свойство используется для решения задач на нахождение неизвестных углов.

Углы являются важным понятием в геометрии и находят применение в различных областях, таких как строительство, архитектура, физика и многие другие.

Вопрос-ответ:

Что такое угол в математике?

Угол в математике — это фигура, образованная двумя лучами с общим началом. Один из лучей называется начальной стороной, другой — конечной. Угол измеряется в градусах.

Какие бывают виды углов?

В математике существуют различные виды углов. Они могут быть прямыми, острыми, тупыми, полными, нулевыми и отрицательными. Прямой угол равен 90 градусам, острый — меньше 90 градусов, тупой — больше 90 градусов, полный — равен 180 градусам, нулевой — это отсутствие угла, а отрицательный угол — это угол, который направлен в противоположную сторону.

Какие свойства имеют углы?

Углы обладают различными свойствами. Например, сумма углов треугольника равна 180 градусам. В прямоугольном треугольнике сумма двух острых углов равна 90 градусам. Вертикальные углы равны друг другу. Также существуют формулы для вычисления значений смежных и дополнительных углов.

Как измерять углы?

Углы измеряются в градусах. Существуют также другие системы измерения углов, такие как радианы и грады, но градусы являются наиболее распространенным и понятным способом измерения угла.

Какие примеры применения углов в реальной жизни?

Углы имеют множество применений в реальной жизни. Например, они используются в архитектуре для построения зданий и мостов. Углы также применяются в навигации для определения направления. Они используются в физике для описания движения и сил. В геометрии углы играют важную роль при решении задач на нахождение периметра, площади и объема фигур.

Острый угол и его характеристики

1. Размер: Острый угол всегда меньше 90 градусов. Он может быть как большой, так и маленький, но его размер всегда будет меньше прямого угла.

2. Расположение: Острый угол может быть расположен в разных частях плоскости. Он может быть вертикальным, горизонтальным или наклонным. В зависимости от своего расположения, острый угол может иметь различные формы.

3. Смежность: Острый угол может быть смежным с другими углами. Смежные острые углы имеют общую сторону и вершину.

4. Сумма: Сумма двух острых углов всегда будет меньше 180 градусов. Например, если один острый угол равен 60 градусов, то второй острый угол не может быть больше 120 градусов.

5. Измерение: Острый угол измеряется в градусах. Обычно используется градусная мера, но также можно использовать и другие единицы измерения, такие как радианы или грады.

Острый угол является основным понятием в геометрии и играет важную роль в решении различных задач. Понимание основных характеристик острого угла позволяет лучше понять его свойства и использовать их в практических задачах.

Тупой угол и его особенности

Основными особенностями тупого угла являются:

1. В тупом угле одна из его сторон является продолжением другой стороны.
2. Сумма тупого угла и острого угла составляет 180 градусов – полный угол.
3. Тупой угол может быть образован при пересечении двух отрезков или при повороте одного отрезка относительно другого.
4. Угол между двумя лучами или отрезками, принадлежащими одной прямой, не может быть тупым.

Тупые углы встречаются в различных геометрических фигурах и конструкциях. Зная их особенности, можно легче анализировать и решать геометрические задачи, связанные с такими углами.

Прямой угол и его значение

Значение прямого угла заключается в его свойствах и возможностях использования в различных областях. Он часто используется в геометрии, физике и других науках для измерения и описания углов и направлений.

Прямой угол образуется двумя перпендикулярными линиями, которые пересекаются в точке. Он также может быть определен как половина прямого угла или две прямых стороны линейного угла.

Прямой угол имеет несколько важных свойств. Он является самым большим углом, который может быть образован в плоскости, и является идеальным углом для создания перпендикулярных линий и прямоугольных форм.

Свойства прямого угла:Значение:

Величина угла:	90 градусов
Сумма углов вокруг точки:	360 градусов
Перпендикулярные линии:	Образуют прямой угол
Прямоугольные формы:	Имеют четыре прямых угла

Прямой угол играет важную роль в различных областях науки и практического применения. Он используется при построении зданий, дизайне интерьеров, изучении геометрии и других математических дисциплин, а также в физике, навигации и многих других областях.

Расположение углов относительно друг друга

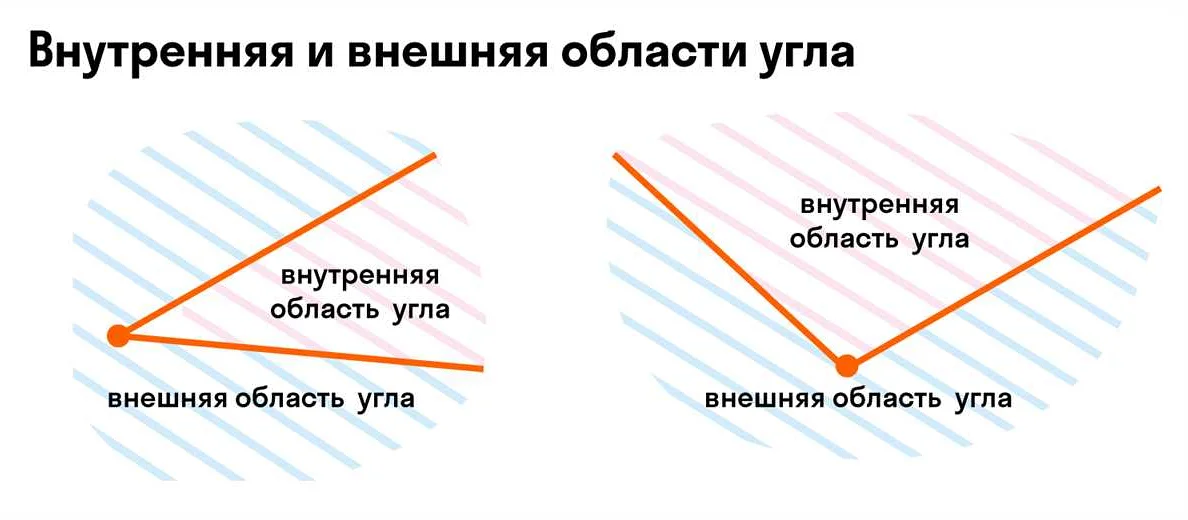
В математике углы могут располагаться относительно друг друга по разным правилам и свойствам. Знание этих особенностей позволяет более точно и удобно работать с углами и решать задачи связанные с ними.

Основные виды расположения углов:

• Смежные углы — углы, имеющие общую сторону и общую вершину, но не перекрывающиеся;
• Вертикальные углы — пары углов, противоположные друг другу и расположенные по разные стороны пересекающихся прямых. Вертикальные углы имеют одинаковую величину;
• Суплементарные углы — два угла, сумма которых равна 180°;
• Комплементарные углы — два угла, сумма которых равна 90°;
• Прямые углы — углы, сумма которых равна 180°;
• Острый угол — угол, меньше 90°;
• Тупой угол — угол, больше 90°, но меньше 180°;
• Полный угол — угол, равный 180°;
• Рефлексивный угол — угол, больше 180°, но меньше 360°;
• Контррефлексивный угол — угол, больше 360°.

Знание и понимание основных свойств и расположения углов позволяет более эффективно работать с ними и применять в решении задач различной сложности.

Примеры применения углов в реальной жизни

• В архитектуре углы используются для создания и проектирования зданий. Архитекторы используют углы для определения формы и структуры здания, а также для расчета необходимых материалов.
• В географии углы используются для измерения направления и поворотов на карте. Например, при использовании компаса для определения магнитного направления.
• В авиации углы используются для навигации и управления самолетами. Пилоты используют углы для определения курса, угла подъема и поворотов.
• В строительстве углы используются для создания прямых и закругленных структур. Углы также используются для определения плоскостей и уровней.
• В машиностроении углы используются для проектирования и изготовления деталей и механизмов. Углы помогают определить точное положение и ориентацию деталей.
• В физике углы используются для измерения и анализа движения и сил. Углы помогают понять законы движения тел и взаимодействие силы с объектами.
• В спорте углы используются для определения траектории и силы удара. Например, в гольфе углы помогают выбрать правильный удар для достижения цели.

Это лишь некоторые примеры использования углов в реальной жизни. Углы широко применяются в различных областях нашей повседневной жизни и являются важным инструментом для понимания и описания мира вокруг нас.