Угол что это такое в математике
Содержимое
- 1 Угол что это такое в математике
Угол в математике — это геометрическая фигура, образованная двумя лучами, исходящими из одной точки. Угол определяется его величиной, измеряемой в градусах, минутах или радианах, а также его типом, таким как прямой, острый или тупой угол. Углы широко используются в геометрии, физике и других науках, а также в повседневной жизни для измерения и описания направления и поворотов.
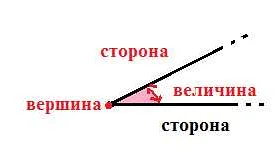
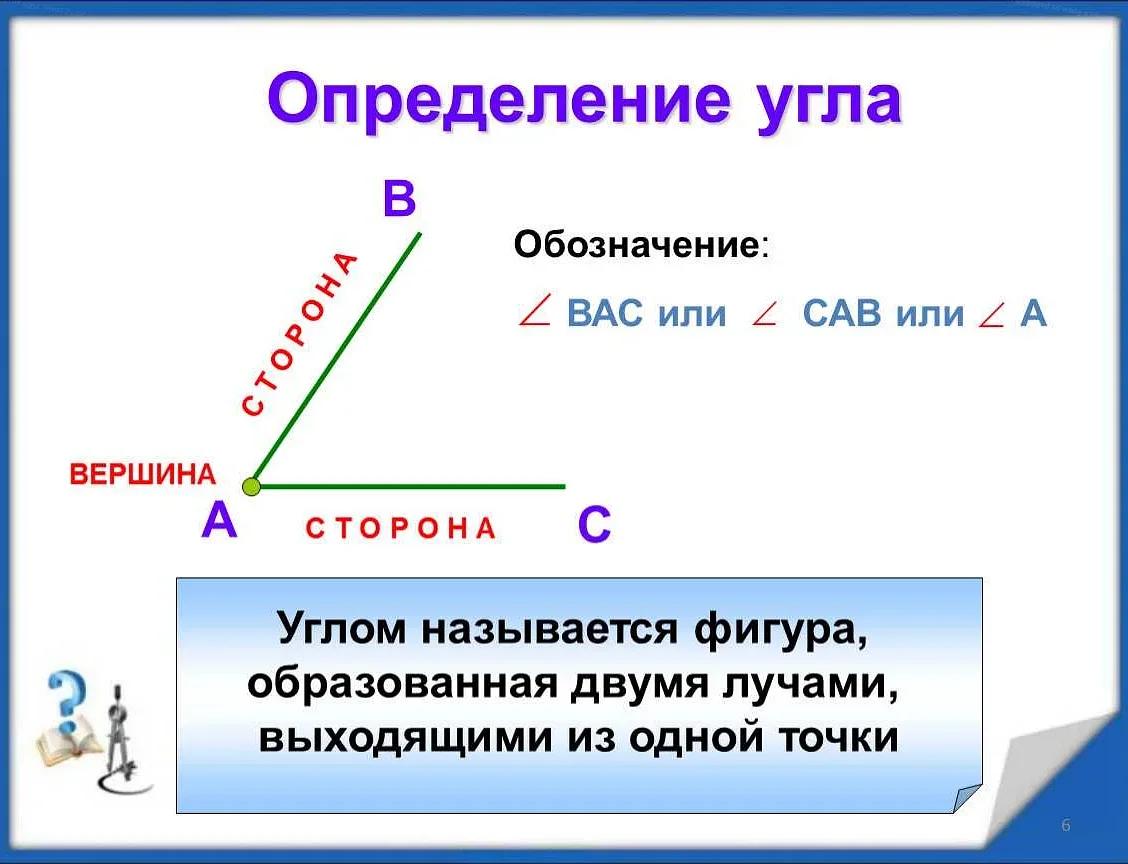
Угол — это геометрическая фигура, образованная двумя лучами, исходящими из одной точки, которая называется вершиной угла. В математике угол является одним из основных понятий и широко используется при изучении геометрии и тригонометрии.
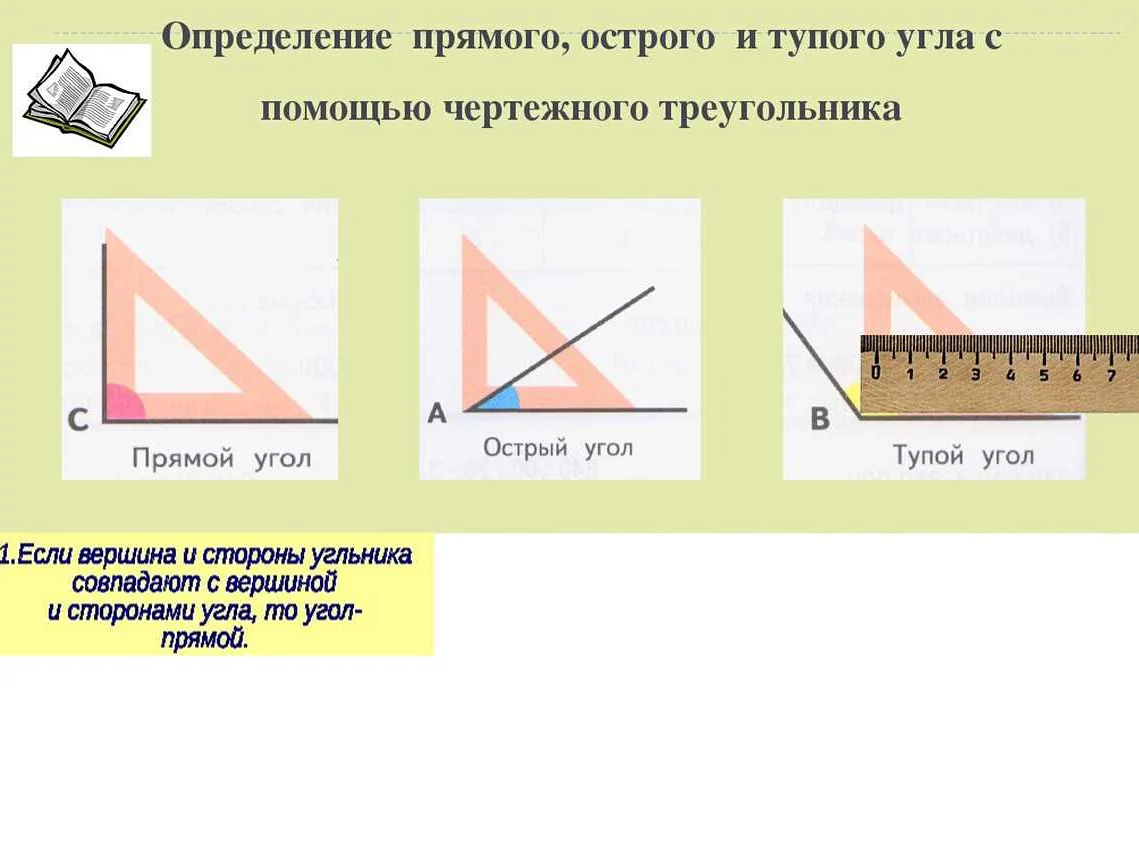
Углы могут иметь различные виды, в зависимости от взаимного расположения лучей и положения вершины. Основными видами углов являются прямой угол, острый угол, тупой угол и полный угол. Прямой угол равен 90 градусам и образуется двумя перпендикулярными лучами. Острый угол меньше 90 градусов, тупой угол больше 90 градусов, а полный угол равен 360 градусам.
Углы обладают рядом основных свойств, которые являются основой для решения задач и построения геометрических конструкций. Например, сумма всех углов треугольника равна 180 градусов. Углы, дополнительные друг к другу, в сумме дают прямой угол. Углы, смежные друг к другу, образуют линейные пары, сумма которых равна 180 градусов.
Понимание основных понятий и свойств углов является важным фундаментом для успешного изучения геометрии и тригонометрии. Знание углов позволяет решать задачи, строить фигуры и делает понимание пространства более углубленным.
Понятие угла в математике
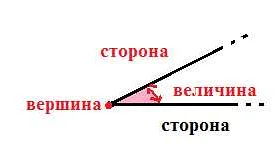
Углы могут быть различных видов в зависимости от их величины. Величина угла измеряется в градусах (°), минутах (′) и секундах (″). Один градус делится на 60 минут, а одна минута – на 60 секунд.
Углы можно классифицировать по их величине:
- Острый угол: угол с величиной меньше 90°.
- Прямой угол: угол с величиной 90°.
- Тупой угол: угол с величиной больше 90° и меньше 180°.
- Полный угол: угол с величиной 180°.
Углы также могут быть смежными, вертикальными или суплементарными в зависимости от их взаимного расположения и свойств.
Видео по теме:
Угол как геометрическая фигура
Углы могут быть различных видов в зависимости от их величины и положения. Величина угла измеряется в градусах, минутах и секундах. Существуют следующие виды углов:
Вид углаОписание
| Острый угол | Угол, величина которого меньше 90 градусов. |
| Прямой угол | Угол, величина которого равна 90 градусов. |
| Тупой угол | Угол, величина которого больше 90 градусов, но меньше 180 градусов. |
| Полный угол | Угол, величина которого равна 180 градусов. |
Углы в математике имеют ряд основных свойств и правил, которые позволяют решать различные задачи. Например, сумма углов треугольника равна 180 градусов, а сумма углов вокруг точки равна 360 градусов.
Изучение углов позволяет решать задачи связанные с геометрией, тригонометрией, а также применять их в практических задачах, например, в архитектуре и инженерии.
Размеры углов и их измерение
Для измерения углов используются различные единицы измерения. Одной из наиболее распространенных является градус (°). Градус представляет собой 1/360 часть целого угла, который равен полному обороту.
Для углов, меньших чем градус, используются минуты (‘), которые представляют 1/60 часть градуса, и секунды («), которые представляют 1/60 часть минуты. Таким образом, 1 градус равен 60 минутам или 3600 секундам.
Также существуют другие системы измерения углов, такие как радианы и гони. Радиан является более естественной единицей измерения угла и определяется как отношение длины дуги окружности к радиусу. Гонь представляет собой 1/400 часть полного угла.
Измерение углов позволяет проводить различные геометрические операции, такие как сумма углов, построение треугольников и многоугольников, а также решение задач на геометрических фигурах.
Вопрос-ответ:
Что такое угол в математике?
Угол в математике — это фигура, образованная двумя лучами, которые имеют общее начало, называемое вершиной угла.
Сколько видов углов существует?
В математике существует несколько видов углов: острые, прямые, тупые, ровные, вписанные, внешние и другие.
Как определить вид угла?
Вид угла определяется по его величине. Острый угол имеет размер меньше 90 градусов, прямой — равный 90 градусов, а тупой — больше 90 градусов.
Какие свойства имеют углы?
Углы имеют ряд свойств, таких как сумма углов треугольника равна 180 градусов, смежные углы дополнительны, вертикальные углы равны друг другу и много других.
Зачем нужны углы в математике?
Углы играют важную роль в геометрии и физике. Они используются для измерения и описания форм и движений объектов, а также в решении различных математических задач.
Что такое угол в математике?
Угол в математике — это геометрическая фигура, образованная двумя лучами, начало которых совпадает в одной точке. Угол измеряется в градусах и может иметь различные значения, от 0 до 360 градусов.
Какие виды углов существуют?
В математике существует несколько видов углов. Одним из самых распространенных видов является прямой угол, который равен 90 градусам. Также существуют острые углы, которые меньше 90 градусов, и тупые углы, которые больше 90 градусов. Существуют также полные углы, которые равны 360 градусам, и нулевой угол, который равен 0 градусам.
Основные виды углов
В математике существует несколько основных видов углов, которые имеют свои особенности и характеристики:
Прямой угол: это угол, который равен 90 градусам. В прямом угле стороны лежат на одной прямой и образуют прямую линию.
Острый угол: это угол, который меньше прямого угла и составляет менее 90 градусов. Острый угол имеет острые вершины и заостренные стороны.
Тупой угол: это угол, который больше прямого угла и составляет более 90 градусов. Тупой угол имеет тупую вершину и заогнутые стороны.
Смежные углы: это углы, у которых одна сторона общая и лежит на одной прямой. Сумма смежных углов равна 180 градусам.
Вертикальные углы: это углы, у которых стороны являются продолжением друг друга и пересекаются в одной точке. Вертикальные углы равны между собой.
Сопряженные углы: это углы, у которых стороны являются продолжением друг друга и пересекаются в одной точке. Сумма сопряженных углов равна 180 градусам.
Дополнительные углы: это пара углов, сумма которых равна 180 градусам. В дополнительных углах один угол является дополнением другого.
Смежно-дополнительные углы: это пара углов, один из которых является смежным, а другой дополнительным. Смежно-дополнительные углы в сумме равны 180 градусам.
Изучение и понимание основных видов углов позволяет более глубоко разобраться в геометрии и решать различные задачи, связанные с углами и их свойствами.
Острые углы и их свойства
Острые углы обладают следующими свойствами:
- Сумма двух острых углов всегда составляет меньше 180 градусов. То есть острые углы не могут образовывать прямую или тупую сумму.
- Острый угол может быть равен другому острым углам.
- Острый угол может быть вписанным в окружность, при этом его вершина будет находиться на окружности, а стороны угла будут лежать на линиях, соединяющих вершину с различными точками окружности.
- Острый угол может быть острым треугольником, где все три его угла являются острыми углами.
- В остром треугольнике, наибольшая сторона всегда противолежит наибольшему углу, а наименьшая сторона — наименьшему углу.
Острые углы играют важную роль в геометрии и находят применение в различных областях науки и техники. Изучение их свойств и взаимосвязей с другими фигурами помогает строить сложные геометрические модели и решать разнообразные задачи.
Прямой угол и его характеристики
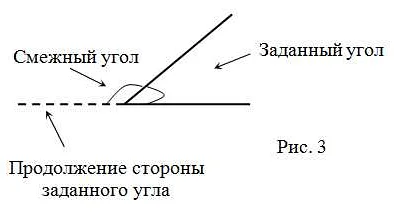
Основные характеристики прямого угла:
- Все его стороны равны между собой.
- Сумма его двух угловых сторон равна 180 градусов.
- Он может быть образован пересечением двух перпендикулярных линий или отрезков.
Прямой угол является одним из основных видов углов и обладает множеством свойств и применений в геометрии и других науках.
Тупые углы и их особенности
| Определение | Тупой угол — это угол, у которого внутренняя мера больше 90 градусов и меньше 180 градусов. |
| Вид | Тупые углы бывают разных видов в зависимости от их меры. Например, угол в 100 градусов и угол в 170 градусов оба являются тупыми углами. |
| Изображение | Тупой угол обычно обозначается соответствующим символом — «∠» с острым углом внутри. Например, ∠ABC, где угол BAC является тупым углом. |
| Свойства | Тупой угол является отражением противоположного острого угла относительно прямой. Например, если у нас есть острый угол в 60 градусов, то его тупой дополнительный угол будет составлять 120 градусов. |
Таким образом, тупые углы имеют свои особенности, которые позволяют определить их вид и рассчитать их меру в градусах. Они являются важной частью геометрии и находят применение в различных областях науки и техники.
Смежные и вертикальные углы
Вертикальные углы — это пара углов, которые имеют общую вершину, а противоположные стороны являются продолжениями друг друга. Вертикальные углы равны между собой, то есть имеют одинаковую меру.
Смежные и вертикальные углы являются важными понятиями в геометрии. Они помогают нам анализировать и разбираться в различных угловых отношениях.



В статье очень интересно описаны углы в математике. Я всегда задумывался, что такое угол и какие бывают его виды. Статья подробно раскрывает эту тему, объясняя определение угла и его основные свойства. Мне особенно понравилось, что автор привел примеры разных видов углов, таких как острый, прямой и тупой. Было интересно узнать, что сумма углов в треугольнике всегда равна 180 градусам. Теперь я лучше понимаю, как работает геометрия и как применять знания об углах в повседневной жизни. Спасибо за полезную информацию!
Статья очень понравилась! Я всегда интересовалась математикой, и угол — одна из самых захватывающих тем. Статья содержит полное и понятное определение угла, которое даже новичок в математике сможет понять. Мне понравилось, как автор рассказал о различных видах углов, таких как прямой, острый и тупой. Это помогло мне лучше понять, как они выглядят и как их измерять. Кроме того, статья также обсуждает основные свойства углов, как например, то что сумма углов в треугольнике равна 180 градусам. Это очень важная информация, которая помогает решать задачи на геометрию. В общем, статья была полезной и интересной, и я советую ее прочитать всем, кто хочет узнать больше о углах и их свойствах.