Обратная задача в математике: что это такое и как ее решают?

Обратная задача в математике — это задача, при которой необходимо найти входные данные на основе известных выходных данных. Она применяется в разных областях науки и техники, включая физику, экономику, медицину, компьютерную графику и другие. В статье объясняются основы обратной задачи и примеры ее применения.

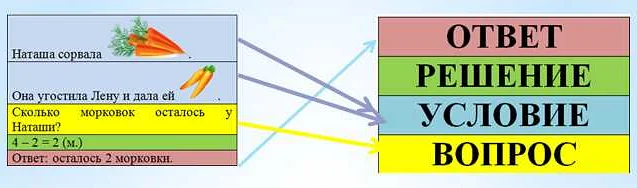
Математика – это наука о числах, формулах и принципах решения. Среди большого количества математических задач есть такая, которая называется обратной. Она отличается от классической тем, что ее решение заключается не в восстановлении ответа на задачу, а в определении исходных данных, чтобы получить желаемый результат.

Обратная задача является фундаментальным принципом в промышленности, науке и медицине, так как позволяет предсказать и контролировать результаты различных систем, например, химических реакций, движения частиц в жидкостях и газах, процессов искусственного интеллекта и других. В этой статье мы рассмотрим основы решения обратной задачи в математике.

Сложность задачи заключается в том, что исходные данные, которые нужно найти, скрыты или неполные. Иногда даже неизвестно, какие данные нужны для получения ответа. Однако, с помощью уравнений и алгоритмов можно вычислить параметры системы, которые нужно искать. Решение обратной задачи требует знаний и опыта в выборе и описании математических моделей для достижения желаемого результата.

Обратная задача в математике: принципы решения

Обратная задача в математике – это задача, которая заключается в восстановлении исходных данных по результатам экспериментов или измерений. Применяется она в различных областях науки, таких как физика, химия, биология, медицина, геология и т.д. Важнейшим принципом решения обратной задачи является использование метода обратного оператора.

Метод обратного оператора заключается в том, что исходные данные восстанавливаются путем обращения оператора наблюдения. Этот метод используется во многих областях науки, в том числе в задачах медицинской диагностики, астрономии, физике и т.д.

Важным принципом решения обратной задачи является точность использованных моделей. Модель описывает математические связи между исходными данными и результатами измерений. Если модель не точна, то результаты могут быть неточными. В начале задачи необходимо придумать модель, затем провести измерения и, наконец, построить обратную модель.

Таким образом, для решения обратной задачи в математике необходимо применять соответствующие методы и обращать внимание на точность используемых моделей. Важно также учитывать погрешности измерений и уточнения моделей на основе новых данных.

Видео по теме:

Что такое обратная задача в математике?

Обратная задача в математике — это задача, в которой требуется найти параметры математической модели, отвечающие данным, полученным в результате эксперимента или наблюдения в реальном мире. Это означает, что вместо того, чтобы вычислять результаты на основе значений параметров, мы ищем значения параметров, чтобы получить заданный набор результатов.

Обратные задачи широко используются в науке и инженерии, где они помогают в оценке неизвестных параметров системы на основе ее поведения или результатов тестирования. Например, задача определения характеристик материала по результатам испытаний является обратной задачей.

Решение обратных задач часто основано на методах оптимизации или статистической обработки данных, включая многомерный анализ, аппроксимацию функций, регрессионный анализ и другие статистические методы. В целом, обратные задачи в математике постоянно развиваются и находят все новые приложения в различных областях науки и технологий.

Зачем нужно решать обратные задачи?

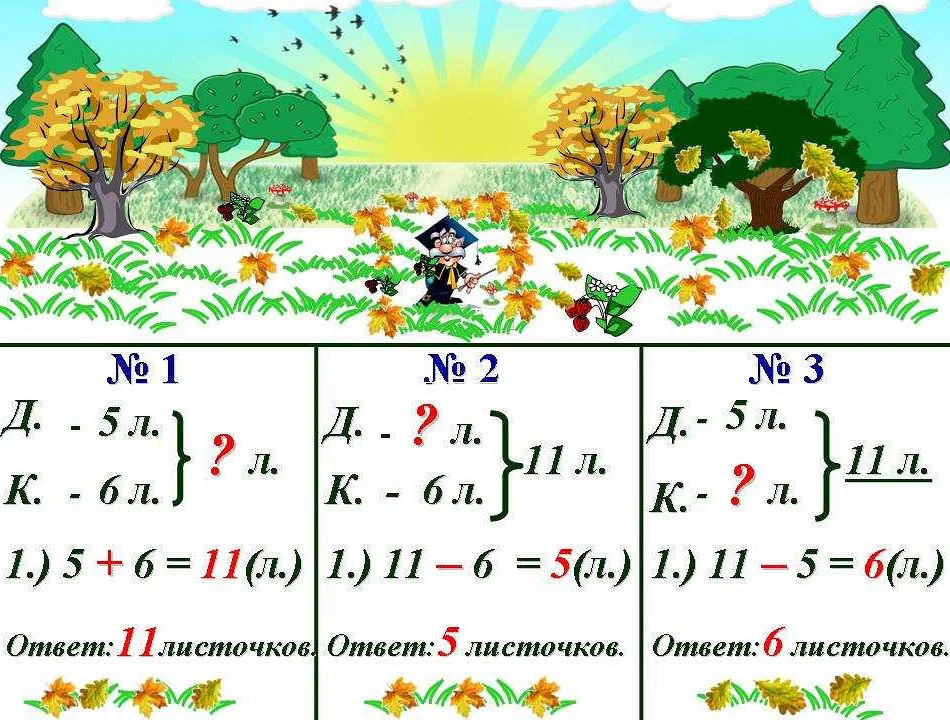
Обратные задачи в математике встречаются очень часто. Они заключаются в том, чтобы, зная ответ на вопрос, найти параметры, которые привели к этому ответу. Если необходимость решить прямую задачу в математике встречается ежедневно, то обратные задачи служат для вычислений и в науке, и в технике, и в физике, и в медицине, и в экономике.

Обратные задачи позволяют уточнить, привести к конфигурации, исправить или разработать новые технологии, новые материалы. В экономике обратные задачи часто используются для принятия решений, в медицине- для выявления и изучения заболеваний, в геологии и астрономии — для изучения и предсказания природных катаклизмов.

В целом, решение обратных задач имеет большое значение в нашей жизни и позволяет решать сложные задачи почти в любой области знаний. Для разработки новых технологий и изобретений, для анализа и определения опасных процессов и явлений — обратные задачи необходимы и не заменимы.

Вопрос-ответ:

Что такое обратная задача в математике?

Обратная задача — это задача, в которой требуется определить неизвестные параметры системы, исходя из наблюдаемых или известных входных и выходных данных.

Какие методы решения обратных задач существуют?

Существует множество методов решения обратных задач в зависимости от типа задачи и её сложности: методы аналитического решения, численные методы, методы оптимизации, методы машинного обучения, методы статистического анализа.

Какие области применения обратной задачи в математике?

Обратная задача используется во многих областях, таких как физика, механика, теплопередача, биология, медицина, экономика и т.д.

Как связаны прямая и обратная задачи?

Прямая задача определяет, как система будет действовать при заданных входных параметрах, а обратная задача определяет, какие входные параметры необходимо выбрать, чтобы получить желаемый результат.

Зачем нужна обратная задача в решении реальных проблем?

Решение обратной задачи позволяет определить неизвестные параметры системы, что может быть полезно в множестве сфер, например, при прогнозировании погоды, управлении финансовыми рынками, прогнозировании развития заболеваний и создании эффективных лекарств.

Какие сложности могут возникнуть при решении обратных задач?

Решение обратных задач может быть затруднено из-за недостатка входных данных, неоднозначности решения или избыточности информации. Также могут возникнуть проблемы со сходимостью численных методов.

Какие перспективы развития обратной задачи в математике?

Развитие обратной задачи становится всё более востребованным во многих научных областях и, вероятно, будет продолжаться в будущем. Улучшение методов решения обратных задач может привести к созданию новых технологий и приближению к решению некоторых важных научных и технических проблем.

Как выбрать подходящий метод решения?

Перед тем как выбрать метод решения обратной задачи, необходимо определить ее тип. Существуют различные категории обратных задач, такие как линейные или нелинейные, одномерные или многомерные, стационарные или нестационарные.

Для каждого типа обратной задачи существуют свои методы решения. Например, для линейных задач можно использовать методы МНК или Тихонова. Для нелинейных задач можно применять методы оптимизации, например, метод Ньютона или метод градиентного спуска. Для одномерных задач можно использовать дискретное преобразование Фурье, а для многомерных задач – методы преобразования волнового фронта или сеточные методы.

Выбор подходящего метода решения также зависит от размера выборки данных и сложности задачи. Для задач с большим количеством данных необходимо использовать методы оптимизации с различными видами регуляризации, чтобы избежать переобучения.

Важно также учитывать время вычислений и доступность соответствующего программного обеспечения для решения задачи. Не всегда самый эффективный метод будет подходящим решением в конкретной ситуации.

• Следует запомнить:
• — тип обратной задачи определяет доступные методы решения;
• — подбор конкретного метода зависит от размера выборки данных, сложности задачи и времени вычислений;
• — не всегда самый эффективный метод является подходящим решением.

Регуляризация: что это такое и как применить в решении задачи?

Регуляризация — это техника, которая используется в математике для снижения эффекта переобучения модели. При использовании этой техники модель не будет идеально подгоняться под все данные, а будет учитывать только главные характеристики.

При выборе метода регуляризации нужно обратить внимание на тип данных, которые обрабатывает модель. Например, для обработки текстовых данных хорошо подходит L1-регуляризация, а для сверточных нейронных сетей — L2-регуляризация.

Важно понимать, что регуляризация — это компромисс между точностью и обобщаемостью модели. Слишком много регуляризации может привести к потере точности, а слишком мало — к переобучению.

В решении задачи регуляризацию можно применять путем добавления и регулирования регуляризационных параметров. Они могут быть оптимизированы при помощи метода градиентного спуска. Также можно использовать специальные библиотеки для машинного обучения, которые содержат готовые методы регуляризации.

1. L1-регуляризация — используется для получения разреженных моделей, где большинство параметров равны нулю;
2. L2-регуляризация — используется для локализации весовых коэффициентов и уменьшения их значений;
3. Dropout — случайное зануление некоторых элементов входных данных для снижения эффекта переобучения;

Таким образом, используя регуляризацию, можно получить более устойчивую модель, которая будет обобщать данные лучше, чем без нее.

Методы оптимизации: как они помогают решить обратную задачу?

Методы оптимизации – это математические алгоритмы, которые помогают найти минимум или максимум функции. Они широко применяются для решения обратных задач в математике, так как обратная задача, как правило, сводится к поиску наиболее вероятных значений для неизвестных параметров.

Существует множество различных методов оптимизации, каждый из которых имеет свои преимущества и недостатки. Например, метод градиентного спуска используется для нахождения минимума функции путем последовательного движения в направлении наискорейшего убывания градиента, тогда как метод наименьших квадратов используется для минимизации суммы квадратов отклонений между предсказанными значениями и фактическими значениями.

Использование методов оптимизации является необходимым при решении обратных задач, так как позволяет находить наилучшее приближение к искомым значениям. Однако, необходимо учитывать, что выбор метода оптимизации должен быть основан на технических особенностях каждой конкретной задачи.

• Метод градиентного спуска;
• Метод наименьших квадратов;
• Метод Ньютона;
• Метод Монте-Карло;
• Метод Роя Главиков.

Таким образом, методы оптимизации являются важным инструментом при решении обратных задач в математике. Их правильный выбор может существенно повлиять на эффективность решения задачи и на достижение наилучшего результат.

Как выбрать оптимальное значение параметров в решении задачи?

При решении математических задач, в которых требуется выбрать оптимальное значение параметров, следует учитывать следующие факторы:

1. Понимание цели задачи:

Перед началом поиска оптимального значения параметров, необходимо понимать, какая цель стоит перед решением задачи. Например, если задача состоит в нахождении минимума функции, то необходимо выбирать такие значения параметров, при которых функция будет минимальной.

2. Анализ входных данных:

Перед выбором параметров следует проанализировать имеющиеся входные данные, чтобы понять их влияние на решение задачи. Например, если выбор определенного значения параметра существенно изменяет результат задачи, то необходимо уделить особое внимание этому параметру и подобрать его так, чтобы результат был оптимальным.

3. Использование методов оптимизации:

Существуют различные методы оптимизации, которые позволяют находить оптимальные значения параметров, такие как метод градиентного спуска, метод наискорейшего спуска и др. Их использование может помочь ускорить процесс поиска оптимальных значений параметров и улучшить результаты решения задачи.

4. Проверка результатов:

Важно проверять результаты решения задачи при использовании различных значений параметров. Это поможет выбрать оптимальные значения и убедиться в том, что они действительно являются оптимальными для данной задачи. Например, можно составить таблицу результатов для разных значений параметров и выбрать те значения, при которых результат был наилучшим.

Выбор оптимальных значений параметров при решении задач в математике является важным этапом, который требует тщательного анализа входных данных, использования методов оптимизации и проверки результатов. Однако, правильный выбор параметров позволяет получить наилучший результат и сделать решение задачи более эффективным.

Использование статистических методов в решении обратной задачи

Обратная задача заключается в определении исходных данных по результатам измерений. При решении этой задачи статистические методы являются эффективным инструментом для оценки оптимальных параметров модели, учета погрешностей и принятия решений на основе измерений.

Одним из наиболее распространенных методов является метод наименьших квадратов, который определяет параметры модели, минимизирующие сумму квадратов расхождений между измеренными и расчетными значениями. Этот метод может быть применен в различных областях, включая физику, инженерию, экономику и другие.

Другими статистическими методами, применяемыми при решении обратной задачи, являются методы максимального правдоподобия, байесовские методы и методы кластеризации. Метод максимального правдоподобия используется для определения параметров модели, наиболее вероятных для описания данных. Байесовские методы позволяют учитывать предыдущие знания при принятии решений, а методы кластеризации — выявлять характеристики отдельных групп данных.

Таким образом, применение статистических методов в решении обратной задачи позволяет получать более точные результаты при условии, что измерения проводятся с высокой точностью и учитываются все факторы, влияющие на результаты измерений.

Алгоритмы машинного обучения и обращение операторов

Алгоритмы машинного обучения — это методы анализа данных, при которых компьютер программируется для обучения на определенных данных и принятия решений в будущем. Один из важных аспектов в машинном обучении — это возможность обращения операторов.

Обращение операторов — это метод решения обратных задач, когда известен результат оператора, но неизвестны исходные данные. В контексте машинного обучения, это означает, что компьютер может использовать обратный оператор для нахождения исходных данных на основе уже имеющихся результатов. Это очень важно для обучения и оптимизации алгоритмов машинного обучения.

Существует множество методов обращения операторов, включая методы спектрального анализа, методы сжатия данных и методы оптимального управления. Некоторые из них успешно применяются в машинном обучении, например, алгоритм обратного распространения ошибки в нейронных сетях.

Однако, обращение операторов является сложной задачей в общем случае, и успешное применение алгоритмов машинного обучения достигается только путем тщательного анализа и предварительной обработки данных.

Примеры решения обратных задач в различных областях науки и техники

Решение обратных задач — это важный процесс в различных областях науки и техники. Ниже перечислены лишь некоторые примеры:

• Медицина. В области медицины обратные задачи позволяют получать информацию о внутренних структурах организма. Например, метод Монте-Карло применяется для расчета скрытых параметров эластичности ткани при обнаружении злокачественных опухолей.
• Геофизика. Некоторые обратные задачи в геофизике помогают определять свойства подземных коллекторов. Они основываются на моделировании потока жидкости в природных пористых средах, таких как нефтегазовые месторождения.
• Финансы. Решение обратной задачи вероятности в финансах позволяет устанавливать уровень риска и прибыли в различных инвестиционных портфелях. От прогнозирования надежности кредиторов до оптимизации дохода инвесторов, эти методы имеют широкие приложения в бизнесе.
• Компьютерное зрение. В компьютерном зрении обратные задачи играют важную роль в поиске и распознавании объектов на изображениях. Использование методов искусственного интеллекта и обработки изображений помогает достичь высокой точности.
• Физика. В физике обратные задачи могут использоваться для моделирования физических явлений на макроскопическом и микроскопическом уровнях. Например, идентификация параметров в модели маятника поможет понять поведение этой системы.

Это лишь некоторые примеры применения решения обратных задач в различных областях науки и техники. Но независимо от области, обратные задачи являются мощным инструментом для получения новых знаний и разработки новых технологий.

Перспективы и будущее развития методов решения обратных задач

Современный мир постоянно развивается и изменяется, требуя от нас развития и изменения научных методов и подходов для решения сложных задач. В области обратных задач мы можем ожидать появления новых и улучшенных методов решения, а также развития существующих.

Одно из направлений развития методов решения обратных задач — это использование машинного обучения и искусственного интеллекта. Учитывая то, как быстро эти области развиваются, мы можем предвидеть, что в ближайшие годы значительная часть задач будет решаться именно с помощью этих технологий.

Также важным направлением развития методов решения обратных задач является разработка новых алгоритмов. Ученые уже работают над созданием новых и эффективных методов решения, которые могут решать задачи, которые невозможно решить с помощью существующих методов.

Еще одним важным направлением является совмещение и объединение различных методов. Комбинирование методов решения обратных задач может привести к новым и более эффективным подходам.

В целом, будущее методов решения обратных задач выглядит весьма перспективным. С появлением новых технологий и новых исследований мы можем ожидать, что сможем решить даже еще более сложные задачи и обеспечить инновационный прогресс во многих областях.

Выводы: что нужно знать при решении обратной задачи в математике?

1. Определите цель решения обратной задачи. Прежде, чем начать решать обратную задачу, необходимо понимать, какие именно вопросы необходимо решить и какие данные будут необходимы для этого.

2. Используйте математические методы для анализа данных. Решение обратной задачи часто связано с анализом большого объема данных. Математические методы могут помочь обработать данные и вывести из них нужную информацию.

3. Используйте моделирование для проверки решения. Важно не только получить решение, но и проверить его на корректность и точность. Моделирование может помочь проверить решение на типичных сценариях и найти ошибки.

4. Не забывайте о неопределенности данных. В решении обратной задачи может быть множество неизвестных факторов и неопределенностей в данных. Важно учитывать этот факт и выбирать методы решения, которые учитывают неопределенность.

5. Используйте современные технологии и программное обеспечение. Современные технологии и программное обеспечение могут помочь ускорить и упростить процесс решения обратной задачи. Не стесняйтесь использовать их, если это возможно.

В итоге, решение обратной задачи в математике – это сложный и многогранный процесс. Однако, правильный подход и использование современных инструментов могут существенно облегчить задачу и привести к точным и эффективным результатам.