Как решать 15 задание ОГЭ по математике: подробный гайд

Хотите узнать, как решать 15 задание по математике на ОГЭ? Наша статья поможет вам разобраться в этой задаче и дать полезные советы для успешной сдачи ОГЭ по математике.

ОГЭ по математике является одним из самых ответственных испытаний для школьников 9-го класса. Кроме того, 15-ое задание является одним из самых сложных и требует от ученика не только знания основ математики, но и логической мысли.

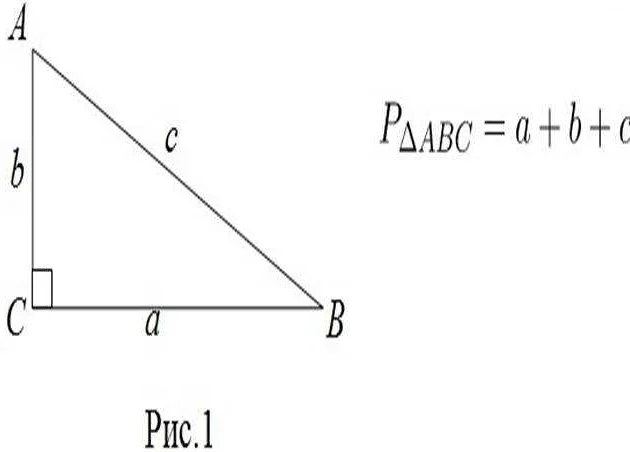
Задание состоит из двух частей, и в первой части необходимо найти среднее арифметическое двух чисел. Во второй части нужно вычислить периметр треугольника, зная только длины трех его сторон. Определенно, выполнение этой задачи может вызвать у ученика затруднения, но с правильной стратегией и подготовкой, он сможет успешно решить ее.

В статье мы рассмотрим подробную методику решения 15-ого задания ОГЭ по математике и предоставим различные примеры решений. Для тех, кто готовится к экзамену, это будет полезным материалом, который поможет справиться с этой трудной задачей и добиться высоких результатов на ОГЭ.

ОГЭ по математике: Как решать 15-ое задание

15-ое задание на ОГЭ по математике является одним из наиболее сложных заданий из всего списка. Оно проверяет умение ученика решать задачи на поиск площади фигуры.

Для решения этой задачи необходимо хорошо понимать основы геометрии, а также знать формулы для расчета площади различных фигур. В задаче могут быть приведены несколько величин, которые необходимо использовать для дальнейших расчетов.

Если вы столкнулись с трудностями при решении этой задачи, не отчаивайтесь. Во-первых, попытайтесь прочитать условие задачи несколько раз и определить, какие данные в нем содержатся. Во-вторых, используйте знания, полученные на уроках математики и геометрии, чтобы решить задачу.

• Шаг 1: Понять условие задачи.
• Шаг 2: Определить известные и неизвестные величины.
• Шаг 3: Использовать формулы для расчета неизвестных величин.
• Шаг 4: Составить ответ на задачу.

Решение 15-ого задания на ОГЭ по математике может быть сложным, однако, при наличии достаточного количества начальных знаний и умений, оно выполнимо. Главное — не отчаиваться и уверенно идти к цели.

Видео по теме:

Понимание условия задания

Чтобы решить 15-ое задание по математике на ОГЭ, необходимо сначала внимательно прочитать условие задания. Это поможет понять, какое решение нужно найти и какой метод использовать.

Особое внимание следует уделить формулировкам и математическим обозначениям. Если что-то не понятно, можно воспользоваться толковым словарем или обратиться к учителю за помощью.

Также очень важно обратить внимание на ограничения, которые указаны в условии задания. Например, ограничения на значения переменных, диапазон чисел и т.д. Невнимательное отношение к ограничениям может привести к неверному ответу.

Иногда в условиях заданий можно найти полезные подсказки, которые помогут решить задание проще и быстрее. Например, формулы, определения или конкретные примеры.

Важно запомнить, что в ОГЭ по математике задания могут быть довольно разнообразными. Поэтому при решении нужно быть готовым к неожиданным ситуациям и использовать все имеющиеся знания и навыки.

Разбор типичных ошибок

Задание №15 на ОГЭ по математике — задание на логику и понимание текстовых задач. Часто ошибки связаны не с математическими знаниями, а со внимательностью и навыками работы с текстом. Рассмотрим некоторые типичные ошибки и способы их избежания.

1. Неправильное понимание условия задачи

Перед тем как начать решать задачу, нужно внимательно прочитать условие, выяснить все детали и условия. Нередко ошибки возникают из-за неправильного понимания условия задачи.

• При чтении задачи выделяйте ключевые слова и фразы, которые помогут понять, что требуется вычислить, сколько и что известно, и как соотносятся все элементы задачи.
• Не перепутайте данные в условии задачи и не оставьте ненужные детали в решении.

2. Неверное использование математических формул

Математические формулы помогают нам решать задачи, но их неверное применение может привести к ошибкам.

• Убедитесь, что понимаете значения всех переменных в формуле и запомните формулы наизусть.
• Не забывайте, что правильное решение задачи должно соответствовать ответу в соответствии с условиями задачи.

3. Неправильный переход от слова к действию

В текстовых задачах иногда сложно увидеть, какую математическую операцию нужно выполнить.

• Прежде чем начинать решать задачу, разберитесь, какому виду задачи она принадлежит: поисковая, оптимизационная, квантификационная или определение соотношения.
• Попробуйте обнаружить сокращения, которые можно сделать, и определите, какой метод решения является лучшим.

Следуйте этим советам, и вы сможете избежать типичных ошибок в решении задач на ОГЭ по математике. Внимательность и логическое мышление помогут вам лучше понять условия, правильно применять формулы и убедиться в правильности решения.

Вопрос-ответ:

Как правильно формулировать гипотезу в 15-ом задании ОГЭ по математике?

Гипотеза должна быть ясной, конкретной и сформулированной в математическом языке. Желательно использовать знаки математических операций и математические функции. Например, «Если x^2 + 4x + 3 = 0, то x_1 = -1, x_2 = -3», где x_1 и x_2 — корни квадратного уравнения.

Как проверить гипотезу в задании?

Для проверки гипотезы нужно произвести несколько расчетов, используя данные условия задачи. Если результаты расчетов совпадают с предположениями, можно считать гипотезу верной. Если же результаты расходятся, гипотеза нуждается в дополнительных исследованиях или корректировке.

Какой подход лучше выбрать для решения 15-ого задания ОГЭ по математике?

Лучший подход — делать все пошагово и не торопиться. Сначала внимательно прочитать условие задачи и выделить ключевые моменты. Затем сформулировать гипотезу и проверить ее. Если гипотеза верна, можно приступать к построению доказательства. Если гипотеза не верна, нужно подумать, в чем была допущена ошибка и попытаться исправить ее.

Какие математические знания должны быть подготовлены учениками для успешного решения 15-го задания ОГЭ по математике?

Ученикам следует знать основы алгебры и геометрии, уметь работать с уравнениями и неравенствами, использовать геометрические построения, определять функции. Также полезным будет знание теории чисел и графов. Все эти знания помогут при решении задачи и формулировании гипотезы.

Можно ли в 15-ом задании ОГЭ по математике использовать примеры?

Да, использование примеров может очень помочь в решении задачи и формулировании гипотезы. Однако примеры следует использовать с осторожностью и проверять гипотезу на всех возможных примерах, чтобы получить более общее и точное решение.

Как не терять концентрацию и не утомляться при решении 15-го задания ОГЭ?

Важно делать небольшие перерывы на отдых и разминку, чтобы не утомляться и сохранять концентрацию. Полезным будет также решать простые задачи, чтобы не терять связь с математикой и не сбиться с пути. Задачи можно выбирать из легкой математической литературы или из Интернета.

Как выучить формулы, которые нужны для решения 15-го задания ОГЭ?

Для запоминания формул нужно задавать себе частые вопросы, связанные с математическими областями, к которым относятся эти формулы. Например, «Как вычислить площадь круга?». Также полезно будет составлять свои собственные формулы и решать задачи, где эти формулы применяются.

Правила решения задач на графики

Решение задач на графики – это умение определить зависимость, составить уравнение и найти неизвестные значения при помощи графического изображения. Важно знать основные правила, чтобы успешно решать этот тип задач.

Правило 1: Четко определите оси координат и масштаб – они помогут вам более точно определить зависимость.

Правило 2: Найдите точки пересечения графика с осями координат. Это может помочь в определении основных параметров, например, коэффициента при x в уравнении графика.

Правило 3: Определите тип зависимости – прямая или кривая, монотонная или немонотонная. Это поможет составить уравнение графика.

Правило 4: Составьте уравнение графика, используя известные параметры. Учтите, что формула может отличаться в зависимости от типа зависимости.

Правило 5: Найдите неизвестные значения в уравнении, используя изображение графика и известные параметры. Это может помочь определить различные параметры, такие как коэффициент при x или y.

Помните, что ключевым в решении задач на графики является внимательность и точность. Следуйте основным правилам, чтобы успешно решать задачи и достигать высоких результатов на экзаменах и тестах.

Правила решения задач на таблицы и диаграммы

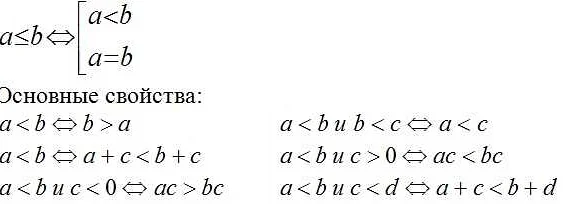
Задачи на таблицы и диаграммы в ОГЭ по математике могут быть разных типов, но общие правила решения таких задач можно выделить.

1. Тщательно прочитайте постановку задачи

Первым шагом при решении задач на таблицы и диаграммы необходимо тщательно прочитать постановку задачи. Уделите внимание всем деталям, таким как единицы измерения, количественные значения, период времени, наименования категорий и т.д.

2. Анализируйте предоставленные данные

После того, как вы прочитали постановку задачи, проанализируйте предоставленную информацию. Обратите внимание на все значения, представленные в таблице или диаграмме, примените соответствующие формулы, если это необходимо, и сделайте выводы.

3. Используйте логическое мышление

Для успешного решения задач на таблицы и диаграммы нужно использовать логическое мышление. Анализируйте предоставленные данные и делайте выводы на основе этих данных. Например, если задача спрашивает о тенденциях, которые можно увидеть на диаграмме, обращайте внимание на направление графиков, отклонения, тренды и т. д.

4. Не забывайте об оформлении решения

Наконец, не забывайте об оформлении вашего решения. Пишите пошаговое объяснение, как вы пришли к ответу. Если необходимо, используйте таблицы, диаграммы и формулы, чтобы проиллюстрировать свой подход. Проверьте свой ответ на правильность и достаточность информации.

Следуя этим простым правилам, вы сможете успешно решать задачи на таблицы и диаграммы на ОГЭ по математике.

Правила решения задач на связку геометрических фигур

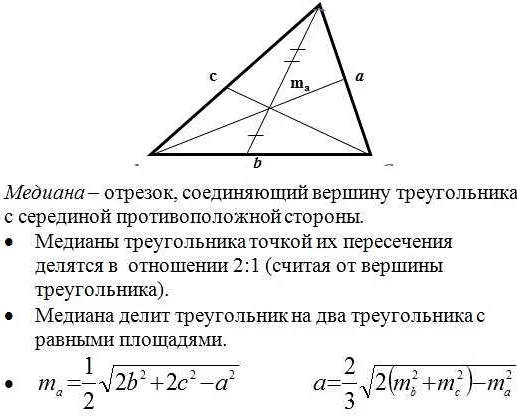
Решение задач по геометрии, которые включают в себя связку различных фигур, требует определенных правил и навыков. Важно не только знать свойства геометрических фигур, но и уметь правильно их «сочетать» между собой.

Правило 1. Вначале необходимо проанализировать задачу и выделить все геометрические фигуры, которые в ней присутствуют. Затем с помощью геометрических свойств определить, какие стороны, углы и диагонали эти фигуры имеют.

Правило 2. Учитывая все геометрические данные, следующим шагом является построение новых фигур, основанных на связке имеющихся. Обычно в задачах требуется построить параллелограммы, треугольники, квадраты и другие фигуры.

Правило 3. После построения новых геометрических фигур нужно воспользоваться свойствами сходных и равных фигур, для того чтобы определить искомые значения.

Правило 4. Если в задаче присутствует несколько связок геометрических фигур, следует выполнять действия последовательно, начиная с первой связки и продвигаясь далее.

Важно понимать, что задачи на связку геометрических фигур могут быть очень разнообразными и требовать различных подходов к решению. Однако, если вы хорошо понимаете свойства геометрических фигур и умеете правильно их сочетать между собой, вы сможете решать любые задачи и получать высокие баллы на экзаменах.

Правила решения задач на связку графиков функций

1. Анализируйте условие: в задаче обычно даны две функции, а также определен интервал значений аргумента функций. Обязательно выделите ключевые фразы и данные, которые могут помочь в решении задачи.

2. Постройте графики функций: на основе данных условия нарисуйте графики функций в одной системе координат. Правильность построения графиков очень важна, так как только при корректном построении можно найти искомые значения.

3. Определите точки пересечения: найдите точки пересечения графиков функций. Это можно сделать, решив уравнения системы функций. Точки пересечения помогут дать ответ на задачу, например, найти значение аргумента функции в заданных условиях.

4. Найдите точки экстремума: при корректном построении графиков функций можно обнаружить точки экстремума. Это позволит определить максимальное или минимальное значение функции в заданных условиях.

5. Проанализируйте полученные результаты: после определения точек пересечения и экстремумов, проанализируйте полученные результаты и ответьте на поставленный вопрос в задании. Не забывайте проверить полученный ответ на соответствие условиям задачи.

Правильный подход к задачам с условными обозначениями

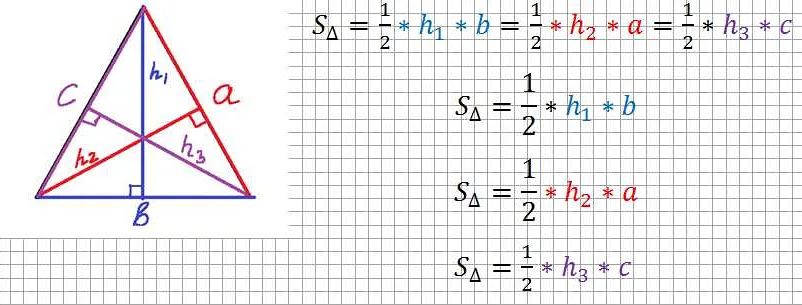
Задачи с условными обозначениями в ОГЭ по математике могут вызвать затруднения у многих учащихся, но с правильным подходом к их решению, они перестают быть страшными.

Первым шагом к решению задач с условными обозначениями является определение смысла каждого условного обозначения. Необходимо четко понимать, что оно означает и какое значение имеет в задаче.

Далее следует составление таблицы истинности для каждого условного обозначения, где перечисляются все возможные значния обозначения и результаты, которые они приводят. Это помогает определить правильный ответ на вопрос, заданный в условии задачи.

Важным аспектом при решении задач с условными обозначениями является внимательное чтение условия. Необходимо быть внимательным к тонкостям текста, таким как слова «всегда», «никогда», «некоторые», «все» и так далее. Эти слова могут точно указать на ответ на вопрос задачи.

В итоге, правильный подход к задачам с условными обозначениями заключается в хорошем понимании смысла каждого условного обозначения, составлении таблицы истинности и внимательном чтении условия. При правильном выполнении этих шагов, решение задачи становится проще и понятнее.

Методы решения задач с пропорциями и долями

Решение задач с пропорциями и долями может показаться сложным на первый взгляд, но на самом деле это основывается на простых математических операциях.

Для начала, необходимо понимать, что пропорция — это соотношение двух или более величин. Пропорции могут быть прямые или обратные. Для решения прямых пропорций, необходимо умножать или делить все величины на одно и то же число. Для решения обратных пропорций, необходимо умножать или делить одну величину на другую.

Допустим, у нас имеется пропорция: a:b = c:d. Мы знаем значение переменной «a» и хотим найти значение «b». Для этого необходимо умножить значение переменной «c» на «a», и разделить результат на «d». Таким образом, мы получаем значение переменной «b».

Доли это еще один важный аспект при решении задач по математике. В них необходимо определить, сколько процентов из общей суммы относится к тому или иному объекту. Для этого необходимо разделить сумму на количество объектов, а затем умножить результат на процент, который нужно найти.

Например, имеется 500 рублей и 5 монет, и нужно найти долю каждой монеты в общей сумме. Для этого необходимо разделить сумму на количество монет (500 руб. / 5 монет = 100 руб. за 1 монету). Для нахождения доли каждой монеты, нужно умножить 100 руб. на процентное значение доли монеты.

В целом, решение пропорций и долей требует простых математических операций, но требует от студентов внимательности и аккуратности при работе с числами и значениями.

Понимание основных понятий в задачах на статистику

Решение задач на статистику часто требует понимания основных понятий, которые используются в этой области математики. Одним из таких понятий является выборка.

Выборка — это часть генеральной совокупности, на которую проводятся исследования. Извлечение выборки осуществляется с целью получения информации о генеральной совокупности.

Для оценки характеристик генеральной совокупности, например, среднего значения или дисперсии, используются статистические показатели. Среди таких показателей наиболее часто используемые это выборочное среднее и выборочная дисперсия.

Выборочное среднее — это среднее арифметическое всех значений в выборке. Оно показывает среднее значение параметра в выборке.

Выборочная дисперсия — это мера разброса значений в выборке относительно выборочного среднего. Она показывает, насколько сильно значения в выборке отличаются друг от друга.

При решении задач на статистику также используется понятие доверительного интервала. Доверительный интервал — это интервал значений, в котором с некоторой вероятностью находится истинное значение параметра генеральной совокупности.

Важно понимать, что при решении задач на статистику необходимо учитывать условия задачи, такие как уровень значимости и размер выборки. Неправильные предположения могут привести к неправильным результатам.

Основные методы решения задач на вероятность

Вероятность – это существенная часть математической теории, которая применяется для анализа случайных событий. Решение задач на вероятность – это ключевой элемент в ОГЭ по математике. Самые распространенные методы их решения – это метод полной вероятности, метод условной вероятности и метод Байеса.

Метод полной вероятности: данный метод используется в тех случаях, когда необходимо выяснить вероятность наступления событий в последовательности. Для его применения нужно знать вероятность наступления каждого из событий и их поведение в каждой ситуации.

Метод условной вероятности: данный метод используется при изучении случайных событий, когда их возможность зависит от других значимых факторов. Он позволяет вычислить вероятность наступления события при условии, что уже наступило базовое событие.

Метод Байеса: данный метод используется для вычисления вероятности наступления событий на основании уже имеющихся данных. Он позволяет оценить вероятность наступления событий на основании предыдущих исследований, как-то других источников информации.

Необходимые для решения задач на вероятность формулы можно найти в учебниках по математике или на специализированных сайтах в интернете. Помимо основных методов, для решения задач на вероятность могут использоваться и другие приемы, которые помогают ученикам более эффективно выполнять задания на данную тему.

1. Понимайте теорию;
2. Анализируйте задачу: четко сформулируйте условие, перечислите данные, запишите все, что дано в условии. Нужно понимать основные термины и определения;
3. Применяйте изученные формулы;
4. Вычисляйте результат и обязательно проверяйте его на корректность.

Решая задачи на вероятность, необходимо следить за правильностью расчетов и вовремя применять изученные методы. Подходя к решению задач на эту тему с усердием и упорством, вы сможете успешно справиться с этими заданиями на ОГЭ по математике.

Подходы к задачам на математические модели

Решение задач на математические модели требует особого подхода, который включает в себя несколько этапов. Начнем с формулировки самой задачи. Необходимо понять, какую именно модель нужно использовать, чтобы решить поставленную задачу.

Далее, необходимо провести анализ полученной модели, вычислить ее характеристики и оценить ее достоверность. Для этого используются специальные методы, например, метод Монте-Карло или методы статистического анализа данных.

После этого осуществляется решение самой задачи, используя полученную модель и вычисленные значения. Необходимо помнить, что решение всегда должно быть адекватным поставленной задаче, иначе результаты могут быть неверными.

Наконец, необходимо провести анализ полученных результатов и оценить их точность и достоверность. В случае необходимости, можно также провести чувствительность анализа, чтобы понять, какие параметры модели оказывают наибольшее влияние на результат.

Помните, что каждая задача имеет свои особенности и может требовать индивидуального подхода. Однако, правильное применение указанных методов и подходов к созданию математических моделей может помочь в решении практически любой задачи.