Что такое отношение в математике
Содержимое
Отношение в математике — это связь или соотношение между двумя или более элементами. Оно может быть представлено в виде графика, таблицы или множества упорядоченных пар. Отношения используются для анализа, классификации и представления данных в различных областях математики, таких как алгебра, геометрия и теория вероятностей.
Отношение – важное понятие в математике, которое используется для описания связей между элементами двух множеств. Оно позволяет установить, какие элементы одного множества соотносятся с элементами другого. Отношение может быть представлено различными способами и иметь различные свойства.
Одним из основных свойств отношений является рефлексивность. Если каждый элемент первого множества связан с самим собой, то отношение называется рефлексивным. Например, отношение «больше или равно» между числами является рефлексивным, так как каждое число больше или равно самому себе.
Еще одним свойством отношений является симметричность. Если каждый элемент первого множества связан с элементом второго множества, то отношение называется симметричным. Например, отношение «равенство» между числами является симметричным, так как если число А равно числу В, то число В также равно числу А.
Кроме того, отношение может быть транзитивным. Если элемент первого множества связан с элементом второго множества, а элемент второго множества связан с элементом третьего множества, то элемент первого множества также будет связан с элементом третьего множества. Например, отношение «больше» между числами является транзитивным, так как если число А больше числа В, а число В больше числа С, то число А также будет больше числа С.
В математике существует множество примеров отношений, которые используются для решения различных задач. Например, отношение «принадлежит» может быть использовано для определения, принадлежит ли точка заданной фигуре. Отношение «сходится к» используется для определения предела функции. Отношение «делится на» позволяет определить, делится ли число на другое без остатка. Такие примеры отношений помогают математикам анализировать и описывать различные явления и связи в мире чисел и формул.
Понятие отношения
В математике отношение представляет собой связь или соотношение между двумя или более объектами. Оно позволяет определить, как один объект связан или зависит от другого объекта.
Отношение можно представить в виде таблицы, которая содержит пары значений или упорядоченных пар элементов. Каждая пара значений состоит из элемента из первого множества, называемого доменом отношения, и элемента из второго множества, называемого областью значений.
Отношение может быть представлено также в виде графа, где вершины представляют элементы из домена и области значений, а ребра представляют связи между этими элементами.
Отношения могут быть разных типов, например, функциональные или нефункциональные. Функциональное отношение означает, что каждому элементу из домена соответствует только один элемент из области значений. Нефункциональное отношение, наоборот, позволяет одному элементу из домена соответствовать несколько элементов из области значений.
Отношения могут также быть симметричными или асимметричными. Симметричное отношение означает, что если элемент A связан с элементом B, то элемент B также связан с элементом A. Асимметричное отношение, наоборот, означает, что если элемент A связан с элементом B, то элемент B не связан с элементом A.
Пример таблицы отношенияДоменОбласть значений
| A | 1 |
| B | 2 |
| C | 3 |
В данном примере в домене присутствуют элементы A, B и C, а в области значений — элементы 1, 2 и 3.
Типы отношений

В математике существует несколько типов отношений, которые определяются в зависимости от свойств элементов множеств, между которыми установлено отношение. Рассмотрим некоторые из них:
Тип отношенияОпределениеПример
| Рефлексивное | Каждый элемент множества A связан с самим собой. | Отношение «быть равным» на множестве натуральных чисел. |
| Симметричное | Если элемент A связан с элементом B, то элемент B связан с элементом A. | Отношение «быть параллельным» на множестве прямых. |
| Транзитивное | Если элемент A связан с элементом B и элемент B связан с элементом C, то элемент A связан с элементом C. | Отношение «быть предшествующим» на множестве событий. |
| Антисимметричное | Если элемент A связан с элементом B и элемент B связан с элементом A, то A и B — один и тот же элемент. | Отношение «быть подмножеством» на множестве. |
Это лишь некоторые из множества возможных типов отношений в математике. Каждый тип отношения имеет свои особенности и применение в различных областях математики.
Рефлексивные отношения

Выделяют два типа рефлексивных отношений:
1. Тривиальное рефлексивное отношение: в этом случае каждый элемент множества связан сам с собой единственным способом. Например, множество всех людей, у которых отношение «быть родителем» является тривиальным рефлексивным отношением, так как каждый человек является родителем самого себя.
2. Нетривиальное рефлексивное отношение: в этом случае каждый элемент множества связан сам с собой более чем одним способом. Например, множество всех чисел, у которых отношение «быть больше или равным» является нетривиальным рефлексивным отношением, так как каждое число больше или равно самому себе.
Рефлексивные отношения играют важную роль в математике и других областях науки, так как позволяют строить логические цепочки и доказывать различные утверждения и теоремы.
Симметричные отношения
Математически, если (а, b) является парой элементов, принадлежащих отношению R, то (b, a) также принадлежит отношению R.
Примером симметричного отношения может служить отношение «равно». Если А равно В, то В также равно А. Также, отношение «параллельно» между прямыми — симметричное отношение. Если прямая А параллельна прямой В, то прямая В также параллельна прямой А.
ОтношениеПример
| Равно | Если a = b, то b = a |
| Параллельно | Если прямая a параллельна прямой b, то прямая b параллельна прямой a |
Транзитивные отношения
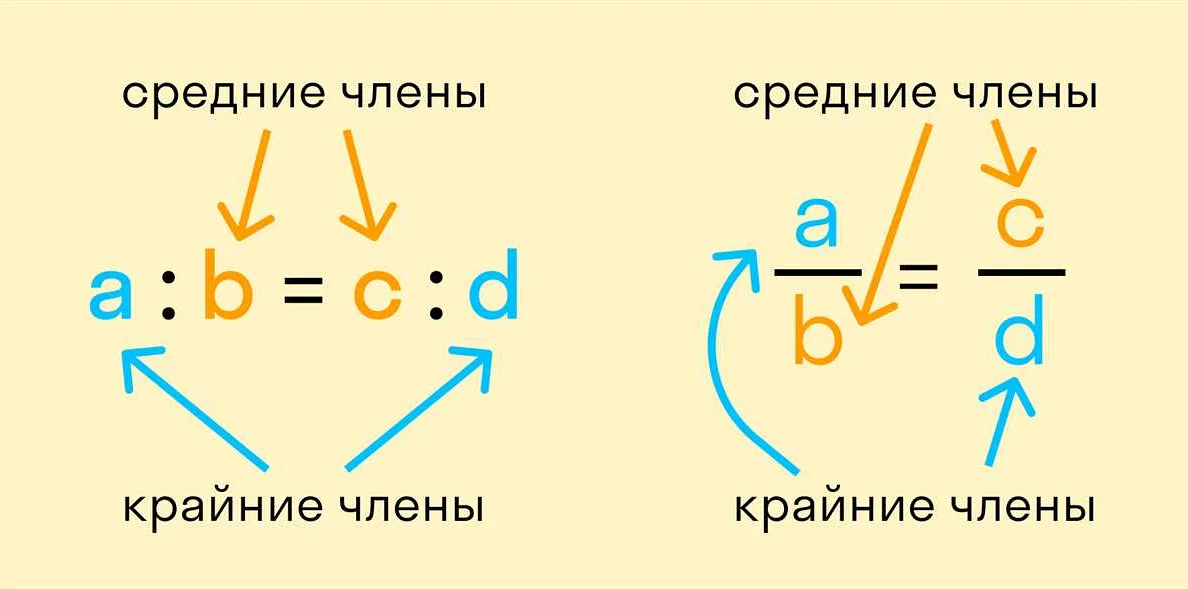
Таким образом, если в отношении R соотношение (a, b) и соотношение (b, c), то в отношении R также будет соотношение (a, c). Это свойство позволяет строить цепочки связей между элементами и устанавливать транзитивные связи.
Примером транзитивного отношения является отношение «больше» на множестве натуральных чисел. Если число a больше числа b, а число b больше числа c, то число a также будет больше числа c. Таким образом, отношение «больше» является транзитивным отношением.
Транзитивные отношения играют важную роль в математике и других областях, таких как графовая теория и теория отношений. Они позволяют анализировать связи между элементами и строить логические цепочки выводов.
ОтношениеТранзитивное?
| Равенство | Да |
| Больше | Да |
| Меньше | Да |
| Делится на | Да |
| Принадлежит | Да |
Эквивалентность и порядок
В математике существуют два важных понятия, связанных с отношением между элементами множества: эквивалентность и порядок.
Эквивалентность — это отношение между элементами множества, которое означает их равенство. Если элементы образуют эквивалентные классы, то они считаются равными друг другу по определенному критерию. Например, в множестве натуральных чисел, элементы, которые имеют одинаковый остаток при делении на 5, образуют эквивалентные классы. Эквивалентность может быть представлена с помощью таблицы, в которой указываются пары эквивалентных элементов.
КлассЭлементы
| [0] | 0, 5, 10, 15, … |
| [1] | 1, 6, 11, 16, … |
| [2] | 2, 7, 12, 17, … |
| [3] | 3, 8, 13, 18, … |
| [4] | 4, 9, 14, 19, … |
Порядок — это отношение между элементами множества, которое определяет, какой элемент больше или меньше. Порядок можно представить с помощью таблицы, в которой указываются пары элементов и их отношение (больше или меньше).
Элемент 1Элемент 2Отношение
| 1 | 2 | Меньше |
| 2 | 3 | Меньше |
| 3 | 4 | Меньше |
| 2 | 4 | Меньше |
| 4 | 1 | Больше |
Таким образом, эквивалентность и порядок — это два важных понятия в математике, которые помогают анализировать и сравнивать элементы множества.
Примеры отношений
Вот несколько примеров отношений:
ПримерОписание
| Отношение «больше» | Это отношение, которое устанавливается между двумя числами и означает, что одно число больше другого. |
| Отношение «равно» | Это отношение, которое устанавливается между двуми элементами и означает, что они равны друг другу. |
| Отношение «принадлежит» | Это отношение, которое устанавливается между элементом и множеством и означает, что элемент принадлежит множеству. |
| Отношение «подмножество» | Это отношение, которое устанавливается между двуми множествами и означает, что одно множество является подмножеством другого. |
Это лишь некоторые примеры отношений, с которыми вы можете столкнуться в математике. Важно помнить, что отношения играют важную роль в алгебре, геометрии и других разделах математики.
Применение отношений в математике и реальной жизни
Отношения играют важную роль не только в математике, но и в реальной жизни. Они используются для описания различных связей, сравнений и взаимодействий между объектами.
В математике отношения широко применяются в алгебре, геометрии, теории графов и других разделах.
Одним из основных применений отношений в математике является определение и изучение функций. Функция — это особый вид отношения между множествами, где каждому элементу первого множества соответствует ровно один элемент второго множества. Функции используются для описания зависимостей между переменными и представляют собой мощный инструмент для моделирования и анализа различных явлений.
Отношения также применяются в реальной жизни. Например, они используются для описания социальных сетей. В социальных сетях каждый человек может быть связан с другими людьми через различные отношения, такие как дружба, родство, знакомство и т. д. Анализ отношений в социальных сетях позволяет выявлять группы людей с общими интересами, изучать влияние одного человека на других и прогнозировать распространение информации или вирусных заболеваний.
Другим примером применения отношений в реальной жизни является моделирование сетей транспортных маршрутов. Отношения между различными пунктами назначения позволяют определить оптимальные маршруты и расчет времени пути. Это особенно важно для организации грузоперевозок и пассажирского транспорта.
Таким образом, отношения являются неотъемлемой частью математики и науки в целом, а их применение в реальной жизни позволяет решать различные задачи и улучшать нашу жизнь.
Видео по теме:
Что такое отношение в математике?
В математике отношение — это понятие, которое описывает связь между двумя объектами или событиями.
Какие основные виды отношений существуют в математике?
В математике существует несколько основных видов отношений, таких как: равенство, порядок, эквивалентность, функция.
Что такое эквивалентность в отношениях?
Эквивалентность — это отношение между объектами, при котором они считаются эквивалентными, то есть имеют одинаковые свойства или характеристики.
Какие примеры отношений можно привести?
В качестве примеров отношений можно привести отношение «больше», «меньше» или «равно» в порядке чисел, отношение «является частью» в множествах, отношение «является родителем» в семейных деревьях и другие.
Какие свойства может иметь отношение?
Отношение может иметь различные свойства, такие как рефлексивность, симметричность, транзитивность и др.
Что такое отношение в математике?
Отношение в математике — это связь или соответствие между элементами двух множеств. Оно выражается в виде пары значений, где первый элемент принадлежит одному множеству, а второй элемент — другому множеству. Отношение может быть представлено графически, таблицей или формулой.




Математика — это одна из тех наук, которая способна раскрывать перед нами мир совершенства и логики. Отношение в математике — это одно из важнейших понятий, которое позволяет выявить связь между двумя числами или объектами. Ведь в реальной жизни мы очень часто сталкиваемся с ситуациями, где нужно сравнивать и оценивать разные величины. Например, можно рассмотреть отношение между двумя числами, такие как 4 и 8. В данном случае мы можем сказать, что число 8 вдвое больше числа 4, то есть отношение между ними можно записать как 8:4=2. Это означает, что величина числа 8 в два раза превышает величину числа 4. Еще один пример — отношение между двумя группами объектов. Представим, что у нас есть группы красных и синих шаров. Если в красной группе 10 шаров, а в синей — 5, то отношение между ними можно записать как 10:5=2. Это означает, что в красной группе шаров в два раза больше, чем в синей. Отношения в математике помогают нам понять взаимосвязь между объектами и оценить их относительные величины. Они являются основой для многих других математических понятий и помогают решать сложные задачи. Поэтому освоение этой темы важно для понимания и применения математики в повседневной жизни.
Хочу сказать, что статья очень понятно и доступно объясняет основные понятия отношения в математике. Я всегда думала, что математика слишком сложна и непонятна, но благодаря этой статье я смогла разобраться в том, что такое отношение и как оно работает. Мне понравилось, что автор привела примеры, которые помогли мне лучше понять материал. Например, объяснение отношения «больше» и «меньше» с помощью чисел было очень наглядным и понятным. Также автор дал примеры отношений в реальной жизни, что помогло мне увидеть, как отношения применяются в повседневной жизни. Мне также понравилось, что статья была структурирована и легко читалась. Автор четко разделила основные понятия, объяснила каждое из них и дала примеры. Это помогло мне удерживать весь материал в голове и не запутаться. В целом, статья была очень полезной и понятной. Теперь я лучше понимаю, что такое отношение в математике и как его можно применять. Благодаря этой статье, я чувствую себя более уверенной в своих знаниях и готова применить их на практике. Спасибо автору за такую интересную и понятную статью!
Статья очень полезна и информативна. Математика всегда казалась мне сложной и непонятной, но благодаря этой статье я начинаю осознавать ее важность и применимость в повседневной жизни. Например, понятие отношения помогает мне лучше понимать взаимосвязи между различными величинами и оценивать их важность. Теперь я понимаю, что отношение — это нечто большее, чем просто математический термин. Это инструмент, который позволяет анализировать и объяснять мир вокруг нас. Я особенно заинтересовалась примерами из реальной жизни, которые автор привел в статье. Например, отношение между скоростью и временем позволяет определить расстояние, которое пройдет автомобиль за определенное время. Это простой пример, но он помогает увидеть практическую применимость математики в нашей жизни. Очень важно, что автор объяснил основные понятия отношения, такие как эквивалентность, подобие и порядок. Теперь я понимаю, что отношение может быть не только числовым, но и геометрическим или логическим. Это расширяет мой взгляд на математику и позволяет мне увидеть ее в различных областях. В целом, статья очень доступно и понятно излагает основные понятия отношения в математике. Я благодарна автору за его старания и надеюсь увидеть еще больше примеров и объяснений в следующих статьях.