Что такое отношение величин в математике 6 класс

Отношение величин в математике 6 класс – это способ сравнения двух или более значений, установление их взаимосвязи и определение, насколько одна величина больше или меньше другой. Учебная статья расскажет о базовых понятиях и примерах отношений величин в 6 классе математики.

В математике одним из основных понятий является отношение величин. Отношение – это связь между двумя или более величинами, которая позволяет сравнивать их между собой. Оно может быть выражено с помощью различных математических знаков и символов.

Одним из примеров отношения величин является сравнение чисел. Например, если мы сравниваем числа 3 и 5, то можем сказать, что 5 больше 3. Здесь мы используем знак «больше» для выражения отношения между этими числами.

Еще одним примером отношения величин может быть сравнение длин двух отрезков. Если один отрезок длиннее другого, то мы можем сказать, что первый отрезок больше второго. Здесь мы снова используем знак «больше», чтобы выразить отношение между этими отрезками.

Отношение величин играет важную роль в математике, поскольку позволяет сравнивать и упорядочивать различные величины. Оно помогает нам определить, какая величина больше или меньше, и решать различные задачи на сравнение и упорядочивание величин.

В заключение, отношение величин является основным понятием в математике и используется для сравнения и упорядочивания различных величин. Оно выражается с помощью математических знаков и помогает решать задачи на сравнение и упорядочивание величин.

Основные понятия математики

Число — основной объект изучения в математике. В математике существуют различные виды чисел, такие как натуральные, целые, рациональные и дробные числа. Числа можно складывать, вычитать, умножать и делить.

Форма — геометрическая фигура, ограниченная линиями или поверхностями. Формы могут быть плоскими (круг, треугольник) или объемными (шар, параллелепипед).

Пространство — природное или искусственное устройство, обладающее трехмерными размерами (длина, ширина, высота). Пространства могут быть геометрическими (трехмерное пространство) или абстрактными (пространство решений).

Измерение — процесс определения количественного значения величин, например длины, площади, объема. Измерение позволяет сравнивать и классифицировать объекты по их свойствам.

Изображение — графическое представление объектов и их свойств с помощью геометрических фигур, чисел, графов и диаграмм. Изображения используются в математике для визуализации и анализа данных.

Знание основных понятий математики позволяет развивать логическое мышление, решать задачи и применять математические знания в повседневной жизни.

Отношение величин: основные понятия

В математике понятие «отношение величин» используется для описания связи между двумя или более числами или величинами. Отношение можно представить в виде дроби или соотношения, которое показывает, как одна величина связана с другой.

В отношении величин выделяют несколько основных понятий:

1. Частное: это результат деления одной величины на другую. Например, если имеется отношение величин 9 к 3, то частное будет равно 3 (9 ÷ 3 = 3).
2. Пропорция: это особое отношение, при котором частное двух величин равно частному двух других величин. Например, если имеется отношение величин 6 к 3 и 12 к 6, то это пропорция (6 ÷ 3 = 12 ÷ 6).
3. Процент: это специальное отношение, которое выражает одну величину как процент другой величины. Например, если имеется отношение величин 25 к 100, то это может быть выражено как 25% (25 ÷ 100 = 0.25).
4. Отношение равенства: это отношение, при котором две величины или выражения равны друг другу. Например, если имеется отношение величин 3 + 4 к 2 × 4, то это отношение равенства (3 + 4 = 2 × 4).

Знание основных понятий отношения величин позволяет решать разнообразные задачи и применять математические операции для анализа и сравнения чисел и величин.

Отношение величин в математике 6 класс: предмет изучения

Отношение величин можно представить с помощью дробей или соотношений. Например, если имеется две величины A и B, и их отношение равно 2:3, то это означает, что для каждых 2 единицы величины A приходится 3 единицы величины B.

Изучение отношения величин позволяет решать задачи, связанные с пропорциями, сравнением и преобразованием величин. Оно также помогает развить навыки логического мышления, анализа и решения проблем.

Примеры задач, связанных с отношением величин, включают расчеты процентного соотношения, определение среднего арифметического и решение задач на пропорциональное деление.

Изучение отношения величин в 6 классе является базовым для дальнейшего изучения математики и применения ее в повседневной жизни.

Отношение величин в математике 6 класс: классификация

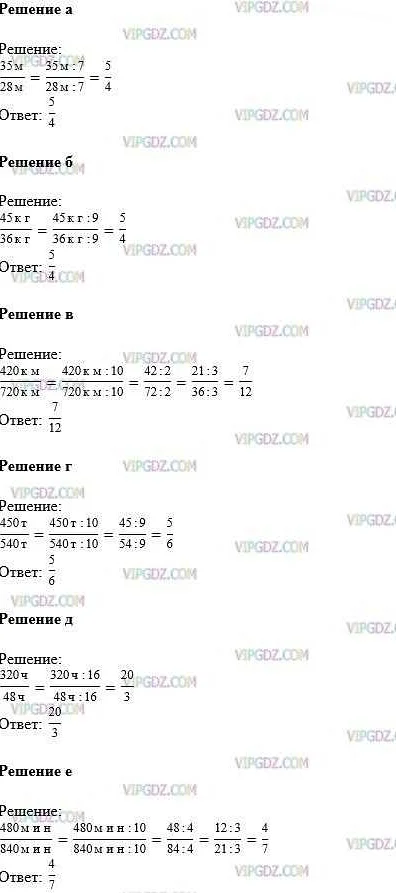
Отношение величин можно классифицировать на следующие типы:

1. Равенство: две величины считаются равными, если они полностью совпадают. Например, 3 + 4 и 7 являются равными величинами.

2. Неравенство: две величины считаются неравными, если они отличаются друг от друга. Например, 5 и 8 являются неравными величинами.

3. Больше: одна величина считается больше другой, если она превосходит ее по значению. Например, 9 больше 6.

4. Меньше: одна величина считается меньше другой, если она меньше ее по значению. Например, 2 меньше 7.

5. Больше или равно: одна величина считается больше или равной другой, если она либо превосходит ее по значению, либо равна ей. Например, 5 больше или равно 5.

6. Меньше или равно: одна величина считается меньше или равной другой, если она либо меньше ее по значению, либо равна ей. Например, 3 меньше или равно 3.

Знание и понимание этих классификаций отношения величин в математике 6 класса помогает учащимся анализировать и решать различные задачи, связанные с сравнением и классификацией величин.

Отношение величин в математике 6 класс: примеры

Рассмотрим несколько примеров:

1. Прямая пропорциональность. В этом случае, если одна величина увеличивается, то и другая величина также увеличивается, и они изменяются в одинаковой пропорции. Например, если мы изучаем зависимость между временем и расстоянием, то при увеличении времени в два раза, расстояние также увеличивается в два раза.

2. Обратная пропорциональность. В этом случае, если одна величина увеличивается, то другая величина уменьшается, и они изменяются в обратной пропорции. Например, если мы изучаем зависимость между скоростью и временем, то при увеличении скорости в два раза, время уменьшается в два раза.

3. Равенство. В этом случае, две величины равны друг другу. Например, если имеем уравнение 2x + 5 = 15, то значением переменной x будет 5.

4. Неравенство. В этом случае, одна величина больше или меньше другой. Например, если имеем неравенство 2x + 3 > 10, то значением переменной x может быть любое число, большее 3.

Все эти примеры отношений величин помогают нам понять и описать зависимости между различными величинами и решать математические задачи.

Значение отношения величин в повседневной жизни

Например, отношение величин может быть использовано для оценки пути, который нужно пройти от одной точки до другой. Мы можем сравнить расстояние между двумя городами и выбрать самый короткий путь.

Отношение величин также может быть полезным при покупке товаров. Мы можем сравнить цены на разные товары и выбрать наиболее выгодное предложение.

Кроме того, отношение величин может быть использовано для оценки времени. Например, мы можем сравнить время, затраченное на выполнение различных задач, и определить, какую задачу следует выполнить в первую очередь.

В повседневной жизни мы постоянно сталкиваемся с ситуациями, которые требуют сравнения и оценки различных величин. Знание и понимание отношения величин позволяет нам принимать более обоснованные и рациональные решения.

Выводы

В данной статье мы рассмотрели понятие отношения величин в математике и привели несколько примеров.

Отношение величин может быть представлено в виде дроби, где числитель и знаменатель обозначают соответствующие величины. Числитель показывает, сколько раз одна величина содержится в другой. Знаменатель показывает, во сколько раз одна величина больше или меньше другой.

Мы также рассмотрели различные виды отношений: пропорциональность, обратная пропорциональность и непропорциональность. В пропорциональных отношениях одна величина меняется пропорционально другой. В обратно пропорциональных отношениях одна величина меняется обратно пропорционально другой. В непропорциональных отношениях нет постоянного соотношения между величинами.

Понимание отношения величин позволяет нам анализировать различные ситуации и решать задачи, связанные с пропорциональностью и обратной пропорциональностью. Работа с отношениями также помогает нам лучше понимать мир вокруг нас и применять математические знания в повседневной жизни.

Успехов в изучении отношений величин!

Видео по теме:

Что такое отношение величин в математике?

Отношение величин – это сравнение двух чисел или величин, выраженное в виде отношения или дроби. Оно позволяет определить, во сколько раз одна величина больше или меньше другой.

Как можно выразить отношение величин в математике?

Отношение величин можно выразить с помощью отношения или дроби. Например, если одно число в 3 раза больше другого, то отношение будет 3:1 или дробь 3/1.

Зачем нужно понимать отношение величин в математике?

Понимание отношения величин в математике помогает сравнивать и анализировать различные числа и величины. Это важный навык при решении задач, построении графиков и анализе данных. Отношение величин также позволяет делать выводы о пропорциональности и изменениях между величинами.